Решение уравнений с помощью систем
 Скачать 45.09 Kb.
|
| 11 класс. Урок алгебры и начала математического анализа. Тема «Решение уравнений с помощью систем». Цели урока: закрепить навыки и умения учащихся при решении уравнений с помощью систем, повысить мотивацию учащихся к обучению, расширить представление учащихся о применении логарифмов в различных областях естествознания, определить прочность знаний, умений, навыков при решении уравнений; развивать логическое мышление, умение анализировать, оперировать полученными знаниями и навыками, выделять главное, обобщать; воспитание познавательной активности, культуры общения, ответственности. Девиз урока: «Ум - хорошо, а два - лучше». Эпиграф урока: «Химия - правая рука физики, математика - ее глаз» М.В Ломоносов Ход урока 1.Сообщение темы и целей урока. Для этого нужно прочитать и исключить лишние слова: еынпобод (подобные), чогменлон (многочлен), ярамяп (прямая), циэфокфните (коэффициент), уеранвени (уравнение), реконь (корень), стесмаи (система). И так тема урока «Решение уравнений с помощью систем». Эпиграфом урока слова М.В Ломоносова «Химия – правая рука физики, математика – ее глаз». Давайте вспомним в каком году исполнилось 300 лет со дня рождения М.В Ломоносова? (Учащиеся разделены на 2 группы, каждую группу возглавляет капитан). Капитаны команд получают задания . Найти значения выражения 335у+1=? Если 2х2-12х+3у=0 имеет 1 корень.(Ответ: 2011 г) Пока учащиеся определяют год юбилея, другой ученик делает сообщение о творческой деятельности М.В Ломоносова. 2. «А вы знаете, что…»(Плакат). Многочлен по – другому можно назвать полином. Одночлен – моном. Двучлен – бином. Трехчлен – трином. Учитель: Ребята, мы с вами изучили свойства показательной функции, понятие логарифма и его свойства, научились решать показательные и логарифмические уравнения. А теперь я предлагаю рассмотреть в каких областях наук возможно практическое применение полученных вами знаний II. Историческая справка. (7 мин.) Трое учащихся делают заранее подготовленные выступления из истории возникновения логарифмов. 1 ученик: Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n. Первым эту идею опубликовал в своей книге “Arithmetica integra” Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи. 2 ученик: В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием “Описание удивительной таблицы логарифмов”. В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке. Логарифмом числа x называют показатель степени y, в которую надо возвести некоторое фиксированное число a, чтобы получить исходное число x: ay=x. Записывают: y = loga x. Уже спустя 5 лет, в 1619 г., лондонский учитель математики Джон Спайделл переиздал таблицы Непера, преобразованные так, что они фактически стали таблицами натуральных логарифмов (хотя масштабирование до целых чисел Спайделл сохранил). Термин “натуральный логарифм” предложил итальянский математик Пьетро Менголи в середине XVI века. 3 ученик: И только в ХХ веке Владимир Модестович Брадис придумал способ, позволяющий до минимума сократить утомительные расчеты. Выбрать наиболее необходимые для инженерных расчетов функции, один раз посчитать их значения с приемлемой точностью в широком интервале аргументов. А результаты расчетов представить в виде таблиц. Кропотливых расчетов В.М. Брадису предстояло проделать много. Но они экономили массу времени всем последующим пользователям его таблиц. Эти таблицы стали советским бестселлером. С 1930 года их издавали едва ли не ежегодно в течение тридцати лет. III. Решение уравнений с помощью систем уравнений.
IV. Тест «Треугольник, круг, квадрат» Учитель: Сейчас каждый из вас выберет ту геометрическую фигуру, которая больше всего понравилась в данный момент. А теперь я даю характеристику каждой фигуре. А) Треугольник символизирует лидерство. Самой характерной особенностью человека, выбравшего этот символ, является способность концентрироваться на главной цели. Это сильная, энергичная, неудержимая личность. «Треугольник» ставит ясные цели и старается, по возможности, достичь их. Б) Квадрат. Основное качество личности, отдавшей предпочтение квадрату – трудолюбие, усердие, потребность доводить начатое дело до конца, упорство в достижении цели. «Квадрат» предпочитает раз и навсегда заведенный порядок: все должно находится на своем месте и происходить в свое время. В) Круг – самая доброжелательная фигура. Обладатель этого символа счастлив, когда все ладят друг с другом: круг ощущает чужую радость и боль, как свою собственную. Это очень чувствительная и эмоциональная натура. V. Итог урока. Сказка про число 666 (ученица рассказывает заранее подготовленную сказку). Прослушав сказку, учащиеся анализируют ее и делают выводы. Учитель выставляет оценки за урок и отмечает наиболее активных учащихся. VI Домашнее задание. П.9.2 №9.9г, 9.10г, 9.12б, 9.13б. Подготовка к ЕГЭ: повторить тему «Производная». Подготовить творческие сообщения «Применение логарифмов в химии, биологии, географии, физике, музыке, экономике, банковском деле и т.д.» VII Рефлексия. Что вас удивило, заинтересовало? Чем? Какой вид деятельности вам понравился больше всего? Какие мысли возникли у вас по теме урока? |
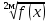=q(x) равносильно
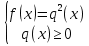Б).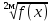
=
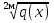равносильно 
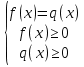для любого четного 2м (м€N). В).а
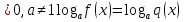равносильно 
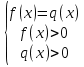Г). Уравнение f(x)+ψ(x)-ψ(x)=0 равносильно 