Глава 5. Элементы комбинаторики и теории вероятностей (13 часов)
Комбинаторное правило умножения. Перестановки, размеще�ния, сочетания. Относительная частота и вероятность случайного события.
Цель: ознакомить обучающихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний.
При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме обучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
Глава IX, X. Векторы и метод координат (18 часов)
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Основная цель — научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач. Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).
На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.
Глава XI. Соотношения между сторонами и углами треугольника (11 часов)
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах. Основная цель — развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.
Синус и косинус любого угла от 0° до 180° вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольника (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников.
Скалярное произведение векторов вводится как в физике (произведение длин векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач.
Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.
Глава XII. Длина окружности и площадь круга ( 12 часов)
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Основная цель — расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2ге-угольника, если дан правильный п-угольник.
Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь — к площади круга, ограниченного окружностью.
Глава XIII. Движения (8 часов)
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
Основная цель — познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений. Движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. При рассмотрении видов движений основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач. Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения.
Повторение(30 часов)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс математики 9 класса основной общеобразовательной школы.
Требования к уровню подготовки обучающихся в 9 классе
В ходе преподавания геометрии в 9 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали овла�девали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
В результате изучения курса математики 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к 0, у=кх+b, у=х2, у=х3, у = 0, у=кх+b, у=х2, у=х3, у =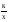 , у= , у=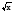 , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики; , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, комбинаторики,
статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
ГЕОМЕТРИЯ
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Список литературы:
Федеральный компонент государственных образовательных стандартов основного общего образования (приказ Минобрнауки от 05.03.2004г. № 1089).
Временные требования к минимуму содержания основного общего образования (утверждены приказом МО РФ от 19.05.98 № 1236).
Примерная программа по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г № 03-1263).
Примерная программа для общеобразовательных школ, гимназий, лицеев по математике 5-11 классы к учебному комплексу для 7-9 классов (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова Ю.Н., составители Г.М. Кузнецова, Н.Г. Миндюк– М: «Дрофа», 2004. – с. 86-91)
Оценка качества подготовки выпускников основной школы по математике/ Г.В.Дорофеев и др.– М.: Дрофа, 2000.
Алгебра-9:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2004 – 2007 год.
Изучение алгебры в 7—9 классах/ Ю. Н. Макарычев, Н. Г. Миндюк, С. Б. Суворова..— М.: Просвещение, 2005—2008.
Уроки алгебры в 9 классе: кн. для учите�ля / В. И. Жохов, Л. Б. Крайнева. — М.: Просвещение, 2005— 2008.
Алгебра: дидакт. материалы для 9 кл. / Л. И. Звавич, Л. В. Кузнецова, С. Б» Суворова. — М.: Просвеще�ние, 2007—2008.
Элементы статистики и теории вероятностей: Учеб пособие для обучающихся 7-9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк; под ред. С.А. Теляковского. –– М.: Просвещение,2001 -2007г.
Дополнительная литература:
Математика 5-11 классы: нетрадиционные формы организации контроля на уроках / авт.-сост. М.Е. Козина, О.М. Фадеева. - Волгоград, Учитель, 2007;
В.И.Жохов, Л.Б.Крайнева Уроки алгебры в 9 классе- М.: «Вербум - М», 2000;
Н.П.Кострикина Задачи повышенной трудности в курсе алгебры 7-9 классов - М : Просвещение», 1991;
Нестандартные уроки алгебры. 8 класс. Сост. Ким Н.А. – Волгоград: ИТД «Корифей», 2006;
Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл. / Л.В. Кузнецова, С.В. Суворова, Е.А. Бунимович и др. – М.: Просвещение, 2004;
А.Г. Мордкович, П.В.Семенов События. Вероятности. Статистическая обработка данных. 7-9 классы. – М.: «Мнемозина»,2003;
Конструирование современного урока математики: кн. для учителя / С.Г. Манвелов. – М.: Просвещение,2005.
Сборник заданий для подготовки к итоговой аттестации в 9 классе/ Ф.Ф.Лысенко и др.– ЛЕГИОН «Ростов-на-Дону», 2010.
Олимпиадные задания по математике. 9 класс / авт.-сост. С.П. Ковалёва. – Волгоград: Учитель,2007.
№
|
Название темы
|
Кол-во часов
|
Цели урока
|
Вид контроля. Измерители
|
Требования к уровню подготовки учащихся
|
Использование ЦОР
|
Дата проведения
|
По плану
|
фактически
|
Блок 1. Квадратичная функция (22ч)
Цель: расширить сведения о свойствах функций, ознакомить учащихся со свойствами
и графиком квадратичной функции
|
§ 1. Функции и их свойства (5ч)
|
1
|
Функция. Область определения и область значений функции
|
1
|
Рассмотреть понятие функции и способы её задания.
Вспомнить изученные ранее функции и их свойства.
|
С-1 (ДМ)
|
-уметь находить по значению аргумента значение функции и наоборот,-уметь находить область определения и область значения функции;-уметь строить более сложные графики функций
|
|
2.09
|
|
2
|
Функция. Область определения и область значений функции
|
1
|
С-2 (ДМ)
|
https://school-collection.edu.ru
Область определения и область значений функции
|
3.09
|
|
3
|
Свойства функций
|
1
|
Систематизация свойств функций и рассматривать их при исследовании любых функций и построение их графиков.
|
С-3 (ДМ)
|
-уметь определять нули функции, промежутки возрастания и убывания
|
https://school-collection.edu.ru
"Усвоение навыков и знаний по теме "Свойства функции"
|
3.09
|
|
4
|
Свойства функций
|
1
|
С-4 (ДМ)
|
-уметь определять нули функции, промежутки возрастания и убывания
|
5.09
|
|
5
|
Свойства функций
|
1
|
Тест №1 (УМК, П.И. Алтынов)
|
-уметь определять нули функции, промежутки возрастания и убывания
|
6.09
|
|
§ 2. Квадратный трехчлен (4 ч + 1ч. к/р)
|
6-7
|
Квадратный трёхчлен и его корни
|
2
|
Рассмотреть понятие квадратного трёхчлена, его корни, выделение квадрата двучлена.
|
С-5 (ДМ)
|
-уметь находить корни квадратного трехчлена
|
https://school-collection.edu.ru
Квадратный трехчлен
|
8.09
9.09
|
|
8
|
Разложение квадратного трёхчлена на множители
|
1
|
Обсудить разложение многочленов на линейные множители.
|
|
-уметь находить корни квадратного трехчлена;
-уметь раскладывать на множители квадратный трехчлен
|
|
10.09
|
|
9
|
Разложение квадратного трёхчлена на множители. Проверочная самостоятельная работа
|
1
|
С-6 (ДМ)
|
|
10.09
|
|
10
|
Контрольная работа №1 по теме: «Функции и их свойства. Квадратный трехчлен»
|
1
|
Проверка знаний учащихся с использованием разноуровневых вариантов.
|
|
Уметь применять изученную теорию при нахождении ООФ, ОЗФ, читать график, при разложении квадратного трехчлена на множители
|
|
12.09
|
|
§ 3. Квадратичная функция и ее график (8ч)
|
11-12
|
График функции у=ах2
|
2
|
Рассмотреть свойства и график простейшей квадратичной функции у=ах2
|
С-7 (ДМ)
|
-уметь строить график функции у=ах2;
-правильно читать график
|
https://school-collection.edu.ru
График квадратичной функции y=a(x - m) в квадрате
График квадратичной функции y=ax в квадрате + n
|
13.09
15.09
|
|
13-15
|
Графики функций у=ах2+n, у=а(x – m)2
|
3
|
Рассмотреть параллельный перенос графика функции.
|
С-8 (ДМ)
|
-уметь строить график функции, используя преобразования графиков
-знать алгоритм построения графика квадратичной функции;
|
16.09
17.09.
17.09
|
|
16
|
Построение графика квадратичной функции
|
1
|
Рассмотреть построения графика функции у=ах2+вх+с
|
|
-уметь находить координаты вершины параболы
-знать алгоритм построения графика квадратичной функции;
-уметь находить координаты вершины параболы
|
https://school-collection.edu.ru
Закрепление знаний и навыков по теме "Построение графика квадратичной функции"
|
19.09
|
|
17
|
Построение графика квадратичной функции
|
1
|
С-9 (ДМ)
|
20.09
|
|
18
|
Построение графика квадратичной функции
|
1
|
Тест № 2 (УМК)
|
22.09
|
|
§ 4. Степенная функция. Корень n – й степени (3ч + 1ч. к/р)
|
19
|
Функция у=хn
|
1
|
Рассмотреть свойства и график функции у=хn
|
С-10 (ДМ)
|
-знать свойства функции при n-четном и n-нечетном;
-уметь преобразовывать графики у=х2,у=х3 и с наиболее высокими степенями
|
https://school-collection.edu.ru
Нечетные функции
|
23.09
|
|
20
|
Корень n-й степени
|
1
|
Рассмотреть понятие корня натуральной степени n.
Рассмотреть определение и свойства степени с рациональным показателем.
|
С-11 (ДМ)
|
-знать таблицу степеней;
-уметь вычислять значения некоторых корней n-ой степени
|
https://school-collection.edu.ru
Определение корня n-й степени
|
24.09
|
|
21
|
Степень с рациональным показателем
|
1
|
|
-уметь применять свойства степени с рациональным показателем при решении задач.
|
https://school-collection.edu.ru
Закрепление знаний по теме "Определение степени с дробным показателем"
|
24.09
|
|
22
|
Контрольная работа № 2: «Квадратичная функция. Степенная функция»
|
1
|
Проверка знаний учащихся с использованием разноуровневых вариантов.
|
|
-уметь выполнять построение квадратичной функции, уметь применять таблицу степеней, вычислять значения некоторых корней n-й степени
|
|
26.09
|
|
Блок 2. Векторы. Метод координат. (18 ч)
Цель: научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач
|
§ 1. Понятие вектора (2ч)
|
23
|
Понятие вектора. Равенство векторов.
|
1
|
ввести понятие вектора, его длины, коллинеарных и равных векторов; научить учащихся изображать и обозначать векторы, откладывать от любой точки плоскости вектор, равный данному.
|
Проверка задач самостоятельное решение
|
Сформировать у учащихся представление о векторе,
-уметь изображать, обозначать вектор, нулевой вектор;
-знать виды векторов
|
|
27.09
|
|
24
|
Откладывание вектора от данной точки.
|
1
|
|
|
29.09
|
|
§ 2. Сложение и вычитание векторов. (3ч)
|
25
|
Сумма двух векторов
|
1
|
ввести понятие суммы двух векторов; рассмотреть законы сложения векторов; научить строить сумму двух данных векторов, используя правило треугольника и параллелограмма.
|
ФО
|
Знать законы сложения, определение суммы, правило треугольника, правило параллелограмма, уметь строить вектор, равный сумме двух векторов, используя правила треугольника, параллелограмма, формулировать законы сложения
|
|
30.09
|
|
26
|
Сумма нескольких векторов. Вычитание векторов
|
1
|
ввести понятие суммы трех и более векторов; научить строить сумму двух и нескольких векторов, используя правило многоугольника; учить решать задачи.
|
СР № 33
ДМ (8 кл)
|
Знать понятие суммы двух и более векторов, уметь строить сумму нескольких векторов, используя правило прямоугольника, Уметь строить вектор , равный разности двух векторов, двумя способами
|
https://school-collection.edu.ru
Задача 763 б,г
| | |
 Скачать 0.71 Mb.
Скачать 0.71 Mb. 0, у=кх+b, у=х2, у=х3, у =
0, у=кх+b, у=х2, у=х3, у =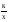 , у=
, у=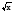 , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
, у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;