Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

Протокол № от «31» августа 2013 г. Руководитель / Казанцева О. М./ Утверждено Директор мобу



Скачать 497.9 Kb.
НазваниеПротокол № от «31» августа 2013 г. Руководитель / Казанцева О. М./ Утверждено Директор мобу
страница2/4
Дата05.04.2016
Размер497.9 Kb.
ТипПротокол
1   2   3   4

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления. Таким образом, в ходе освоения содержания курса обучающиеся получают возможность:


  • развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

  • овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

  • изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

  • развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

  • получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

  • развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

  • сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Курс математики 6 класса строится на индуктивной основе с привлечением дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.

В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают начальные представления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.

ОСНОВНОЕ СОДЕРЖАНИЕ

Тема: «Повторение курса математики 5-6 классов».

  • Числа и вычисления

Обязательный минимум содержания образовательной области математика

        Действия с натуральными числами.

        Действия с обыкновенными дробями.

        Действия с десятичными дробями.

Требования к математической подготовке Уровень обязательной подготовки обучающегося

        Уметь выполнять действия с обыкновенными дробями.

        Уметь выполнять действия с положительными и отрицательными числами.

        Уметь выполнять раскрытие скобок, приведение подобных слагаемых.

Уровень возможной подготовки обучающегося
        Уметь выполнять действия с обыкновенными дробями.

        Уметь выполнять действия с положительными и отрицательными числами.

        Уметь выполнять раскрытие скобок, приведение подобных слагаемых.

        Уметь решать текстовые задачи.

Тема: «Выражения. Тождества. Уравнения».

  • Числа и вычисления

  • Выражения и преобразования

  • Уравнение и неравенства

  • Статистические данные

Содержание обучения Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.

Основная цель - систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.

Первая тема курса 7 класса является связующим звеном между курсом математики 5 - 6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.

Нахождение значений числовых и буквенных выражений даёт возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычисления должно уделяться серьёзное внимание и в дальнейшем при изучении других тем курса алгебры.

В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, даётся понятие о двойных неравенствах.

При рассмотрении преобразований выражений формально - оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия "тождественно равные выражения", "тождество", "тождественное преобразование выражений", содержание которых будет постоянно раскрываться, и углубляться при изучении преобразований различных алгебраических выражений. Подчёркивается, что основу тождественных преобразований составляют свойства действий над числами.

Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ax=b при различных значениях a и b. Продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остаётся таким же, как в 6 классе.

Изучение темы завершается ознакомлением учащихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь использовать эти характеристики для анализа ряда данных в несложных ситуациях.

Обязательный минимум содержания образовательной области математика

  • Алгебраические выражения.

  • Буквенные выражения (выражения с переменными).

  • Числовое значение буквенного выражения.

  • Допустимые значения переменных, входящих в алгебраические выражения.

  • Подстановка выражений вместо переменных.

  • Преобразования выражений.

  • Уравнение с одной переменной.

  • Корень уравнения.

  • Решение текстовых задач алгебраическим способом.

  • Представление данных в виде таблиц, диаграмм, графиков.

  • Средние значения результатов измерений.

  • Понятие о статистическом выводе на основе выборки.

Требования к математической подготовке  Уровень обязательной подготовки обучающегося

  • Уметь осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления.

  • Уметь осуществлять подстановку одного выражения в другое.

  • Уметь выражать из формул одну переменную через остальные.

  • Знать правила раскрытия скобок.

  • Уметь решать уравнения с одним неизвестным, сводящиеся к линейным.

  • Уметь решать текстовые задачи алгебраическим методом.

  • Уметь извлекать информацию, представленную в таблицах, на диаграммах, графиках.

  • Уметь составлять таблицы.

  • Уметь строить диаграммы и графики.

  • Уметь вычислять средние значения результатов измерений.

Уровень возможной подготовки обучающегося

  • Знать как используются математические формулы для решения математических и практических задач.

  • Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами.

  • Знать как используются уравнения для решения математических и практических задач.

  • Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

  • Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц.

  • Понимать различные статистические утверждения.

Уровень обязательной подготовки выпускника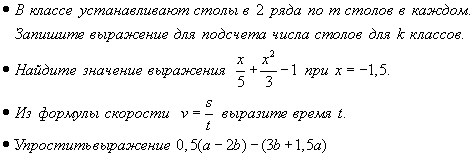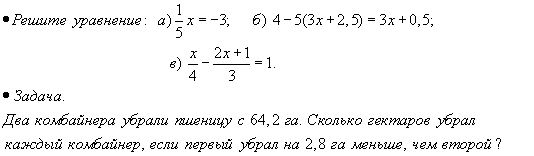

rp7am1

rp7am2

  • Выполните задание. В таблице показан расход электроэнергии некоторой семьей в течение года:

Месяц
1
2
3
4
5
6
7
8
9
10
11
12

Расход электроэнергии, квтч
85
80
74
62
54
68
58
54
58
64
74
86

Найдите средний ежемесячный расход электроэнергии этой семьей.

Уровень возможной подготовки выпускника

rp7am3

  • Задание: В организации вели ежедневный учет поступивших в течение месяца писем. В результате получили такой ряд данных: 39, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 25, 34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 32. Для полученного ряда данных найдите среднее арифметическое, размах и медиану. Каков практический смысл этих показателей? Тема: «Функции». Функции

Содержание обучения.

Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и её график. Линейная функция и её график.

Основная цель - ознакомить учащихся с важнейшими функциональными понятиями и с графиком прямой пропорциональности и линейной функции общего вида.

Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнить ту же задачу по графику и решить по графику обратную задачу.

Функциональные понятия получают свою конкретизацию при изучении линейной функции и её частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции y=kx, где k ≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида y=kx+b.

Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.

Обязательный минимум содержания образовательной области математика

  • Числовые функции. Понятие функции.

  • Способы задания функции.

  • График функции.

  • График линейной функции.

  • Чтение графиков функций.

Требования к математической подготовке

 Уровень обязательной подготовки обучающегося

  • Уметь находить значения линейной функции, заданной формулой, графиком по ее аргументу.

  • Уметь находить значение аргумента по значению линейной функции, заданной графиком.

  • Правильно употреблять функциональную терминологию.

Уровень возможной подготовки обучающегося

  • Понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

  • Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для интерпретации графиков реальных зависимостей между величинами.

Уровень обязательной подготовки выпускника

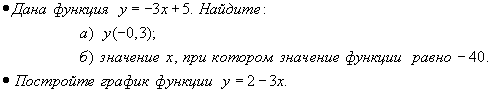rp7am4

Уровень возможной подготовки выпускника

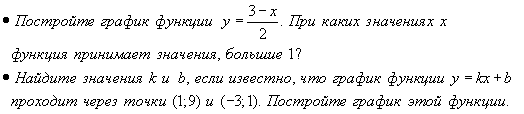rp7am5

Тема: «Степень с натуральным показателем».

  • Числа и вычисления

  • Выражения и преобразования

  • Функции

Содержание обучения. Степень с натуральным показателем и её свойства. Одночлен.

Функции y=x2, y=x3 и их графики.

Основная цель - выработать умение выполнять действия над степенями с натуральными показателями.

В данной теме даётся определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе даётся представление о нахождении значений степени с помощью калькулятора. Рассматриваются свойства степени с натуральным показателем. На примере доказательства свойств аm.аn=аm+n, аm:аn=аm-n , где m>n,( аm)n= аmn, (ав)n=аnвn

учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий.

Рассмотрение функций y=x2, y=x3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции y=x2: график проходит через начало координат, ось Оy является его осью симметрии, график расположен в верхней полуплоскости.

Умение строить графики функций y=x2, y=x3 используется для ознакомления учащихся с графическим способом решения уравнений.

Обязательный минимум содержания образовательной области математика

  • Степень с натуральным показателем.

  • Свойства степени с натуральным показателем.

  • Умножение одночленов.

Требования к математической подготовке  Уровень обязательной подготовки обучающегося

  • Уметь выполнять основные действия со степенями с натуральными показателями.

  • Уметь выполнять основные действия с одночленами.

Уровень возможной подготовки обучающегося

  • Уметь выполнять действия со степенями с натуральными показателями.

  • Уметь выполнять действия с одночленами.

Уровень обязательной подготовки выпускника

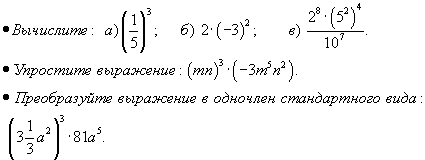rp7am6

Уровень возможной подготовки выпускника

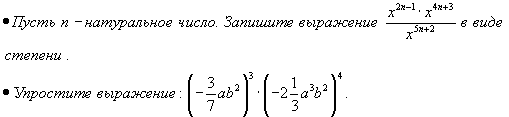rp7am7

Тема: «Многочлены».

  • Числа и вычисления

  • Выражения и преобразования

Содержание обучения. Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители. Основная цель - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально - оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.

Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.

Серьёзное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.

В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
Обязательный минимум содержания образовательной области математика

  • Сложение, вычитание, умножение многочленов.

  • Разложение многочлена на множители.

Требования к математической подготовке

 Уровень обязательной подготовки обучающегося

  • Уметь выполнять основные действия с многочленами.

  • Уметь выполнять разложение многочленов на множители.

Уровень возможной подготовки обучающегося

  • Уметь выполнять основные действия с многочленами.

  • Уметь выполнять разложение многочленов на множители.

Уровень обязательной подготовки выпускника

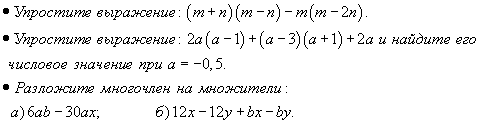rp7am8

Уровень возможной подготовки выпускника

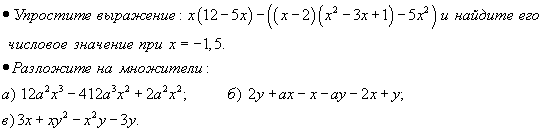rp7am9

Тема: «Формулы сокращенного умножения».

  • Числа и вычисления

  • Выражения и преобразования

Содержание обучения.

Формулы (а+ в)2=а2+2ав+в2, (а- в)2=а2-2ав+в2, (а+в)3=а3+3а2в +3ав2 +в3, (а+в)(а2-ав+в2)=а3+в3. Применение формул сокращённого умножения в преобразованиях выражения.

Основная цель - выработать умение применять формулы сокращённого умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.

В данной теме продолжается работа по формированию у учащихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (a - b) (a + b) = а2-в2 , а+в)2=а2+2ав+в2, (а-в)2=а2-2ав+в2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как "слева направо", так и "справа налево".

Наряду с указанными рассматриваются также формулы (а+в)3=а3+3а2в +3ав2 +в3, а3 +в3=(а+в)(а2-ав+в2). Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.

В заключительной части темы рассматривается применение различных приёмов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга

Обязательный минимум содержания образовательной области математика

  • Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности.

  • Формула разности квадратов, формула суммы кубов и разности кубов.

  • Разложение многочленов на множители.

Требования к математической подготовке

 Уровень обязательной подготовки обучающегося

  • Уметь выполнять разложение многочленов на множители.

  • Знать формулы сокращенного умножения.

  • Знать формулы разности квадратов, формулы суммы кубов и разности кубов.

Уровень возможной подготовки обучающегося

  • Уметь выполнять разложение многочленов на множители.

  • Знать формулы сокращенного умножения.

  • Знать формулы разности квадратов, формулы суммы кубов и разности кубов.

  • Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для нахождения нужной формулы в справочных материалах.


Уровень обязательной подготовки выпускника

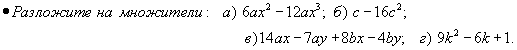rp7am10

Уровень возможной подготовки выпускника

7am

1   2   3   4