Стержень курса – математический язык и «мягкое» математическое моделирование. Из основных содержательно-методических линий школьного курса алгебры в качестве приоритетной выбрана функционально-графическая линия. Это выражается в том, что какой бы класс функций, уравнений, выражений ни изучался, построение материала всегда осуществляется по схеме: функция – уравнения – преобразования. Опираясь на опыт изучения функций, их свойств и графиков в 7-8 классах на наглядно-интуитивном и рабочем уровнях, в 9 классе осуществляется переход на уровень теоретического осмысления.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Целью изучения курса алгебры в 9 классе является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, информатика и другие), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществления функциональной подготовки школьников.
С учетом возрастных особенностей класса выстроена система учебных занятий, сформулированы характеристики основных видов деятельности ученика (на уровне учебных действий), продуманы возможные формы контроля: фронтальный опрос, индивидуальная работа, дифференцированная самостоятельная работа, математический диктант, тестовая работа, контрольная работа. Все виды контроля возможны с использованием компьютера.
В настоящей рабочей программе изменено соотношение часов на изучение тем в связи с тем, что несмотря на то, что в программе представлено тематическое планирование в двух варианта из расчета 3 часа и 4 часа в неделю, но разбивка часов в содержании программы представлена из расчета 3 ч в неделю (подробнее расписано в Содержании тем учебного курса).
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
Количество часов П/РП
Содержание программы направлено на освоение учащимися стандарта основного общего образования на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике.
Основное содержание по темам
|
Характеристика основных видов деятельности ученика
(на уровне учебных действий)
|
Повторение курса алгебры 7 – 8 классов (0/5ч)
|
Рациональные неравенства и их системы (16ч /19ч ).
|
Линейные и квадратные неравенства. Рациональные неравенства. Метод интервалов.
Множества и операции над ними.
Системы неравенств. Решение системы неравенств.
|
распознавать линейные и квадратные неравенства, решать линейные неравенства и квадратные неравенства с одной переменной, дробно-рациональные неравенства, неравенства, содержащие модуль;
понимать простейшие понятия теории множеств, приводить примеры конечных и бесконечных множеств, задавать множества, находить объединение и пересечение конкретных множеств;
описывать множество целых чисел, множество рациональных чисел, множество действительных чисел, соотношение между этими множествами;
решать системы линейных и квадратных неравенств, системы рациональных неравенств, двойные неравенства;
|
Системы уравнений (15 ч/23ч.).
|
Рациональное уравнение с двумя переменными. Решение уравнения р(х;у)=0. Равносильные уравнения с двумя переменными. Формула расстояния между двумя точками координатной плоскости. График уравнения (х – а) 2 + (у- в) 2 = r 2. Система уравнений с двумя переменными, решение системы уравнений с двумя переменными. Неравенства и системы неравенств с двумя переменными.
Методы решения систем уравнений (метод подстановки, метод алгебраического сложения, метод введения новых переменных, графический метод). Равносильные системы уравнений.
Системы уравнений как математические модели реальных ситуаций.
|
решать системы уравнений, простые нелинейные системы уравнений двух переменных различными методами;
строить графики уравнений с двумя переменными;
применять графический метод, метод подстановки, метод алгебраического сложения и метод введения новой переменной при решении практических задач;
решать неравенства и системы неравенств, используя графические представления;
использовать функционально – графическое представление для решения и исследования уравнений и систем
составлять математические модели реальных ситуаций и работать с составленной моделью;
|
Числовые функции ( 25 ч/32ч.)
|
Функция. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определения функции. Область значений функции.
Способы задания функции (аналитический, графический, табличный, словесный).
Свойства функций (монотонность (возрастание, ограниченность, выпуклость, наименьшее и наибольшее значения функции, непрерывность). Исследование функций: у = С, у = kx + m, y= kx 2, y = k/x, y = 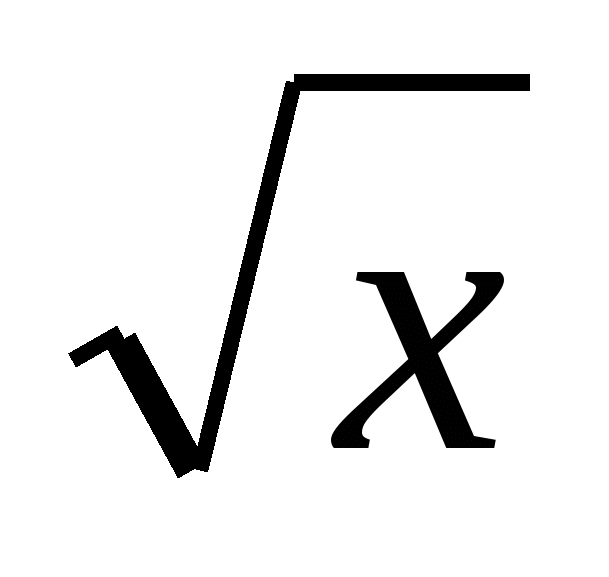 , y = |x|, y = ax 2 + bx + c. , y = |x|, y = ax 2 + bx + c.
Четные и нечетные. Алгоритм исследования функции на четность. Графики четной и нечетной функций.
Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показателем, ее свойства и график.
Функция у = 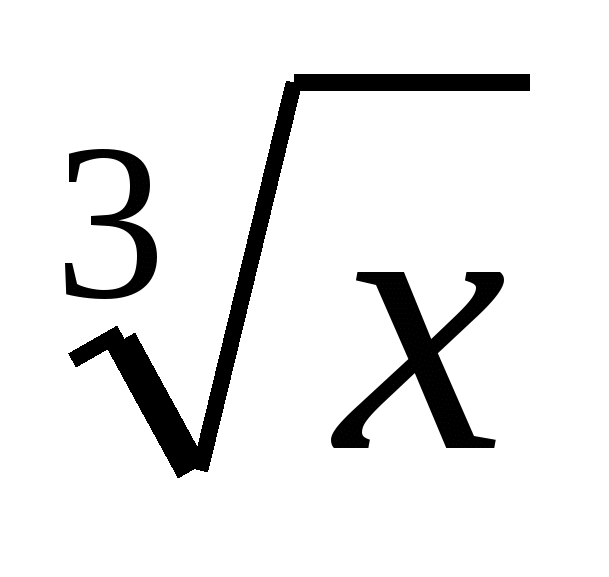 , ее свойства и график. , ее свойства и график.
|
Находить значения функции, заданной формулой, таблицей, графиком, по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
исследовать функцию на монотонность, определять наибольшее и наименьшее значение функции, ограниченность, выпуклость, четность, нечетность, область определения и множество значений; понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости графиков функций вида у = С, у = kx + m, y= kx 2, y = k/x, y = 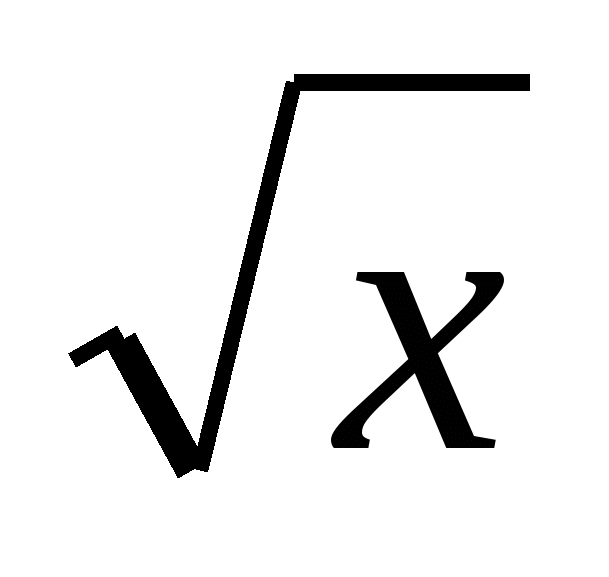 , y = |x|, y = ax 2 + bx + c в зависимости от значений коэффициентов, входящих в формулы; , y = |x|, y = ax 2 + bx + c в зависимости от значений коэффициентов, входящих в формулы;
описывать свойства изученных функций, строить их графики;
применять графические представления при решении уравнений, систем, неравенств
|
Прогрессии (16 ч/20 ч).
|
Числовая последовательность. Способы задания числовой последовательности (аналитический, словесный, рекуррентный). Свойства числовых последовательностей.
Арифметическая прогрессия, разность, возрастающая прогрессия, конечная прогрессия, формула n-го члена арифметической прогрессии, формула суммы членов конечной арифметической прогрессии, характеристическое свойство арифметической прогрессии.
Геометрическая прогрессия, знаменатель прогрессии, возрастающая прогрессия, конечная прогрессия, формула n-го члена геометрической прогрессии, формула суммы членов конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии. Прогрессии и банковские расчеты.
|
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
|
Элементы комбинаторики, статистики и теории вероятностей ( 12 ч/20ч.).
|
Комбинаторные задачи. Правило умножения Факториал. Перестановки.
Группировка информации. Общий ряд данных. Кратность варианты измерения. Табличное представление информации. Частота варианты. Графическое представление информации. Полигон распределения данных. Гистограмма. Числовые характеристики данных измерения (размах, мода, среднее значение).
Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Несовместные события. Вероятность суммы двух событий. Вероятность противоположного события. Статисическая устойчивость. Статистическая вероятность.
|
Проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность расссуждений, использовать примеры для иллюстрации и контр примеры для опровержения утверждений;
Извлекать информацию, представленную в таблицах, на диаграммах графиках, составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем системтатического перебора возможных вариантов, а также с использованием правила умножения;
находить размах, моду, среднее значение;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
приводить примеры достоверных и невозможных событий
находить вероятности случайных событий в простейших случаях
|
Обобщающее повторение ( 18 ч/16ч)
|
Административный контроль ( 0/3ч)
|
Структура курса
№ п/п
|
Тема (глава)
|
Кол-во часов по по программе
102
|
Количество часов по рабочей программе
136
|
1
|
Повторение
|
-
|
5
|
2
|
Неравенства и системы неравенств
|
16
|
19 +1акр
|
3
|
Системы уравнений
|
15
|
23
|
4
|
Числовые функции
|
25
|
32 + 2 акр
|
5
|
Прогрессии
|
16
|
20
|
6
|
Элементы комбинаторики, статистики и теории вероятностей
|
12
|
20
|
7
|
Итоговое повторение
|
18
|
16
|
КОНТРОЛЬ УРОВНЯ ОБУЧЕННОСТИ
ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ РАБОТ
№ п/п
|
Тема
|
Кол-во
часов
|
1
|
Контрольная работа №1. Неравенства и системы неравенств
|
1
|
2
|
Контрольная работа №2. Системы уравнений.
|
1
|
3
|
Контрольная работа №3. Свойства функций.
|
1
|
4
|
Контрольная работа №4. Числовые функции.
|
1
|
5
|
Контрольная работа №5. Прогрессии
|
1
|
6
|
Контрольная работа №6. Элементы комбинаторики, статистики и теории вероятностей
|
1
|
7
|
Итоговая контрольная работа (административный контроль)
|
2
| |
 Скачать 379.56 Kb.
Скачать 379.56 Kb.