Решение линейных неравенств; вывести понятия «системы рациональных неравенств», «решение рациональных неравенств»
 Скачать 46.7 Kb. Скачать 46.7 Kb.
|
| Конспект урока математики в 9 классе по теме: «Системы рациональных неравенств» Цели урока:
Ход урока: 1. Организационный момент 2. Работа по карточкам Карточка № 1. Решите неравенство: а) 5х+4<9х-12 б) х²+4х-21≥0 Карточка № 2. Решите неравенство: а) 8х+9≤ -4х+3 б) х²-2х-24≥0 Карточка № 3.
Карточка № 4.
2. Множество А состоит из делителей числа 30, а множество В – из делителей числа 45. Найдите пересечение и объединение данных множеств. (Карточки предлагаются 4 обучающимся, а в это время класс выполняет математический диктант) Математический диктант. (Слайд 2)
Для проверки приводится следующая таблица (слайд 3):
3. Подготовка к введению нового материала. Определение темы и целей урока. Учитель задаёт вопросы, обучающиеся отвечают на них.
Р 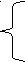 ешите систему уравнений (слайд 4): х-у=5 ешите систему уравнений (слайд 4): х-у=5х+у=7 (6;1) 4) Что такое рациональное неравенство? 5) Что значит решить неравенство? Рассмотрим два примера, решение которых, как мы увидим, приведет нас к новой математической модели. В этих примерах нам необходимо найти область определения выражений. (обучающиеся решают самостоятельно и проверяют по ключу) (слайд 5) Пример 1. √2х-4 П  ример 2. √8-х ример 2. √8-хА теперь рассмотрим выражение √2х-4 + √8-х. (слайд 6) - Как же найти его область определения? - Да она существует тогда, когда существует первый и второй корень одновременно. Что это вам напоминает? (ответы детей) - Вот мы и пришли к новой математической модели – система неравенств. - Какова же тема сегодняшнего нашего урока? (ответы обучающихся) - Да. Тема нашего урока: «Системы рациональных неравенств». (слайд 7) - Как вы думаете, какие вопросы могут возникнуть при изучении данной темы? - Из ваших ответов у нас получились цели урока. (слайд 8) - Что нам поможет в выполнении наших целей? 4. Изучение нового материала. - Вернемся к нашему выражению: √2х-4 + √8-х (слайд 9). Мы с вами сказали, что область определения данного выражения существует тогда, когда существует первый и второй корень одновременно. В этом случае говорят, что нужно решить систему неравенств 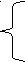 2х – 4 ≥ 0 2х – 4 ≥ 08 – х ≥ 0. - Что же такое система неравенств? - Прочитаем определение в учебнике (стр. 41) и сравним с тем, которое озвучили вы. - Мы решили каждое неравенство отдельно. А теперь, чтобы найти общее решение, поступим следующим образом: на числовой прямой Ох отметим сначала решение первого неравенства х ≥ 2, а затем на этой же прямой отметим решение и второго неравенства – х ≤ 8. Они пересекаются в отрезке [2; 8]. (Запись воспроизводится на доске) Следовательно решением этой системы будет отрезок [2; 8]. - Так что же является решением системы неравенств? И что значит решить систему неравенств? (ответы обучающихся) - Давайте рассмотрим простейшие, но очень важные опорные знания. Решим системы неравенств: 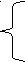 х > 7 Ответ: х > 10 х > 7 Ответ: х > 10х > 10 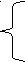 х > 7 Ответ: (7; 10] х > 7 Ответ: (7; 10]х ≤ 10 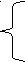 х ≤ 7 Ответ: х ≤ 7 х ≤ 7 Ответ: х ≤ 7 х ≤ 10 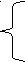 х ≥ 1 Ответ: [1; + ∞) х ≥ 1 Ответ: [1; + ∞)х² + 1≥ 0 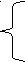 х ≥ 1 Ответ: нет решений или пустое множество. х ≥ 1 Ответ: нет решений или пустое множество. х < 1 В этом случае говорят, что система противоречива 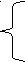 х ≤ 1 Ответ: х = 1 х ≤ 1 Ответ: х = 1х ≥ 1 - На основании этих примеров мы рассмотрели, что еще кроме отрезка может являться решением системы неравенств. Давайте вместе выведем определение понятию: решение системы неравенств (слайд 10). 5. Закрепление нового материала. Решение упражнений из задачника стр. 25 № 4.1 (устно), № 4.5 (а, б), № 4.6 (а, в), № 4.8 (в, г). 6. Проверочная работа. Самостоятельно решить № 4.8 (а, б). - На каких координатных прямых изображено множество решений системы первой системы? Второй системы? 7. Подведение итогов урока. Оценивание обучающихся. - Давайте вспомним цели, которые мы с вами ставили в начале урока. Всё ли мы выполнили? 8. Домашнее задание. Изучить материал § 4. Выполнить номера 4.7; 4.21 (а, б). по желанию: составить вопросы для проверки знания материалов § 4. (Слайд 11) |