«Применение производной для исследования функций на монотонность и экстремумы»
 Скачать 445 b. Скачать 445 b.
|

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
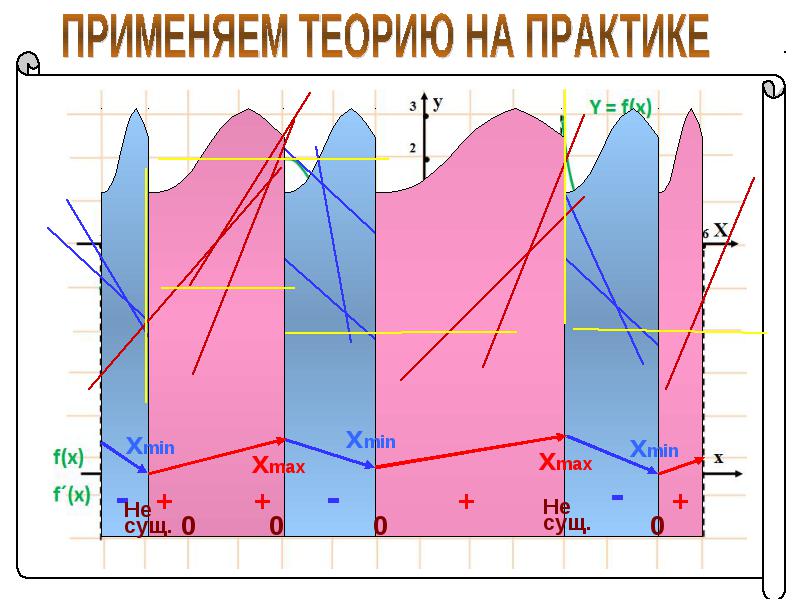
 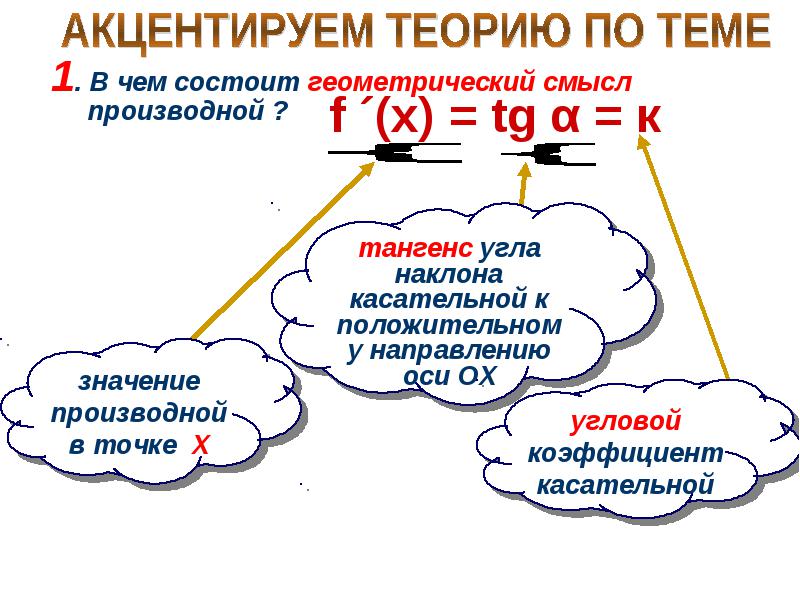 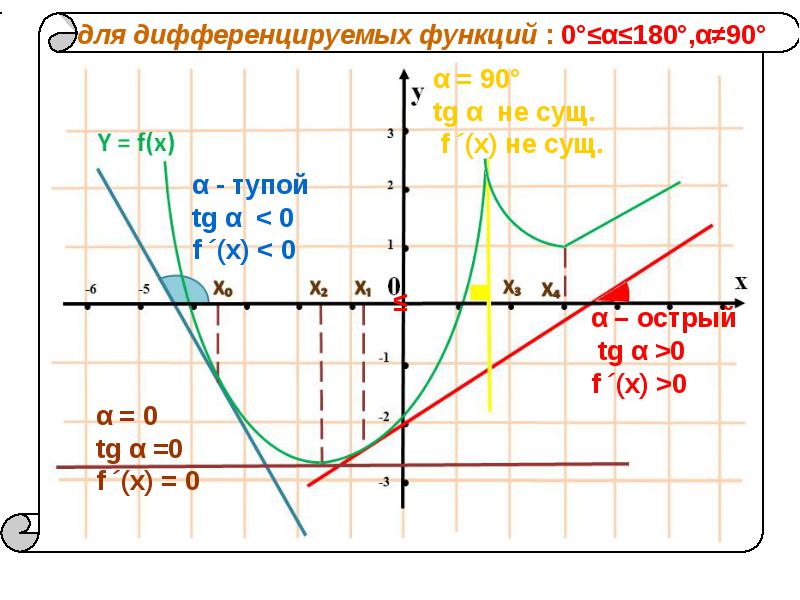 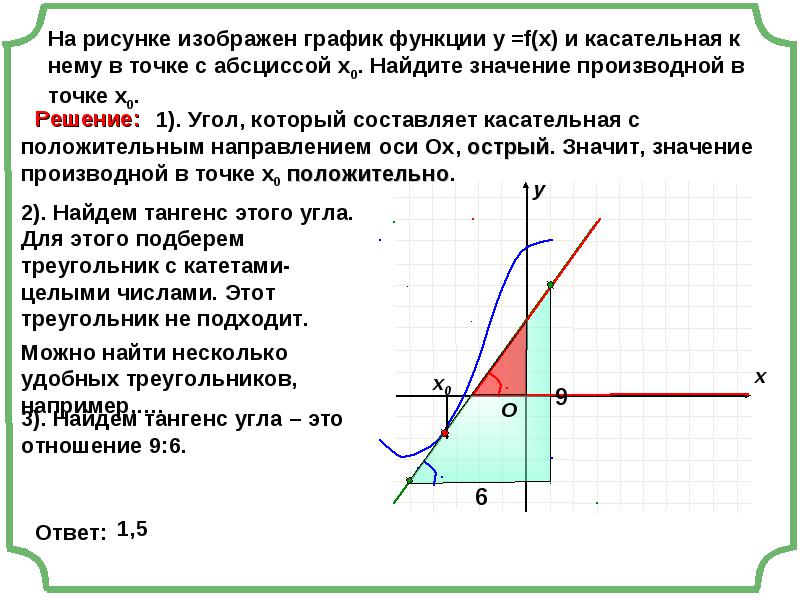  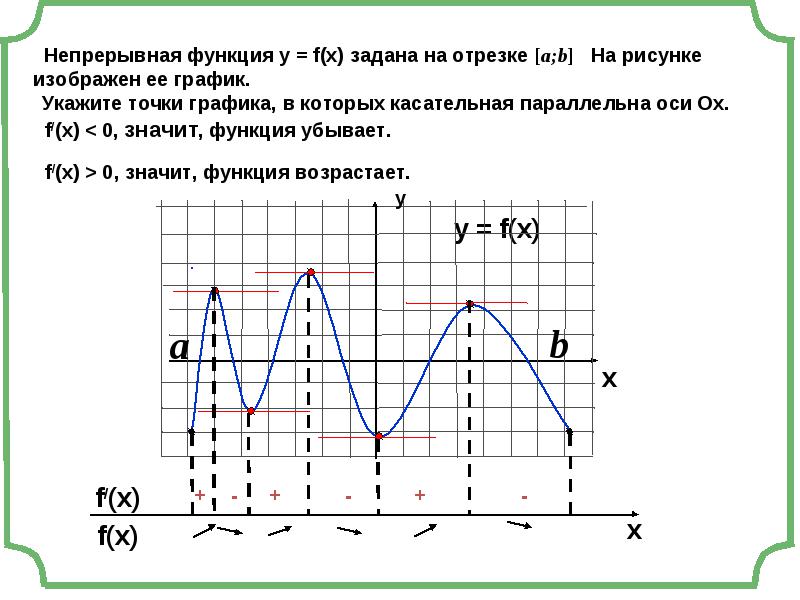 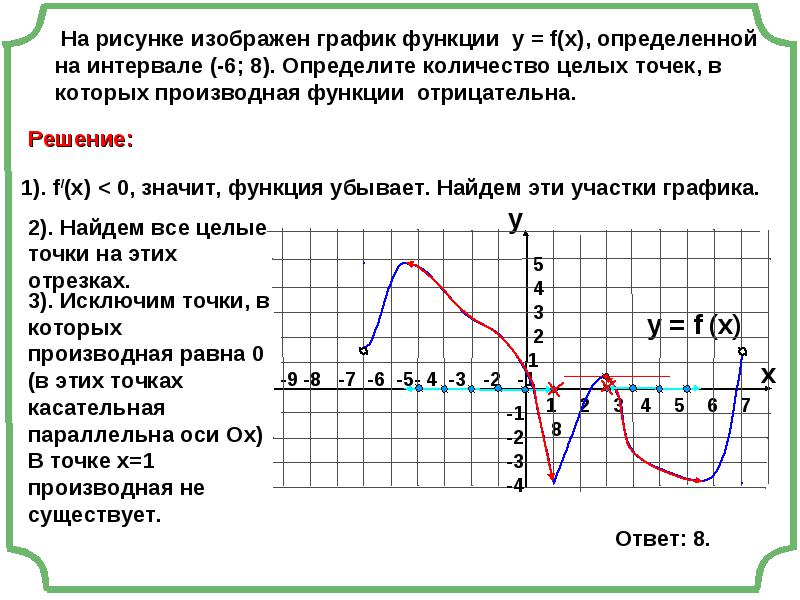 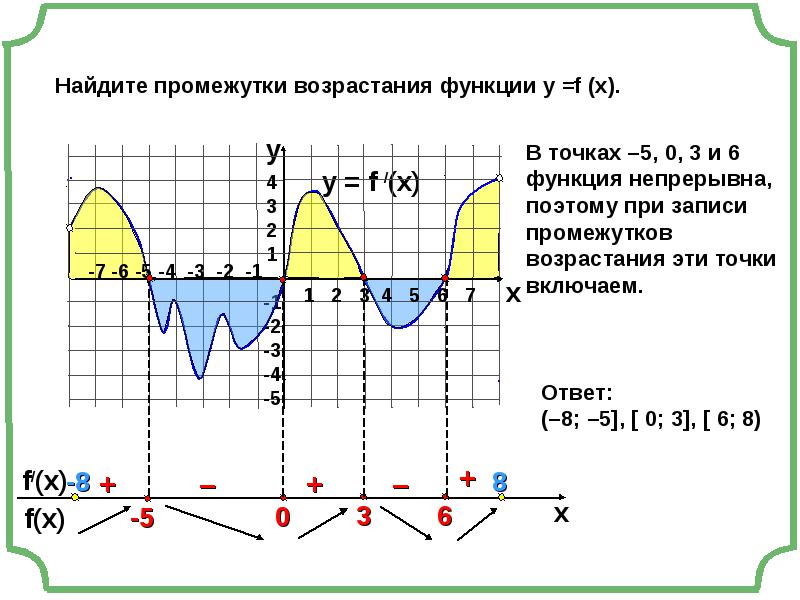 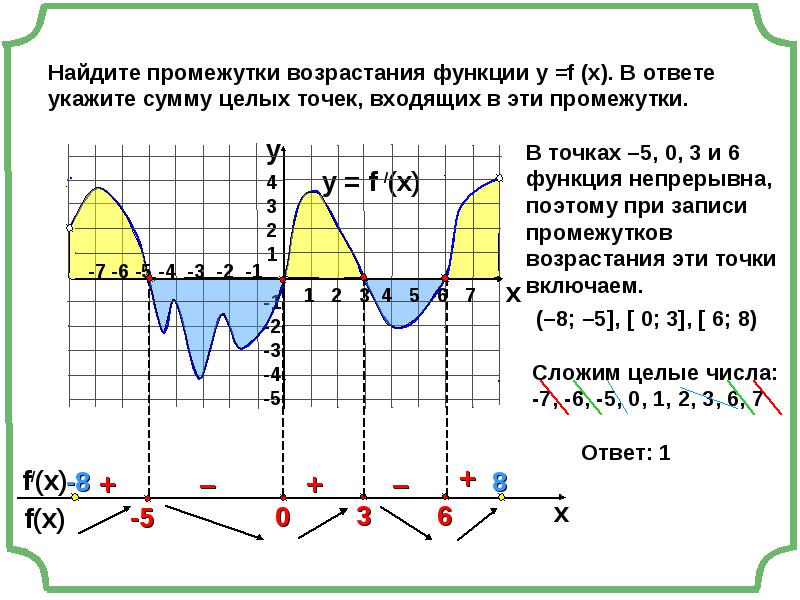  Связь производной со свойствами функции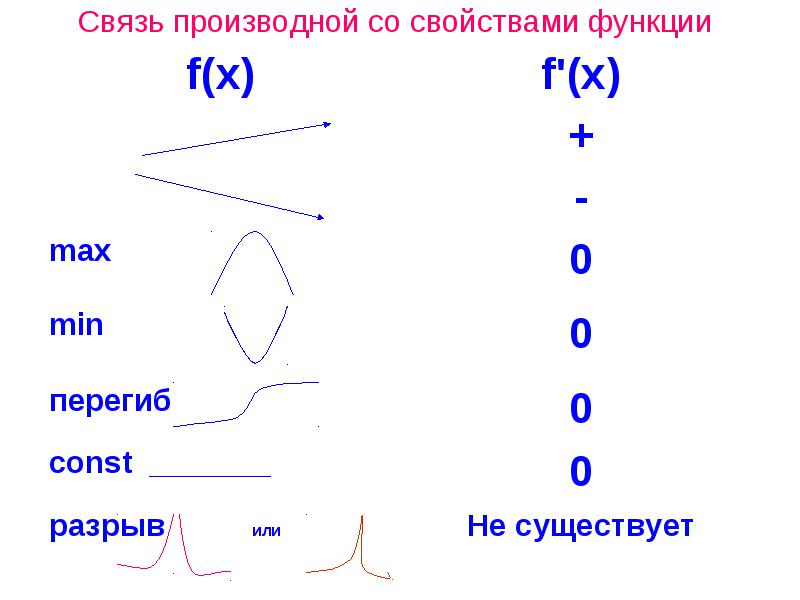 Правило нахождения интервалов монотонности
  |