Решение неравенств и систем неравенств с одной переменной. 8-й класс тема : Неравенства. Решение систем неравенств с одной переменной

Скачать 146.63 Kb. Название Решение неравенств и систем неравенств с одной переменной. 8-й класс тема : Неравенства. Решение систем неравенств с одной переменной Дата 05.04.2016 Размер 146.63 Kb. Тип Решение

Гаева О.Г. МБОУ СОШ № 29 Решение неравенств и систем неравенств с одной переменной. 8-й класс тема: Неравенства. Решение систем неравенств с одной переменной. Тип урока: урок обобщения, систематизации и контроля знаний. Цель урока: обобщение, систематизация и проверка знаний, умений и навыков в процессе решения неравенств и их систем. Задачи урока: 1. Учебные: Повторить и обобщить знания учащихся по теме «Неравенства с одной переменной и их системы» Продолжить формирование умений работать по алгоритму Выяснить область применение решения неравенств и систем неравенств закрепить умение применять свойства неравенств в процессе выполнения заданий; контроль уровня знаний, умений и навыков обучающихся по теме «Решение неравенств и систем неравенств с одной переменной». 2. Развивающие: развивать умение выделять главное; обобщать имеющиеся знания; развивать математическую речь Развивать навыки коллективной работы, взаимопомощи, самоконтроля. способствовать развитию интереса к предмету, организованности, ответственности. 3. Воспитательные: воспитывать мыслительную активность, самостоятельность; математическую зоркость, достигать сознательного усвоения материала обучающимися. Ход урока: I Организационная часть (Приветствие учителя, проверка готовности класса к работе.) - Сегодняшний урок я хотела бы начать с букета цветов, который я хочу вам подарить, а что при этом я хочу всем вам пожелать, вы узнаете в конце урока. На уроке мы заполняем листы контроля, зарабатывая оценки за урок. (Учитель совместно с учащимися объявляет цель урока. Урок начинается с высказывания : «Математика учит преодолевать трудности и исправлять собственные ошибки.» Р. Декарт) II Актуализация опорных знаний - Первый этап называется: “Без теории нет практики”. (Ученики работают в парах, спрашивая друг у друга теорию, связанную с темой урока.) Вопросы: Что значит решить неравенство? Что называется решением системы неравенств? Если скобки квадратные, то, какое неравенство, какая точка? Если точка закрашенная, то, какое неравенство, какие скобки? Если неравенство строгое, то какие будут точки на оси, какие скобки при написании ответа? Что значит решить систему неравенств? Что называется решением неравенства? Если точка пустая, то, какое неравенство, какие скобки? Если неравенство нестрогое, то какие будут точки на оси, какие скобки при написании ответа? Если скобки круглые, то, какое неравенство, какая точка? Критерии оценивания: 3 балла – знаю слабо; 4 балла – знаю хорошо, но иногда допускаю ошибки; 5 баллов – знаю очень хорошо, рассказываю без запинок. Отметьте результат в листе контроля. - Следующая задача сопоставить с помощью матричного теста: неравенство – числовой промежуток – координатную прямую. Работа по матричным тестам. (при необходимости в соответствующих клетках начертить координатную прямую и показать на ней решение неравенства) 1 вариант (а;в) а≤х≤в 0 х≥а 0 х<а 0 х>а 0 а≤х<в 0 а<х<в 0 х≤а 0 а<х≤в 0 2 вариант х≥а а≤х≤в х<а а≤х<в х>а а<х<в а<х≤в х≤а 0 0 0 0 0 0 (а;в) 0 0 Третий этап: тестирование с последующей проверкой и беседой по теории темы. Каждое задание теста предполагает ответ «Да» или «Нет». «Да» -1 «Нет» - 0. В результате выполнения теста получится какое-то число. Является ли число 12 решением неравенства 2х>10? 2) Является ли число -6 решением неравенства 4х>12? 3) Является ли неравенство 5х-15>4х+14 строгим? 4) Существует ли целое число принадлежащее промежутку [-2,8;-2,6]? 5) При любом ли значении переменной а верно неравенство а² +4 >о? 6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется? Назовите число, которое у вас получилось. Давайте проверим ответ. 101010. Отметьте результат в листе контроля. Мы вспомнили, как решаются неравенства, а теперь попробуем решить системы неравенств: 1) Решите систему неравенств: 2) Решите двойное неравенство: -10 < 8x - 2 < 14 ( по желанию выбирают любое и решают, те, кто решили первыми выходят к доске; кому нужна подсказка берут. В это время сильные и слабые учащиеся выполняют задание на индивидуальных карточках) При каких значениях переменной имеет смысл выражение а) б) в) Установить соответствие между неравенством и числовым промежутком Х ≥ 12 – 4 < Х ≤ 0 Х < – 0,3 2,5 ≤ Х < 10 3 < Х < 18 4 ≤ Х ≤ 12 1. (– ¥; – 0,3) 2. (3; 18) 3. [12; + ¥) 4. (– 4; 0] 5. [4; 12] 6. [2,5; 10) Отметьте результат в листе контроля. Этап: решаю сам. Формирование новых знаний: Где могут применятся системы неравенств? Посмотрите на задачу: Задача: Автомобиль по горной дороге за 7 часов проезжает больше 210 км, а по шоссе за 5 часов – не более 400 км. В каких пределах может изменяться его скорость? Анализ решения задачи. Краткая запись- составление таблицы. Ответ: скорость может изменяться в пределах (30; 80] Первичное закрепление: Задача. Одна сторона треугольника равна 5 метрам, а другая- 8 метрам. Какой может быть третья сторона, если периметр треугольника больше 17 метров ? 4< х < 13, значит, длина третьей стороны есть любое число из интервала 4< х < 13. Ответ: длина третьей стороны больше 4 метров, но меньше 13 метров. Отметьте результат в листе контроля: решил сам правильно-2; решил с подсказкой правильно-1; решил неверно-0. Контроль: Подготовка к ГИА. Тест: 1. Какой промежуток соответствует системе неравенств? 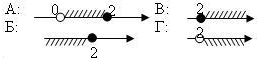2. Какая система неравенств соответствует данному числовому промежутку? 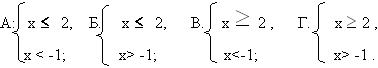3. Известно, что х 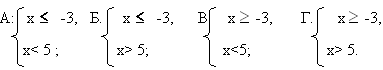[-3; 5). Какое из следующих неравенств соответствует этому? 4. На каком рисунке изображено множество решений х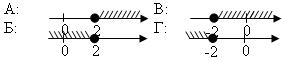[2;)? 5. Какое наименьшее целое число является решением данной системы? 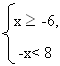А: -6; Б: - 8; В: 6; Г: 8. 6. Какова область определения функции у = А: (2;); Б: (-; 2]; В: [2;); Г: (-;2). Ответы: 1. Г; 2. Б; 3. В; 4. А; 5. А; 6. А; Критерии оценивания: по количеству правильных ответов. Отметьте результат в листе контроля Домашнее задание: в рабочих тетрадях стр. № -А теперь я хотела бы объяснить, что всем пожелала в начале урока. - Кто помнит, какие цветы были в моем букете? Итог: Сейчас вы тоже сможете составить букет, и подарить его кому- нибудь, но сначала ответьте на несколько вопросов, подписывать анкеты не обязательно. Что означают эти цветы вы узнаете на следующем уроке. Спасибо за внимание! Приложение: Лист контроля: Ф.И. Лист контроля: Ф.И. 1 Без теории нет практики 1 Без теории нет практики 2 Матричный тест 2 Матричный тест 3 Решаю сам 3 Решаю сам 4 Задача 4 Задача 5 Готовлюсь к ГИА 5 Готовлюсь к ГИА 6 Пожелание классу 6 Пожелание классу итого итого вариант I вариант II Что значит решить неравенство? Что значит решить систему неравенств? Что называется решением системы неравенств? Что называется решением неравенства? Если скобки квадратные, то, какое неравенство, какая точка? Если точка пустая, то, какое неравенство, какие скобки? Если точка закрашенная, то, какое неравенство, какие скобки? Если неравенство нестрогое, то какие будут точки на оси, какие скобки при написании ответа? Если неравенство строгое, то какие будут точки на оси, какие скобки при написании ответа? Если скобки круглые, то, какое неравенство, какая точка? 1 вариант Ф.И. (а;в) а≤х≤в х≥а х<а х>а а≤х<в а<х<в х≤а а<х≤в 2 вариант Ф.И. х≥а а≤х≤в х<а а≤х<в х>а а<х<в а<х≤в х≤а (а;в) При каких значениях переменной имеет смысл выражение При каких значениях переменной имеет смысл выражение а) а) б) б) в) в) Установить соответствие между неравенством и числовым промежутком (поставь цифру номера промежутка) Установить соответствие между неравенством и числовым промежутком (поставь цифру номера промежутка) 1. (– ¥; – 0,3) 2. (3; 18) 3. [12; + ¥) 4. (– 4; 0] 5. [4; 12] 6. [2,5; 10) Х ≥ 12 – 4 < Х ≤ 0 Х < – 0,3 2,5 ≤ Х < 10 3 < Х < 18 4 ≤ Х ≤ 12 1. (– ¥; – 0,3) 2. (3; 18) 3. [12; + ¥) 4. (– 4; 0] 5. [4; 12] 6. [2,5; 10) Х ≥ 12 – 4 < Х ≤ 0 Х < – 0,3 2,5 ≤ Х < 10 3 < Х < 18 4 ≤ Х ≤ 12 Алгоритм решения систем неравенств с одной переменной 1. Решить каждое неравенство системы. 2. Изобразить графически решения каждого неравенства на одной координатной прямой. 3. Найти пересечение решений неравенств на координатной прямой. 4. Записать ответ в виде числового промежутка. Алгоритм решения систем неравенств с одной переменной 1. Решить каждое неравенство системы. 2. Изобразить графически решения каждого неравенства на координатной прямой. 3. Найти пересечение решений неравенств на координатной прямой. 4. Записать ответ в виде числового промежутка.