№
п/п
|
Тема раздела, урока
|
Кол-во часов
|
Тип урока
|
Вид контроля,
измерители
|
Элементы содержания(дидактические единицы на основе общеобразовательного стандарта)
|
Планируемые результаты освоения уровня подготовки обучающихся
|
Дополнительные знания, умения (требования повышенного уровня)
|
Оборудование для демонстрации, лабораторных, практических работ
|
Примерное домашнее задание
|
|
Тригонометрические функции
|
11
|
Основная цель:
формирование представления об области определения и множества значений тригонометрических функций, нечетной и четной функции, периодической функции, наименьшем положительном периоде, об ограниченности функции;
формирование умений находить область определения и множество значений тригонометрических функций сложного аргумента, представленного в виде дроби и корня, нахождения наименьшего положительного периода функции или доказательства, что данная функция не является периодической;
овладение умением свободно строить графики функций повышенной сложности и описывать их свойства, решать уравнения, содержащие обратные тригонометрические функции;
овладение навыками преобразования выражений, содержащего обратные тригонометрические функции, решения графически уравнения и неравенства
|
1
|
Область определения и множество значений тригонометрических функций
|
1
|
Поисковый
|
Построение алгоритма решения задания
|
Область определения тригонометрических функций, множество значений тригонометрических функций, тригонометрические функции, ограниченность функции
|
Знают: как находить область определения и множество значений тригонометрических функций
Умеют: излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (Р)
|
Умеют: находить область определения и множество значений тригонометрических функций сложного аргумента, представленного в виде дроби и корня; осуществлять проверку выводов, положений, закономерностей, теорем. (П)
|
Слайд лекция «Тригонометрические функции»
|
Составление обобщающих информационных таблиц, повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §1 №1,2(четные)
|
2
|
1
|
исследовательский
|
Проблемные задания, ответы на вопросы
|
Умеют: находить множество значений тригонометрических функций вида kf(x)±m, где f(x)- любая тригонометрическая функция; приводить примеры, подбирать аргументы, формулировать выводы. (П)
|
Умеют: находить наибольшее и наименьшее значения функции y=kcosnx±lsinmx; доказывать ограниченность функции в области ее определения; самостоятельно искать и отбирать необходимую для решения учебных задач информацию. (ТВ)
|
Дифференцированные карточки по теме
|
Поиск нужной информации в различных источниках повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §1 № 3 (четные)
|
3
|
Четность, нечетность, периодичность тригонометрических функций
|
1
|
Объяснительно-иллюстративный
|
Решение упражнений, составление опорного конспекта, ответы на вопросы
|
Нечетная и четная функция, свойства четной и нечетной функций, периодическая функция, период функции, наименьший положительный период
|
Умеют: выяснять, является ли данная функция четной или нечетной; самостоятельно выбирать критерии для сравнения, оценки и классификации объектов. (Р)
|
Умеют: доказывать, что f(x)+f(-x)-четная функция, а f(x) –f(-x)- нечетная функция; излагать информацию, обосновывая свой собственный подход; формулировать полученные результаты. (П)
|
Слайд лекция «Тригонометрические функции»
|
Поиск нужной информации в различных источниках повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §2 №12,13(четные)
|
4
|
1
|
Учебный практикум
|
Фронтальный опрос, решение упражнений
|
Умеют: доказать, что данная функция является периодической с заданным периодом, находить наименьший положительный период функции или доказать, что данная функция не является периодической; воспроизводить теорию с заданной степени свернутости, участвовать в диалоге, подбирать аргументы для объяснения ошибки. (П)
|
Умеют: определять период сложно заданных тригонометрических функций; доказывать, что функция периодическая и находить ее наименьший положительный период; аргументированно рассуждать, обобщать; участвовать в диалоге, понимать точку зрения собеседника, приводить примеры; оформлять решение, выполнять задания по заданному образцу. (ТВ)
|
Тестовые материалы
|
Поиск нужной информации в различных источниках повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §2 № 14,15(четные)
|
5
|
Свойства функции y=cosx и ее график
|
1
|
Проблемный
|
Проблемные задачи, фронтальный опрос, упражнения
|
Тригонометрическая функция y=cosx, график функций, свойства функций
|
Знают: Тригонометрические функции y=cosx, их свойства.
Умеют: объяснять изученные положения на самостоятельно подобранных конкретных примерах. (Р)
|
Умеют: совершать преобразования графиков функций y=cosx; отбирать и структурировать материал; участвовать в диалоге. (П)
|
Слайд лекция «Тригонометрические функции»
|
Анализ условий задач, составление математической мод повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §3 № 29,31,33 (четные)
|
6
|
1
|
Учебный практикум
|
Построение алгоритма действия, решение упражнений, ответы на вопросы
|
Умеют: построить и исследовать функции на четность и нечетность, находить область определения; находить все корни уравнения, принадлежащие промежутку; извлекать необходимую информацию из учебно-научных текстов, излагать информацию, разъясняя значение и смысл теории. (П)
|
Умеют: свободно строить графики повышенной сложности и описывать их свойства; решать графически уравнения и неравенства; находить все принадлежащие промежутку решения неравенства; добывать информацию по заданной теме в источниках различного типа. (ТВ)
|
Дифференцированные карточки по теме
|
Поиск нужной информации в различных источниках, повтор. Арифметические задачи В1, графики и диаграммы (2-3 задачи) §3 № 35,37(четные)
|
7
|
Свойства функции y=sinx и ее график
|
1
|
Объяснительно – иллюстративный, учебный практикум
|
Составление опорного конспекта, ответы на вопросы
|
Тригонометрические функции: y=sinx, график функции, свойства функции
|
Знают: тригонометрические функции y=sinx, их свойства.
Умеют: объяснять изученные положения на самостоятельно подобранных конкретных примерах. (Р)
|
Умеют: совершать преобразования графиков функций y=sinx; решать графически уравнения и неравенства; находить все принадлежащие промежутку решения неравенства; извлекать необходимую информацию из учебных текстов. (П)
|
Слайд лекция «Тригонометрические функции»
Опорные конспекты учащихся
|
Поиск нужной информации в различных источниках повтор. Простейшие уравнения В7 (2-3 задачи) §4 № 52,54,59 (четные)
|
8
|
Свойства функции y=tgx и ее график
|
1
|
Комбинированный
|
Составление опорного конспекта, ответы на вопросы
|
Тригонометрические функции: y=tgx, y=ctgx график функций, свойства функций
|
Знают: тригонометрические функции y=tgx, y=ctgx, их свойства.
Умеют: строить графики; использовать для решения познавательных задач справочную литературу. (Р)
|
Умеют: совершать преобразования графиков функций y=tgx, y=ctgx, зная их свойства; решать графически уравнения и неравенства; находить все принадлежащие промежутку решения неравенства; извлекать необходимую информацию из учебных текстов. (П)
|
Слайд лекция «Тригонометрические функции»
Опорные конспекты учащихся
|
Поиск нужной информации в различных источниках повтор. Простейшие уравнения В7 (2-3 задачи) §5 № 76,80,81 (четные)
|
9
|
Обратные тригонометрические функции
|
1
|
Объяснительно-иллюстративный
|
Индивидуальное решение контрольных заданий
|
Функции
y=arcsin x,
y=arcos x,
y=arctgx,
y=arcctgx, их свойства, графики; соотношения, содержащие арксинус, арккосинус, арктангенс, арккотангенс
|
Знают: обратные тригонометрические функции, их свойства, графики.
Умеют: строить графики обратных тригонометрических функций, описывать их свойства; решать уравнения содержащие обратные тригонометрические функции; приводить примеры, подбирать аргументы, формулировать выводы. (Р)
|
Умеют: преобразовывать выражения содержащие обратные тригонометрические функции; свободно доказывать тождества, содержащие обратные тригонометрические функции; преобразовывать выражения и решать уравнения, содержащие обратные тригонометрические функции сложного аргумента. (П)
|
Слайд лекция «Тригонометрические функции»
|
Создание базы тестовых задания по теме
§6 № 98,99,100(четные) повтор. Простейшие уравнения В7 (2-3 задачи)
|
10
|
Обобщающий урок по теме «Тригонометрические функции»
|
1
|
Урок обобщения и систематизации знаний
|
Проблемные задания , работа с демонстрационным материалом
|
|
Совершенствуются умения в исследовании элементарных тригонометрических функций методами элементарной математики. При изучении данной темы у учащихся формируются ключевые компетенции: способность самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем, умение мотивированно отказываться от образца, искать оригинальные решения
|
Раздаточные дифференцированные задания
|
Разработка кластера своего проекта обобщения материала, стр. 41 Проверь себя!
|
11
|
Контрольная работа № 1 по теме «Тригонометрические функции»
|
1
|
Урок контроля, обобщения и коррекции знаний
|
Индивидуальное решение контрольных заданий
|
|
Умеют: оформлять решения, выполнять задания по заданному алгоритму; работать с чертежными инструментами; предвидеть возможные последствия своих действий. (П)
|
Умеют: классифицировать и проводить сравнительный анализ, рассуждать и обобщать, аргументированно отвечать на вопросы; контролировать и оценивать свою деятельность; находить и устранять причины возникших трудностей. (ТВ)
|
Дифференцированные контрольно-измерительные материалы
|
Создание варианта контрольной работы по теме
|
|
Производная и ее геометрический смысл
|
18
|
Основная цель:
формирование понятий мгновенной скорости, касательной к плоскости кривой, касательной к графику функции, производной функции, физическом смысле производной, геометрическом смысле производной, скорости изменения функции, пределе функции в точке, дифференцировании, производных элементарных функций;
формирование умения использовать алгоритм нахождения производной элементарных функций простого и сложного аргумента;
овладение умением находить производную любой комбинации элементарных функций, вывести формулы нахождения производной сложной функции ;
овладение навыками составлять уравнения касательной к графику функции при дополнительных условиях касательной к графику, находить угловой коэффициент, точку касания.
|
12
|
Предел последовательности
|
1
|
Проблемный
|
Проблемные задачи. Построение алгоритма действия
|
Числовая последовательность, предел числовой последовательности, элемент последовательности, множество значений последовательности, рекуррентная формула, последовательность Фибоначчи; стационарная последовательность, последовательность сходится и расходится, предел монотонной последовательности, вычисление предела последовательности, число e.
|
Знают: свойства сходящихся последовательностей.
Умеют: изображать на числовой прямой несколько членов последовательности 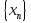 и выяснять, к какому числу они принадлежат; находить пределы последовательностей, сумму бесконечной геометрической прогрессии. (Р)
|
Умеют: доказывать теоремы о пределе возрастающей и убывающей последовательности; находить предел числовой последовательности, используя свойства сходящихся последовательностей, элементами которой являются члены арифметической последовательности. (П)
|
Слайд лекция «Теория пределов»
|
Поиск нужной информации в различных источниках
§1 № 1,2(четные) повтор. Простейшие уравнения В7 (2-3 задачи)
|
13
|
Непрерывность функции
|
1
|
Комбинированный
|
Взаимная проверка в парах. Работа с текстом
|
Точки непрерывности, точки разрыва, непрерывность функции в точке, непрерывность слева, справа, приращение аргумента, приращение функции, непрерывность функции на интервале, свойства функций, непрерывных на отрезке
|
Умеют: строить графики функций и выяснять, является ли эта функция непрерывной не всей числовой прямой, на каких промежутках функция непрерывна
4 извлекать необходимую информацию из учебно-научных текстов. (Р)
|
Умеют: доказывать теорему о промежуточных значениях функции и об обратной функции; приводить примеры, подбирать аргументы, формулировать выводы, собирать материал для сообщения по заданной теме. (П
|
Слайд лекция «Теория пределов»
|
Составление обобщающих информационных таблиц
§3 № 14-17 (четные) повтор. Простейшие уравнения В7 (2-3 задачи)
|
14
|
Определение производной
|
1
|
Комбинированный
|
Взаимопроверка в парах. Работа с текстом
|
Мгновенная скорость, разностное отношение, производная функции, скорость изменения функции, предел функции в точке, дифференцирование
|
Умеют: извлекать необходимую информацию из учебных текстов.
Имеют представление о понятии производной функции, скорости изменения функции. (Р)
|
Умеют: использовать определение производной для нахождения производной простейших функций; приводить примеры, подбирать аргументы, формулировать выводы; собирать материал для сообщения по заданной теме. (П)
|
Слайд лекция «Производная»
|
Составление обобщающих информационных таблиц, повтор. Простейшие уравнения В7 (2-3 задачи)
§4 № 23-25(четные)
|
15
|
1
|
Применение и совершенствование знаний
|
Практикум, фронтальный опрос, работа с раздаточным материалом
|
Умеют: находить производные от функции вида kx+d, 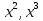 ; объяснять изученные положения на самостоятельно подобранных конкретных примерах; развернуто обосновывать суждения. (П)
|
Умеют: находить мгновенную скорость движения точки в каждый момент времени, если задан закон движения; объяснять изученные положения на самостоятельно подобранных конкретных примерах. (ТВ)
|
Раздаточные дифференцированные задания
|
Использование справочной литературы, а также ресурсов Интернет,
повтор. Простейшие уравнения В7 (2-3 задачи) §4№ 26,27(четные)
|
16
|
Производная степенной функции
|
1
|
Комбинированный
|
Составление опорного конспекта, ответы на вопросы
|
Производная степени, производная корня, производная числа, производная степени сложного аргумента, формула нахождения производной степенной функции
|
Знают: понятия производной степени. Корня.
Умеют: объяснять изученные положения на самостоятельно подобранных конкретных примерах. (Р)
|
Умеют: использовать алгоритм нахождения производной степени и корня; решать уравнения вида 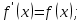 передавать информацию сжато, полно, выборочно. (П)
|
Слайд лекция «Производная»
|
Составление опорного конспекта, ответы на вопросы, повтор. В11 (2-3 задачи) §6 № 46-48(четные)
|
17
|
1
|
Учебный практикум
|
Решение упражнений, учебный практикум
|
Умеют: вычислять производную степенной функции и корня; участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение; находить и использовать информацию. (П)
|
Умеют: по данному графику квадратичной функции писать формулы, задающие саму производную; проводить самооценку собственных действий. (ТВ)
|
Опорные конспекты учащихся
|
Поиск нужной информации в различных источниках повтор. В11 (2-3 задачи) §6 № 49,50(четные)
|
Скачать 0.69 Mb.