Урок алгебры в 9-м классе по теме: "Решение неравенств второй степени с одной переменной"

Название	Урок алгебры в 9-м классе по теме: "Решение неравенств второй степени с одной переменной"
Дата	05.04.2016
Размер	76.81 Kb.
Тип	Урок

Урок алгебры в 9-м классе по теме:

"Решение неравенств второй степени с одной переменной"

Учитель математики МКОУ Красноэховская СОШ

Климова Светлана Николаевна

Цель:

Развивающая:

Развивать умение выделять главное, сравнивать, обобщать изучаемые факты;
Развивать логическое мышление и математическую речь;
Развивать внимание.
формирование умений решать неравенства второй степени с одной переменной на основе свойств квадратичной функции;
развитие навыков самоконтроля;
воспитание волевых качеств личности.

Образовательная:

Знать определение неравенств второй степени с одной переменной.
Уметь решать неравенства второй степени с одной переменной графическим способом.

Воспитательная:

Воспитание коммуникативных навыков: умение слышать и слушать.

Средства информационных технологий:

мультимедийный проектор;

интерактивная доска

компьютер

Сегодня будем работать под девизами:

Лучший способ изучить что-либо - это открыть самому. (Д. Пойа)

Правильному применению методов можно научиться только применяя их на разнообразных примерах. (Г. Цейтен)

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. (Д. Пойа)

В конце урока узнаем, как повлияли девизы на нашу работу

Этапы урока	Деятельность учителя	Деятельность учащихся	Время
Сообщение темы, целей урока. Проблемные вопросы.	Исходя из темы урока, очевидно, сегодня предстоит знакомство с решением неравенств второй степени, использующих свойства квадратичной функции. Как связаны эти понятия? Как бы вы предложили исследовать связь между ними? На какие вопросы стали отвечать в первую очередь?	Учащиеся дают ответы, выдвигают гипотезы	2 мин
Повторение ранее изученного материала (на слайде)	Задает вопросы: 1.Выражение какого вида называется квадратным трёхчленом? 2. Что надо сделать, чтобы найти корни квадратного трёхчлена? 3. Как называется функция вида у = ах² +вх + с ? 4. Что является графиком квадратичной функции? 5. От чего зависит направление ветвей?	Отвечают на поставленные учителем вопросы: 1.ax²+bx+c 2. ax²+bx+c=0 3. Квадратичной 4. Парабола 5. От коэффициента а, если а > 0, то ветви вверх, если a < 0, то ветви вниз	3 мин
Формирование новых понятий (на слайде)	Задает наводящие вопросы: 1.Какой вид имеет неравенство второй степени с одной переменной? 2.Что такое Х ? 3.Что такое a,b,c? 4.Какие ограничения для коэффициента а?	Дают определение неравенству второй степени с одной переменной Определение: 1.Неравенства вида ах² + вх + с > 0 и ах² + вх + с < 0 2.где х - переменная, 3.а, в, с –некоторые числа, 4.причем а≠0, называются неравенствами второй степени с одной переменной Записывают определение в тетрадь	4 мин
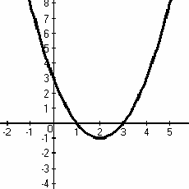
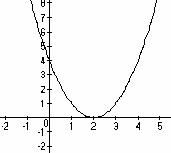
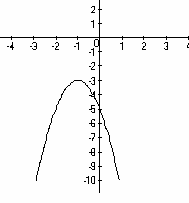
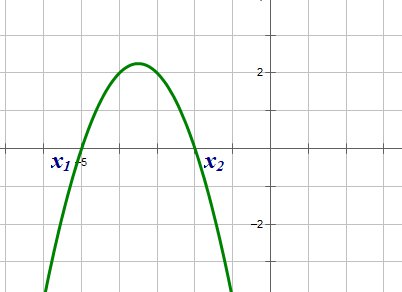
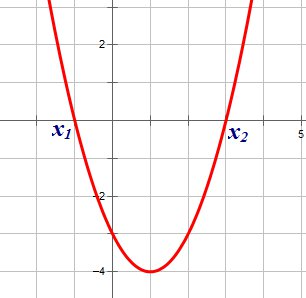
Актуализация опорных знаний и умений учащихся	Устная работа По схеме определите знаки коэффициентов a, b, c и D. Назовите промежутки, при которых y > 0, y < 0, то есть промежутки знакопостоянства функции.	Свои ответы ученики записывают в тетрадях, затем самостоятельно проверяют с записью на доске. Ответы: 1.a > 0, b < 0, c > 0, D > 0 2.a > 0, b < 0, c > 0, D = 0 3.a < 0, b < 0, c < 0, D < 0 Учащиеся записывают ответы в тетрадях и проверяют с верными: 4.a < 0, b < 0, c < 0, D > 0 5. a > 0, b > 0, c < 0, D > 0 1. y > 0 на (-∞; 1)U (3;+∞); y < 0 на (1;3). 2. y > 0 на (-∞; 2) U (2;+∞). 3. y < 0 на (-∞;+∞). 4. y > 0 на (-5;-2). y < 0 на (-∞; -5)U (-2;+∞); 5.y > 0 на (-∞;- 1)U (3;+∞); y < 0 на (-1;3).	6 мин
Формирование новых умений	Вернемся к поставленным вопросам. Какие появились идеи? Какой способ решения неравенств будем использовать? Кто может сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.	Предлагают варианты своих действий	3 мин
Выполнение практических заданий	Решить несколько неравенств второй степени с одной переменной: 1.х²-7х+10>0 2.- х² - 3х + 4 ≥ 0 3. 4. х² – 3х + 4 > 0 После разбора этих примеров попробуем вместе сделать некоторые выводы и зафиксируем их в тетрадях. Работа по интерактивной доске, на которой записано задание: Вам предстоит решить неравенство. Какая информация о квадратичной функции может оказаться при этом полезной, а какая лишней: - знак коэффициента; - знак D квадратного трёхчлена; - направление ветвей параболы; -пересечение параболы с осями координат; - координаты вершины параболы; - примерное расположение параболы? Обязательно ли для решения строить график соответствующей квадратичной функции? Если да, то с какой точностью выполнять построение. Задание: (записано на оборотной стороне интерактивной доски) Проанализируйте решение	Оформление решений неравенств в тетрадях Работа по слайдам презентационной программы Применяется эффект «шторки», ненужное в ходе обсуждения зачеркивается. Проблемный диалог с учащимися Учащиеся делают выводы. Самостоятельная проверка выводов Учащиеся делают вывод. После обсуждения, появляется алгоритм, который распечатывается через принтер интерактивной доски на каждую парту.	12 мин
Закрепление нового материала	Делает выводы вместе с учащимися и дает алгоритм решения неравенств второй степени с одной переменной: Чтобы решить неравенства вида ах² + вх + с > 0 и ax² + вx + c < 0 надо: 1.Найти дискриминант квадратного трехчлена и его корни 2.Отметить корни на оси х 3.Через отмеченные точки провести параболу, «ветви» которой направлены - вверх, если а > 0, - вниз, если a < 0 4. Если корней нет, то параболу изобразить в верхней полуплоскости при а > 0 в нижней полуплоскости при а < 0 5.Для неравенства ах² + вх +с>0 сделать штриховку над осью х 6.Для неравенства ах² + вх +с<0 сделать штриховку под осью х 7. Заштрихованные промежутки записать в ответ	Учащиеся делают вывод. После обсуждения, появляется алгоритм, который распечатывается через принтер интерактивной доски на каждую парту.	5 мин
Физминутка	Зарядка для глаз от профессора Владимира Жданова 1.Подняли глазки вверх, вниз, вверх, вниз, вверх, вниз, поморгали-поморгали-поморгали 2. Скосили глазки вправо, влево, вправо, влево, вправо, влево, Поморгали 3. Диагональ. Смотрим вправо вверх-влево вниз, влево вверх-вправо вниз, вправо вверх-влево вниз, влево вверх-вправо вниз. Поморгали 4. Прямоугольник. Подняли глазки наверх, нарисовали верхнюю сторону прямоугольника, правую боковую, нижнюю и левую боковую. И опять так же. В обратную сторону. Против часовой стрелки. Верхняя, левая, нижняя и правая. 5. Циферблат. Представьте перед собой огромный циферблат. Осматриваем его по часовой стрелке. Подняли глаза на 12 часов, 3 часа, 6, 9, 12 и в обратную сторону. 6. Змейка. Начинаем рисовать с хвоста. Глазки влево вниз, вверх, вниз, вверх, вниз, вверх и голова и назад.
Закрепление изученного материала.	Используя алгоритм, решите неравенства: X²-2x+1>0 ; X²+4x-4≥0 На интерактивной доске появляется общая таблица решения всех видов неравенств	Учащиеся выполняют работу самостоятельно. Самопроверка Ее переносят к себе в тетрадь	10 мин
Итоги урока. Рефлексия.	Обсуждается алгоритм решения неравенств второй степени. (по одному ученику) Сегодня я узнал … Было трудно Было интересно … Я понял, что… Теперь я могу … Я попробую … Я научился … Меня заинтересовало … Меня удивило …	Учащиеся записывают домашнее задание. Записать исходя из таблицы все случаи возможных решений неравенств в общем виде, решить одно из неравенств и оформить его по образцу. Решить анаграмму.	5 мин

Записать исходя из таблицы все случаи возможных решений неравенств в общем виде, решить одно несколько неравенств

Оформить домашнюю работу нужно по следующему образцу:

Решить анаграмму

АТВНСВЕНРЕ ЕНЕЕРИШ – анаграмма

Каждому лист с домашней работой, делаем группами. Образцы каждому ученику.

Здоровье сберегающая пауза.(1 мин)
Расслабимся не отходя от математики:

1. Покажите направление ветвей параболы, если старший коэффициент параболы а>0 ,а<0

2. Покажите главное направление оси абсцисс левой рукой, а оси ординат правой рукой. Теперь покажите это быстро.

3. Перед вами два магнита, посмотрите, не поворачивая головы, на магнит и на затылок соседа.

Из-за маленькой ошибки

Вижу ваши я улыбки

Ничего! Получится!

Ведь не делает ошибки,

Кто совсем не учится.

$c:\users\user\pictures\mp navigator\2013_11_24\img.jpg$

Приложение! (каждому ученику на парту)

Как по графику квадратичной функции определить знаки коэффициентов квадратного трехчлена

Чтобы определить знаки коэффициентов квадратного трехчлена по графику квадратичной функции, нужно вспомнить теорему Виета.

Согласно теореме Виета, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.

х₁+х₂=-b/а

x₁*x₂=c/а

По графику квадратичной функции мы легко можем определить знак коэффициента a – если ветви параболы направлены вверх, то a>0 , а если вниз, то a<0 .

Также по графику легко определяются знаки корней (корни квадратного трехчлена ax²+bx+c – это абсциссы точек пересечения графика функции y= ax²+bx+c с осью абсцисс), а также знак корня с большим модулем.

Если оба корня положительны, то х₁+х₂=-b>0 .

Если оба корня отрицательны, то х₁+х₂=-b<0.

Если корень с большим модулем положителен, то х₁+х₂=-b>0 .

Если корень с большим модулем отрицателен, то х₁+х₂=-b<0 .

Если корни имеют одинаковые знаки, то x₁*x₂=c >0 .

Если корни имеют разные знаки, то x₁*x₂=c <0.

Алгоритм решения неравенств второй степени с одной переменной:

Чтобы решить неравенства вида

ах² + вх + с > 0 и ax² + вx + c < 0 надо:

1.Найти дискриминант квадратного трехчлена и его корни

2.Отметить корни на оси х

3.Через отмеченные точки провести параболу, «ветви» которой направлены

- вверх, если а > 0,

- вниз, если a < 0

4. Если корней нет, то параболу изобразить

в верхней полуплоскости при а > 0

в нижней полуплоскости при а < 0

5.Для неравенства ах² + вх +с>0 сделать штриховку над осью х

6.Для неравенства ах² + вх +с<0 сделать штриховку под осью х

7. Заштрихованные промежутки записать в ответ

(каждому ученику на парту)