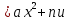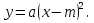|
Пояснительная записка. Статус документа Настоящая рабочая учебная программа базового курса «Алгебра» для 9 класса II ступени образования моу «Гостищевская средняя общеоб-разовательная школа Яковлевского района Белгородской области»
Пояснительная записка.
Статус документа
Настоящая рабочая учебная программа базового курса «Алгебра» для 9 класса II ступени образования МОУ «Гостищевская средняя общеоб-разовательная школа Яковлевского района Белгородской области» состав-лена на основе федерального компонента государственного образователь-ного стандарта базового уровня образования, утвержденного приказом Министерства образования РФ от 09.03.2004г. № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для общеобразовательных учреждений РФ, реализующих программы общего образования» и авторской программы по алгебре Ю. Н. Макарычева входящей в сборник программ «Программы общеобразовательных учреждений: Алгебра, 7-9 классы», составитель: Бурмистрова Татьяна Антоновна «Программы общеобразовательных учреждений: Алгебра , 7-9 классы».- М. Просвещение, 2008. При составлении рабочей программы учтены рекомендации инструктивно-методического письма «О преподавании математики 2011-2012 учебном году в общеобразовательных учреждениях Белгородской области».
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам об-разовательного процесса получить представление о целях, содержании, об-щей стратегии обучения, воспитания и развития учащихся средствами дан-ного учебного предмета.
Организационно-планирующая функция предусматривает выделение эта-пов обучения, структурирование учебного материа�ла, определение его коли-чественных и качественных характери�стик на каждом из этапов, в том числе для содержательного на�полнения промежуточной аттестации учащихся.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану для образова-тельных учреждений Российской Федерации на изучение алгебры в 9 классе отводится 3 ч в неделю. Планирование учебного материала по алгебре рас-считано на 102 учебных часа, количество контрольных работ: 10. Рабочая про-грамма конкретизирует содержание предметных тем образовательного стан-дарта и дает распределение учебных часов по разделам курса.
Изменения, внесенные в авторскую учебную программу и их обоснование:
В соответствии с планом внутришкольного контроля добавлены две контрольные работы: входная контрольная работа (за курс алгебры 8 класса) и административная контрольная работа (итоговая за I полугодие), также запланировано на 4 часа пробный экзамен, за курс основной школы. В связи с этим, изменено соотношение часов на раздел «Повторение», и вместо предложенных в авторской программе 21-го часа, в рабочей программе 15 часов.
Цели
Изучение математики на ступени основного общего образова�ния направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке нау-ки, средстве моделирования явлений и процессов, об идеях и методах мате-матики;
развитие логического мышления, пространственного воображения, алгорит-мической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в школе;
овладение математическими знаниями и умениями, необходимыми в пов-седневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значи-мости математики для научно-технического прогресса, отношения к мате-матике как к части общечеловеческой культуры через знакомство с исто-рией развития математики, эволюцией математических идей.
Задачи учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алг-ебра; геометрия; элементы ком�бинаторики, теории вероятностей, стати-стики и логи�ки. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечествен-ной и зарубежной школы и позволяют реализовать по�ставленные перед школьным образованием цели на информаци�онно емком и практически зна-чимом материале. Эти содер�жательные компоненты, развиваясь на протя-жении всех лет обучения, естественным образом переплетаются и взаи-модейству�ют в учебных курсах.
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выра-жений и формул;
совершенствование практических навыков и вычислительной культуры; приобретение прак�тических навыков, необходимых для повседневной жизни;
формирование математического аппа�рата для решения задач из математики, смежных предметов, окружающей реальности;
развитие алгоритмического мышле�ния, необходимого, в частности, для ос-воения курса информати�ки; овладение навыками дедуктивных рассуж-дений;
развитие воображения, способностей к математическому творче�ству;
важной задачей изучения алгебры является получе�ние школьниками кон-кретных знаний о функциях как важней�шей математической модели для описания и исследования разнообразных процессов (равномерных, равно-ускоренных, экс�поненциальных, периодических и др.), для формирования у уча�щихся представлений о роли математики в развитии цивилиза�ции и культуры;
формирование функциональной грамотности — умений вос�принимать и анализировать информацию, представленную в различных формах, пони-мать вероятностный характер многих реальных зависимостей, производить простейшие вероятност�ные расчеты в простейших прикладных задачах.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овла-девают разнообразными способами деятельности, приобретают и совер-шенствуют опыт:
планирования и осуществления алгоритмической деятельно�сти, выполне-ния заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов ре�шения;
исследовательской деятельности, развития идей, проведения экс�пери-ментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в уст�ной и письмен-ной речи, использования различных языков мате�матики (словесного, симво-лического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпре�тации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, вы�движения гипо-тез и их обоснования;
поиска, систематизации, анализа и классификации информа�ции, исполь-зования разнообразных информационных источни�ков, включая учебную и справочную литературу, современные информационные технологии.
Учебно-методический комплект
Алгебра: Учеб. Для 9 кл. общеобразовательных учреждений /Ю.Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под. ред. С. А. Теляковского. – М.: Просвещение, 2011.
Программы общеобразовательных учреждений: «Алгебра, 7-9 классы». Составитель: Бурмистрова Татьяна Антоновна - М. Просвещение, 2008.
Требования к уровню подготовки выпускников.
В результате изучения математики на базовом уровне ученик должен
знать/понимать
существо понятия математического доказательства; приво�дить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов; как ис-пользуются математические формулы, уравнения и не�равенства;
примеры их применения для решения математиче�ских и практических задач;
как математически определенные функции могут описывать реальные зависимости;
приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающе�го мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утвержде�ний о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры оши�бок, возникающих при идеализации.
Арифметика
уметь
выполнять устно арифметические действия: сложение и вы�читание двуз-начных чисел и десятичных дробей с двумя зна�ками, умножение однозна-чных чисел, арифметические опера�ции с обыкновенными дробями с одно-значным знаменателем и числителем.
переходить от одной формы записи чисел к другой, представ�лять десятич-ную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в ви�де дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки.
выполнять арифметические действия с рациональными числа�ми, сравни-вать рациональные и действительные числа; нахо�дить в несложных случаях значения степеней с целыми показа�телями и корней; находить значения числовых выражений; округлять целые числа и десятичные дроби, находить при�ближения чисел с недостатком и с избытком, выполнять оценку числовых выражений.
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные едини�цы через более мелкие и наоборот.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с исполь-зованием при необходимости справочных мате�риалов, калькулятора, ком-пьютера; устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов; интер-претации результатов решения задач с учетом ограниче�ний, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
составлять буквенные выражения и формулы по условиям за�дач; осуще-ствлять в выражениях и формулах числовые под�становки и выполнять соответствующие вычисления, осуще�ствлять подстановку одного выра-жения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показа�телями, с многочленами и с алгебраическими дробями; вы�полнять разложение мно-гочленов на множители;
выполнять тождественные преобразования рациональных выражений; при-менять свойства арифметических квадратных корней для вычисления зна-чений и преобразований числовых выраже�ний, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сво-дящиеся к ним, системы двух линейных урав�нений и несложные нелиней-ные системы;
решать линейные и квадратные неравенства с одной перемен�ной и их сис-темы;
решать текстовые задачи алгебраическим методом, интерпре�тировать полу-ченный результат, проводить отбор решений, исходя из формулировки за-дачи;
изображать числа точками на координатной прямой; определять корд-инаты точки плоскости, строить точки с за�данными координатами; изо-бражать множество решений ли�нейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и сум�мы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей; определять свойства функции по ее графику; при-менять гра�фические представления при решении уравнений, систем, не�ра-венств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, вы�ражающих зависимости между реальными величинами; нахо�ждения нужной формулы в справочных материалах; моделирования практических ситуаций и иссле-дования по�строенных моделей с использованием аппарата алгебры; опии-сания зависимостей между физическими величинами со�ответствующими формулами при исследовании несложных практических ситуаций; интер-претации графиков реальных зависимостей между вели�чинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использо�вать примеры для иллюстрации и контрпримеры для опровер�жения утверждений;
извлекать информацию, представленную в таблицах, на диа�граммах, гра-фиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического пере�бора возмож-ных вариантов и с использованием правила умно�жения;
вычислять средние значения результатов измерений; находить частоту события, используя собственные наблюде�ния и готовые статистические данные;
находить вероятности случайных событий в простейших слу�чаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве и в диалоге; распоз-навания логически некорректных рассуждений; записи математических утверждений, доказательств; анализа реальных числовых данных, пред-ставленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессио�нальной деятель-ности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости; решения учебных и практических задач, тре-бующих система�тического перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических си�туациях, сопоставления модели с реальной ситуацией; понимания статистических утверждений.
Календарно-тематическое планирование.
№ п\п
|
Наименование
раздела и тем
|
Часы учеб-ного вре-мени
|
План. дата прове-дения
|
Дата факт. прове-дения
|
Примеча-ние
|
1.
|
Глава I. Квадратичная функция.
|
22+1
|
|
|
|
1.
|
Функции и их свойства. Функция. Область определения и область значений функции.
|
1
|
|
|
|
2.
|
Функция. Область определения и область значений функции.
|
1
|
|
|
|
3.
|
Свойства функций.
|
1
|
|
|
Подг. К ГИА
5.1.1
|
4.
|
Свойства функций.
|
1
|
|
|
|
5.
|
Свойства функций.
Самостоятельная работа №1.
|
1
|
|
|
|
6.
|
Квадратный трехчлен.
Квадратный трехчлен и его корни.
|
1
|
|
|
|
7.
|
Квадратный трехчлен и его корни.
|
1
|
|
|
|
8
|
Входная контрольная работа № 1 за курс 8 класса.
|
1
|
|
|
|
9.
|
Разложение квадратного трехчлена на множители.
|
1
|
|
|
|
10.
|
Разложение квадратного трехчлена на множители.
|
1
|
|
|
Подг. К ГИА
2.3.4
|
11.
|
Контрольная работа №2
«Квадратный трехчлен».
|
1
|
|
|
|
12.
|
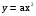 Квадратичная функция и ее график. Квадратичная функция и ее график.
Функция
ее график и свойства.
|
1
|
|
|
|
13.
|
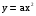 Функция Функция
ее график и свойства.
|
1
|
|
|
|
14.
|
Графики функций
у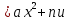
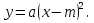
|
1
|
|
|
|
15.
|
Графики функций
у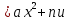
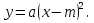
|
1
|
|
|
Подг. К ГИА
5.1.2
|
16.
|
Построение графика квадратичной функции.
|
1
|
|
|
|
17.
|
Построение графика квадратичной функции.
|
1
|
|
|
|
18.
|
Построение графика квадратичной функции.
|
1
|
|
|
Подг. К ГИА
5.1.7
|
19.
|
Построение графика квадратичной функции. Самостоятельная работа №2.
|
1
|
|
|
|
20.
|
Степенная функция. корень n-ой степени. Функция у= хп.
Корень n-ой степени.
|
1
|
|
|
|
21.
|
Дробно-линейная функция и ее график.
|
1
|
|
|
|
22.
|
Степень с рациональным показателем.
|
1
|
|
|
|
23.
|
Контрольная работа №3
«Квадратичная функция и ее график».
|
1
|
|
|
|
2.
|
Глава II. Уравнения и неравенства с одной переменной.
|
14+4
|
|
|
|
24.
|
Уравнения с одной переменной. Целое уравнение и его корни.
|
1
|
|
|
|
25.
|
Целое уравнение и его корни.
|
1
|
|
|
|
26.
|
Целое уравнение и его корни.
|
1
|
|
|
|
27.
|
Целое уравнение и его корни.
|
1
|
|
|
|
28-31
|
Пробный экзамен за курс основной школы
|
4
|
|
|
|
32.
|
Дробные рациональные уравнения.
|
1
|
|
|
|
33.
|
Дробные рациональные уравнения. Самостоятельная работа №3.
|
1
|
|
|
|
34.
|
Дробные рациональные уравнения.
|
1
|
|
|
|
35.
|
Дробные рациональные уравнения.
|
1
|
|
|
|
36.
|
Неравенства с одной переменной. Решение неравенств второй степени с одной переменной.
|
1
|
|
|
|
37.
|
Решение неравенств второй степени с одной переменной.
|
1
|
|
|
|
38.
|
Решение неравенств методом интервалов.
|
1
|
|
|
|
39.
|
Решение неравенств методом интервалов.
|
1
|
|
|
|
40.
|
Решение неравенств методом интервалов.
|
1
|
|
|
|
41.
|
Контрольная работа №4 «Уравнения и неравенства с одной переменной».
|
1
|
|
|
|
3.
|
Глава III. Уравнения и неравенства с двумя переменными.
|
17+1
|
|
|
|
42.
|
Уравнения с двумя переменными и их системы. Уравнение с двумя переменными и его график.
|
1
|
|
|
|
43.
|
Уравнение с двумя переменными и его график.
|
1
|
|
|
|
44.
|
Графический способ решения систем уравнений.
|
1
|
|
|
|
45.
|
Графический способ решения систем уравнений.
|
1
|
|
|
|
46.
|
Графический способ решения систем уравнений.
|
1
|
|
|
|
47.
|
Графический способ решения систем уравнений. Самостоятельная работа №4.
|
1
|
|
|
|
48.
|
Решение систем уравнений второй степени.
|
1
|
|
|
|
49.
|
Решение систем уравнений второй степени.
|
1
|
|
|
|
50.
|
Решение систем уравнений второй степени.
|
1
|
|
|
|
51.
|
Решение систем уравнений второй степени.
|
1
|
|
|
|
52.
|
Решение задач с помощью уравнений второй степени.
|
1
|
|
|
|
53.
|
Решение задач с помощью уравнений второй степени.
|
1
|
|
|
|
54.
|
Административная контрольная работа №5.
|
1
|
|
|
|
55.
|
Неравенства с двумя переменными и их системы. Неравенства с двумя переменными.
|
1
|
|
|
|
56.
|
Неравенства с двумя переменными.
|
1
|
|
|
|
57.
|
Системы неравенств с двумя переменными.
|
1
|
|
|
|
58.
|
Системы неравенств с двумя переменными.
|
1
|
|
|
|
59.
|
Контрольная работа №6 «Уравнения и неравенства с двумя переменными».
|
1
|
|
|
|
4.
|
Глава IV. Арифметическая и геометрическая прогрессии.
|
15
|
|
|
|
60.
|
Арифметическая прогрессия. Последовательности.
|
1
|
|
|
|
61.
|
Последовательности.
|
1
|
|
|
|
62.
|
Определение арифметической прогрессии Формула n-го члена арифметической про�грессии.
|
1
|
|
|
|
63.
|
Определение арифметической прогрессии Формула n-го члена арифметической про�грессии.
|
1
|
|
|
|
64.
|
Формула суммы п первых членов арифмети�ческой прогрессии.
|
1
|
|
|
|
65.
|
Формула суммы п первых членов арифмети�ческой прогрессии.
|
1
|
|
|
|
66.
|
Формула суммы п первых членов арифмети�ческой прогрессии.
|
1
|
|
|
|
67.
|
Контрольная работа №7 «Арифметическая прогрессия».
|
1
|
|
|
|
68.
|
Геометрическая прогрессия. Определение геометрической прогрессии. Формула n-го члена геометрической про�грессии.
|
1
|
|
|
|
69.
|
Определение геометрической прогрессии. Формула n-го члена геометрической про�грессии.
|
1
|
|
|
|
70.
|
Формула суммы п первых членов геометри�ческой прогрессии.
|
1
|
|
|
|
71.
|
Формула суммы п первых членов геометри�ческой прогрессии.
|
1
|
|
|
|
72.
|
Формула суммы п первых членов геометри�ческой прогрессии.
|
1
|
|
|
|
73.
|
Формула суммы п первых членов геометри�ческой прогрессии.
|
1
|
|
|
|
74.
|
Контрольная работа №8 «Геометрическая прогрессия».
|
1
|
|
|
|
5.
|
ГлаваV. Элементы комбинаторики и теории вероятностей.
|
13
|
|
|
|
75.
|
Элементы комбинаторики.
Примеры комбинаторных задач.
|
1
|
|
|
|
76.
|
Примеры комбинаторных задач.
|
1
|
|
|
|
77.
|
Перестановки.
|
1
|
|
|
|
78.
|
Перестановки.
|
1
|
|
|
|
79.
|
Размещения.
|
1
|
|
|
|
80.
|
Размещения.
|
1
|
|
|
|
81.
|
Сочетания.
|
1
|
|
|
|
82.
|
Сочетания.
|
1
|
|
|
|
83.
|
Сочетания.
|
1
|
|
|
|
84.
|
Начальные сведенья из теории вероятностей. Относительная частота случайного события.
|
1
|
|
|
|
85.
|
Вероятность равновозможных событий.
|
1
|
|
|
|
86.
|
Вероятность равновозможных событий.
|
1
|
|
|
|
87.
|
Контрольная работа №9 «Элементы комбинаторики и теории вероятностей».
|
1
|
|
|
|
5.
|
Повторение.
|
11
|
|
|
|
88.
|
Квадратичная функция.
|
1
|
|
|
|
89.
|
Квадратичная функция.
|
1
|
|
|
|
90.
|
Уравнения и неравенства с одной переменной.
|
1
|
|
|
|
91.
|
Уравнения и неравенства с одной переменной.
|
1
|
|
|
|
92.
|
Уравнения с двумя переменными и их системы.
|
1
|
|
|
|
93.
|
Уравнения с двумя переменными и их системы.
|
1
|
|
|
|
94.
|
Арифметическая прогрессия.
|
1
|
|
|
|
95.
|
Геометрическая прогрессия.
|
1
|
|
|
|
96.
|
Геометрическая прогрессия.
|
1
|
|
|
|
97.
|
Элементы комбинаторики и теории вероятностей.
|
1
|
|
|
|
98.
|
Системы уравнений.
|
1
|
|
|
|
99.
|
Итоговая контрольная работа№10.
|
1
|
|
|
|
100.
|
Функции. Решение задач.
|
1
|
|
|
|
101.
|
Прогрессии. Решение упражнений.
|
1
|
|
|
|
102.
|
Обобщающий урок за курс 9-го класса.
|
1
|
|
|
|
|
Итого
|
102 ч
|
|
|
|
Содержание программы учебного курса
Свойства функций. Квадратичная функция
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция 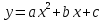 , её свойства и график. Степенная функция. , её свойства и график. Степенная функция.
Основная цель – расширить сведения о свойствах функций, озна-комить обучающихся со свойствами и графиком квадратичной функции.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, гра-фик. Даются понятия о возрастании и убывании функции, промежутках зна-копостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квад�ратного трехчлена, разложении квад-ратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции 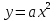 , её свойств и особенностей графика, а также других частных видов квадратичной функции – функции , её свойств и особенностей графика, а также других частных видов квадратичной функции – функции 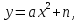 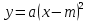 . Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции . Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции 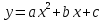 может быть получен из графика функции может быть получен из графика функции 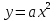 с помощью двух парал-лельных переносов. Приёмы построения графика функции с помощью двух парал-лельных переносов. Приёмы построения графика функции
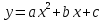 отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей пара-болы. отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей пара-болы.
Учащиеся знакомятся со свойствами степенной функции 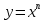 при четном и нечетном натуральном показателе n. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида при четном и нечетном натуральном показателе n. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида 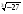 , , 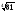 . Они получают представление о нахождении значений корня с помощью кальку-лятора, причем выработка соответствующих умений не требуется. . Они получают представление о нахождении значений корня с помощью кальку-лятора, причем выработка соответствующих умений не требуется.
Уравнения и неравенства с одной переменной
Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.
Основная цель — систематизировать и обобщить сведения о реше-нии целых и дробных рациональных уравнений с одной переменной, сформи-ровать умение решать неравенства,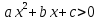 , , 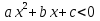 , ,
где а 0. 0.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Учащиеся знакомятся с решением уравнений третьей степени и четвертой с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
Расширяются сведения о решении дробных рациональных уравнений. Учащиеся знакомятся с некоторыми специальными приемами решения таких уравнений.
Формирование умение решать неравенства,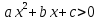 , , 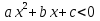 , где а , где а 0, осуществляется с опорой на сведенья о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох). 0, осуществляется с опорой на сведенья о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох).
Учащиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
Уравнения и неравенства с двумя переменными
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Основная цель — выработать умение решать простейшие системы содержащие уравнение второй степени с двумя переменными , и текстовые задачи с помощью составления таких систем.
В данной теме завершается изучение систем уравнений с двумя переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный учащимся способ подстановки находит здесь дальнейшее применение.
Ознакомление учащихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных учащимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно пока учащимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач решаемых с помощью систем уравнений.
Изучение темы завершается введением понятий неравенств с двумя переменными и системы неравенств с двумя переменными. Сведения о гра-фиках уравнений с двумя переменив, используются при иллюстрации мно-жеств решений некоторых простейших неравенств с двумя переменными и их систем.
Прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Основная цель – дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
При изучении темы вводится понятие последовательности, разъяс-няется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомо-гательный характер и используются для изучения арифметической и геоме-трической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и гео-метрической прогрессий, что позволяет расширить круг предлагаемых задач.
Степенная функция. Корень n -й степени
Четная и нечетная функция. Функция 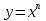 . Определение корня n-й степени. Вычисление корней n -й степени. . Определение корня n-й степени. Вычисление корней n -й степени.
Основная цель – ввести понятие корня n -й степени.
В данной теме продолжается изучение свойств функций: вводятся по-нятия четной и нечетной функции, рассматрива�ются свойства степенной функции с натуральным показателем. Изучение корней ограничивается вве-дением понятия корня n-й степени и выполнением несложных заданий на вычисление корней n-й степени, в частности кубических корней.
Свойства корней n-й степени, понятие степени с рациональным показателем и ее свойства не изучаются. Этот материал будет рассмотрен в старшей школе.
Элементы комбинаторики и теории вероятностей
Комбинаторное правило умножения. Перестановки, размеще�ния, соче-тания. Относительная частота и вероятность случайного события.
Основная цель – ознакомить обучающихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, раз-мещений и сочетаний. При изучении данного материала необходимо обра-тить внимание обучающихся на различие понятий «размещение» и «соче-тание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме обучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относи-тельная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности слу-чайного события. Важно обратить внимание обучающихся на то, что класс-сическое определение вероятности можно применять только к таким моде-лям реальных событий, в которых все исходы являются равновозможными.
Повторение
Основная цель – повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.
|
|
|
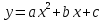 , её свойства и график. Степенная функция.
, её свойства и график. Степенная функция.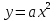 , её свойств и особенностей графика, а также других частных видов квадратичной функции – функции
, её свойств и особенностей графика, а также других частных видов квадратичной функции – функции 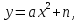
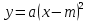 . Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции
. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции 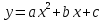 может быть получен из графика функции
может быть получен из графика функции 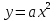 с помощью двух парал-лельных переносов. Приёмы построения графика функции
с помощью двух парал-лельных переносов. Приёмы построения графика функции 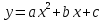 отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей пара-болы.
отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей пара-болы.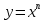 при четном и нечетном натуральном показателе n. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида
при четном и нечетном натуральном показателе n. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида 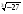 ,
, 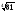 . Они получают представление о нахождении значений корня с помощью кальку-лятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью кальку-лятора, причем выработка соответствующих умений не требуется.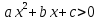 ,
, 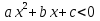 ,
, 0.
0.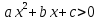 ,
, 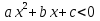 , где а
, где а 0, осуществляется с опорой на сведенья о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох).
0, осуществляется с опорой на сведенья о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох).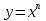 . Определение корня n-й степени. Вычисление корней n -й степени.
. Определение корня n-й степени. Вычисление корней n -й степени. Скачать
Скачать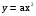 Квадратичная функция и ее график.
Квадратичная функция и ее график. 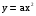 Функция
Функция