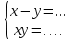Урока : формировать умение решать задачи «на работу»
 Скачать 90.39 Kb. Скачать 90.39 Kb.
|
| Урок математики (алгебры) в 9 классе по теме: «Решение задач с помощью систем уравнений второй степени». Цель урока: формировать умение решать задачи «на работу» составлением систем уравнений; Задачи:
Форма проведения урока: урок формирования умений и навыков. Оборудование: презентация, раздаточный материал. План урока.
А) Решение систем уравнений. Б) Математический диктант
Ход урока. 1.Организационный момент. Вместе с дежурными учитель проверяет готовность класса к уроку.
2.Проверка домашнего задания. А)Проверка домашнего задания осуществляется в виде самостоятельной работы по вариантам. При решении учащиеся 1 и 2 вариантов могут воспользоваться карточками- консультантами. (Эти варианты для учащихся с низким уровнем математической подготовки)
Ответ: x = 1; y = 2.
Ответ: x = 3; y = 0.
Ответ: ( -7; -8 ); ( 5; 4 ). Карточки-консультанты:
Слайд 3.  Б) Математический диктант. Ученики делают диктант под копировку. Копию работы оставляют себе для самопроверки. Два ученика выполняют диктант у доски по вариантам. 1. Система уравнений второй степени - это …(два и более уравнений, которыми можно манипулировать для нахождения общих решений). 2. Решением системы уравнений второй степени называют … (пару значений переменных, обращающую каждое из уравнений системы в верное равенство) 3. Решить систему уравнений второй степени значит … (найти все её решения или доказать, что этих решений нет) 4. Равносильные системы уравнений - это … (системы, имеющие одни и те же решения) 5. Какие основные способы решения систем уравнений вы знаете? (Способ подстановки, способ сложения, графический способ) 6. Подберите наиболее подходящий метод для решения следующих систем уравнений: 1) 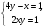 ; 2) ; 2) 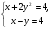 ; 3) ; 3) 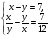 ; 4) ; 4) 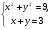 ; 5) ; 5) 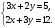 Слайд 4  (1 - подстановка; 2 – сложением; 3 – подстановка; 4 – графически; 5 – сложением) Самопроверка с доски, обсуждение результатов (по необходимости) 3.Актуализация знаний. Для подготовки учащихся к решению задач повторяются и систематизируются их знания. Решение задач состоит из трёх этапов:
Каждый из этих этапов является важным в решении задачи. Слайд 5  Задачи, в которых кто-то выполняет некоторую работу, или задачи, связанные с наполнением или опорожнением резервуаров, напоминают задачи «на движение». В задачах такого типа вся работа или полный объем резервуара аналогичны роли расстояния в задачах «на движение», а производительности выполняющих работу объектов аналогичны скоростям движения. Часто объем работы в таких задачах не указывается и не является искомым. В таких случаях объем всей работы удобно принимать за единицу. Давайте вспомним, какими величинами характеризуется данный процесс - совместная работа.
Совместная производительность – это часть работы, выполненная за 1 единицу времени вместе всеми участниками. Формулы: А= Р . t , при А=1, Р=1/t Слайд 6  4.Изучение нового материала. Решение задач. А) Ученик решает на доске № 279. [1] Примем всю работу за 1. Пусть первый экскаватор, работая один, выполнит всю работу за x часов, а второй – за y часов.
y-x=4
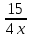 + + 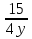 = 1 = 13 ч 45 мин = 3 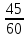 ч = 3 ч = 3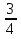 ч = ч = 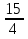 ч чТаким образом, получим систему уравнений: 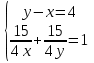 Выберите способ решения системы уравнений. (Подстановка) 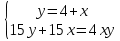 ; ;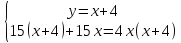 ; ;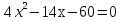 , , 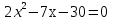 , , D=289, X1= - 2,5, не удовлетворяет условию x 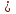 0; 0;X2=6 Решением системы будет пара чисел 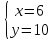 Ответ: 6 часов, 10 часов. Обсуждение, уточнение хода решения. Алгоритм:
Слайд 7  Б) Задача №325 на доске и в тетрадях Работа по алгоритму:
Из данной таблицы видно, что принято за х, за y, какова производительность каждой трубы. Составим первое уравнение на основании того, что одна вторая труба могла наполнить бассейн в 1, 5 раза быстрее, чем одна первая. х=1,5у
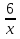 + + 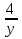 = 1 = 1Имеем систему уравнений: 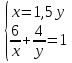 ; ; 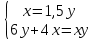 ; ; 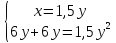 24y - 3y2=0; 3y(8 – y)=0; y1=0, не удовлетворяет условию y 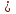 0; 0;y2=8. Таким образом, 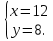 Ответ: 12 часов, 8 часов. 5.Самостоятельная работа. При решении работы учащиеся могут воспользоваться карточками-консультантами. 1 вариант. Разность двух чисел равна 5, а их произведение 84. Найдите эти числа. 2 вариант. Разность двух натуральных чисел равна 24, а их произведение равно 481. Найдите эти числа. Слайд 8  Карточки-консультанты к самостоятельной работе.
6.Итог урока. Рефлексия. В конце урока оцениваются ответы учащихся у доски и самостоятельные работы. Ещё раз обращается внимание учащихся на 3 этапа и алгоритм решения данных задач. Учащимся предлагается оценить, что было самым интересным, самым легким, самым трудным. 7.Задание на дом. № 280, 324, 288 (б,г). [1] Список литературы:
|


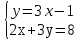 ;
;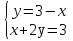 ;
;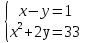 ;
;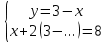 ;
;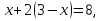
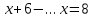 ,
,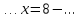 ,
,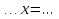 ,
, ,
,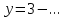 ,
,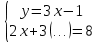 ;
;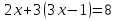 ,
,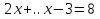 ,
,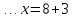 ,
,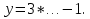
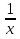
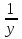
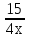
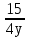
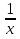 , второй трубы -
, второй трубы -