7.Материально-техническое обеспечение учебного предмета.
Основная литература:
Математика.5 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М., 2012.
Дополнительная литература:
Жохов, В. И. Математика. 5-6 классы. Программа. Планирование учебного материала /
И. Жохов. - М.: Мнемозина, 2011.
Жохов, В. И. Преподавание математики в 5 и 6 классах: методические рекомендации для учителя к учебнику Виленкина Н. Я. [и др.] / В. И. Жохов. - М.: Мнемозина, 2008.
Жохов, В. И. Математика. 5 класс. Контрольные работы для учащихся / В. И. Жохов, JI. Б. Крайнева. - М.: Мнемозина, 2011.
Жохов, В. И. Математические диктанты. 5 класс : пособие для учителей и учащихся / В. И. Жохов, И. М. Митяева. М.: Мнемозина, 2011.
Жохов, В. Я Математический тренажер. 5 класс: пособие для учителей и учащихся / В. И. Жохов, В. Н. Погодин. - М: Мнемозина, 2011.
Рудницкая, В. Н. Математика. 5 класс. Рабочая тетрадь № 1 : учебное пособие для обра�зовательных учреждений / В. Н. Рудницкая. - М.: Мнемозина, 2011.
Рудницкая, В. Я Математика. 5 класс. Рабочая тетрадь № 2 : учебное пособие для обра�зовательных учреждений / В. Н. Рудницкая. - М: Мнемозина, 2011.
Учебное интерактивное пособие к учебнику Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда «Математика. 5 класс»: тренажер по математике. М: Мнемози�на, 2010.
А.П.Ершова, В.В.Голобородько « Математика класс» : самостоятельные и контрольные работы. М.»ИЛЕКСА» 2003
Специфическое сопровождение (оборудование)
классная доска с набором магнитов для крепления таблиц;
средства обучения( предписания, схемы, алгоритмы, памятки);
персональный компьютер;
мультимедийный проектор;
демонстрационные измерительные инструменты и приспособления (размеченные и неразмеченные линейки, циркули, транспортиры, наборы угольников, мерки);
демонстрационные пособия для изучения геометрических величин ( длины, периметра, площади): палетка, квадраты (мерки) и др.;
демонстрационные пособия для изучения геометрических фигур: модели геометрических фигур и тел, развертки геометрических тел;
демонстрационные таблицы.
Информационное сопровождение:
Сайт ФИПИ;
Сайт газеты «Первое сентября»;
Сайт «uztzt».
Сайт « Учительский портал»
Школа Цифрового века
8.Предметные результаты:
Натуральные числа. Дроби. Рациональные числа.
Ученик научится:
понимать особенности десятичной системы счисления;
сравнивать и упорядочивать натуральные числа;
выполнять вычисления с натуральными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные процентами, в ходе решения математических задач, выполнять несложные практические расчёты.
Ученик получит возможность:
познакомиться с позиционными системами счисленияс основаниями, отличными от 10;
углубить и развить представления о натуральных числах;
научиться использовать приёмы, рационализирующиевычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Измерения, приближения, оценки
Ученик научится:
использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Ученик получит возможность:
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения.
Уравнения
Ученик научится:
решать простейшие уравнения с одной переменной;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
Ученик получит возможность:
овладеть специальными приёмами решения уравнений;
уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
Неравенства
Ученик научится:
понимать и применять терминологию и символику, связанные с отношением неравенства;
применять аппарат неравенств, для решения задач.
Ученик получит возможность научиться:
уверенно применять аппарат неравенств, для решения разнообразных математических задач и задач из смежных предметов, практики;
Описательная статистика.
Ученик научится использовать простейшие способы представления и анализа статистических данных.
Ученик получит возможность:
приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, представлять результаты опроса в виде таблицы, диаграммы.
Комбинаторика
Ученик научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Ученик получит возможность :
научиться некоторым специальным приёмам решения комбинаторных задач.
Наглядная геометрия
Ученик научится:
распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
распознавать развёртки куба, прямоугольного параллелепипеда;
строить развёртки куба и прямоугольного параллелепипеда;
вычислять объём прямоугольного параллелепипеда.
Ученик получит возможность:
научиться вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;
углубить и развить представления о пространственных геометрических фигурах.
Геометрические фигуры
Ученик научится:
пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
находить значения длин линейных фигур, градусную меру углов от 0 до 180°;
решать несложные задачи на построение.
Ученик получит возможность:
научится пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
находить значения длин линейных фигур, градусную меру углов от 0 до 180°;
решать несложные задачи на построение.
Измерение геометрических величин
Ученик научится:
использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, градусной меры угла;
вычислять площади прямоугольника, квадрата;
вычислять длины линейных элементов фигур и их углы, формулы площадей фигур;
решать задачи на применение формулы площади прямоугольника, квадрата.
Ученик получит возможность научиться:
использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, градусной меры угла;
вычислять площади прямоугольника, квадрата;
вычислять длины линейных элементов фигур и их углы, формулы площадей фигур;
решать задачи на применение формулы площади прямоугольника, квадрата.
Координаты
Ученик научится:
находить координаты точки.
Ученик получит возможность:
овладеть координатным методом решения задач.
Работа с информацией
Ученик научится:
заполнять простейшие таблицы по результатам выполнения практической работы, по рисунку;
выполнять действия по алгоритму;
читать простейшие круговые диаграммы.
Ученик получит возможность научиться:
устанавливать закономерность расположения данных в строках и столбцах таблицы, заполнять таблицу в соответствии с установленной закономерностью;
понимать информацию, заключенную в таблице, схеме, диаграмме и представлять ее в виде текста (устного или письменного), числового выражения, уравнения;
выполнять задания в тестовой форме с выбором ответа;
выполнять действия по алгоритму; проверять правильность готового алгоритма, дополнять незавершенный алгоритм;
строить простейшие высказывания с использованием логических связок «верно /неверно, что ...»;
составлять схему рассуждений в текстовой задаче от вопроса
Примечание.
Критерии оценивания
Контроль знаний учащихся осуществляется в виде контрольных работ (входная, промежуточная, итоговая) и зачетов (тесты).
Каждый зачет состоит из обязательной и дополнительной частей. Выполнение каждого задания обязательной части оценивается одним баллом. Оценка выполнения каждого задания дополнительной части приводится рядом с номером задания.
Общая оценка выполнения любого зачета (тест) осуществляется в соответствии с приведенной ниже таблицей
Отметка
|
«зачёт»
|
«4»
|
«5»
|
Обязательная часть
|
6 баллов
|
7 баллов
|
7 баллов
|
Дополнительная часть
|
|
3 балла
|
5 баллов
|
Таблица показывает, сколько баллов минимум надо набрать при выполнении заданий обязательной и дополнительной частей для получения оценки «Зачет», «4», «5».
Обязательная часть зачетов направлена на проверку уровня базовой подготовки учащихся по математике.
Задания дополнительной части зачетов позволяют выявить знания учащихся на более высоком уровне.
Общая оценка выполнения контрольной работы осуществляется в соответствии с приведенной ниже таблицей
Отметка
|
«3»
|
«4»
|
«5»
|
Обязательная часть
|
3 задания (без задачи)
|
3 задания
|
4задания
|
Дополнительная часть
|
|
задача
|
задача
|
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
2. Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материалавыявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
3. Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Приложение 1
ВХОДНАЯ КОНТРОЛЬНАЯ РАБОТА
Вариант 1
Вычислите: 208896 : 68 + (10403 – 9896) • 204
Какая из величин больше и на сколько?
6 м 1 см или 61 дм 3 см
Решите уравнение 24 + 416 : х = 50.
Решите задачу.
Первый рабочий за 1 час делает 32 детали, а второй за 4 часа делает столь�ко же деталей, сколько первый за 5 часов. За сколько часов они сделают 216 де�талей при совместной работе?
На отрезке АМ= 22 см отметили точку К такую, что АК = 16 см, и точку Р такую, что РМ= 17 см. Найдите длину отрезка КР.
Вариант 2
Вычислите: (1142600 – 890778): 74 + 309 • 708.
Какая из величин больше и на сколько?
2 т 5 кг или 24 ц 1 кг
Решите уравнение 50-232 :x= 21.
Решите задачу.
Двум рабочим надо сделать 3600 деталей. Один рабочий может сделать эти детали за 20 часов, а оба рабочих, работая вместе, могут их сделать за 12 часов. За сколько часов все эти детали может сделать второй рабочий?
На отрезке АВ = 20 см отметили точку М такую, что AM = 17 см, и точку N такую, чтоBN – 16 см. Найдите длину отрезкаMN.
Приложение 2
ТЕСТ 1
Вариант 1
Выполните задания, ответьте на вопросы (верный ответ подчеркните).
Найдите верную запись числа три миллиона двадцать тысяч три.
а) 320 003; 6)3 023 000; в) 3 002 003; г) 3 020 003.
Расположите в порядке убывания числа 31 099, 310 001, 31 109.
а) 310 001, 31 109,31 099;
б) 310 001,31 099,31 109;
в) 31 109,31 099,310 001;
г) 31 099,31 109,310 001.
Найдите число, в котором 8 единиц второго класса.
а) 888; б) 8008; в) 800 008; г) 80 088.
Представьте число 56 270 в виде суммы разрядных слагаемых.
а) 56 000+200+70;
б) 50 000+6000+270;
в) 50 000+6000+200+70;
г) 56 000+270.
Какое из шестизначных чисел, записанных тройками и пятерками, явля�ется самым большим?
а) 553 533; 6) 533 553; в) 555 333; г) 535 353.
К какому числу надо прибавить единицу, чтобы получилось 190 000?
а) 18 999; б) 1899; в) 189 999; г) 180 999.
Запишите три раза подряд число 87 и три раза подряд число 13. Сложите полученные числа. Какой ответ получился в результате?
а) один миллион десять тысяч сто;
б) сто одна тысяча сто;
в) десять миллионов сто одна тысяча;
г) сто одиннадцать тысяч сто.
8*. На сколько отличается число 50000 + 4000 + 200 + 30 + 5 от числа
40000 + 3000 + 100 + 20 + 4?
а) на 1111; б)на 1; в) на 11; г) на 11111
Вариант 2
Найдите верную запись числа пятьдесят миллионов четыре тысячи девять.
а) 50 400 009; б) 50 004 009; в) 54 000 009; г) 50 040 090.
Расположите в порядке возрастания числа 732 001, 73 199, 73 204.
а) 73 204, 73 199, 732 001;
б) 73 199, 73 204, 732 001;
в) 732 001,73 204, 73 199;
г) 732 001,73 199, 73 204.
Найдите число, в котором 50 единиц второго класса.
а) 555; 6) 5550; в) 50 005; г) 500 500.
Представьте число 83 610 в виде суммы разрядных слагаемых.
а) 83 000 + 610;
б) 80 000 + 3000 + 600+ 10;
в) 80 000 + 3600+ 10;
г) 83 000 + 600 + 10.
Какое из шестизначных чисел, записанных четверками и девятками, явля�ется самым большим?
а) 949 494; б) 994 944; в) 999 444; г) 949 944.
К какому числу надо прибавить единицу, чтобы получилось 200 000?
а) 190 000; б) 199 099; в) 199 999; г) 19 999.
Запишите три раза подряд число 76 и три раза подряд число 24. Сложите полученные числа. Какой ответ получился в результате?
а) один миллион десять тысяч сто;
б) сто одна тысяча сто;
в) десять миллионов сто одна тысяча;
г) сто одиннадцать тысяч сто.
8*. На сколько отличается число 50000 + 8000 + 800 + 80 + 8 от числа
50000 + 7000 + 700 + 70 + 7?
а) на 1111; б) на1; в) на 11; г) на 11111.
Приложение 3
СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ
Вариант 1
Подчеркните верный ответ или предложите свой.
Число 1 - наименьшее натуральное число.
а) да; в) не знаю;
б) нет; г) свой ответ
Каждое натуральное число имеет последующее.
а) да; в) не знаю;
б) нет; г) свой ответ
Число 118 предшествует числу 119.
а) да; в) не знаю;
б) нет; г) свой ответ
В разряде сотен тысяч в записи числа 135 624 790 стоит цифра:
а) 2; в) 6;
б) 1; г) свой ответ
Результат сложения двух чисел называется:
а) разностью; в) суммой;
б) произведением; г) свой ответ
6. Если уменьшаемое 12 784, вычитаемое 9 386, то разность равна:
а) 22 170; в) 3398;
б) 3 389; г) свой ответ
7. При выполнении вычитания чисел 5 837 и 45 в столбик правильной является запись:
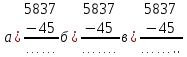 г) свой ответ г) свой ответ
Сумма чисел 7549 и 3451 равна:
а) 11 ООО; в) 4 098;
б) 10 990; г) свой ответ
При выполнении действий 104 560 + (30 567 - 30 040) получается:
а) 105 087; в) 165 167; б) 104 087;
г) свой ответ.
Переместительное свойство сложения для чисел 15 и 18 записывается гак:
а) 15+ 18 =15- 18; б) 15+ 18= 18-15;
в) 15 + 18= 18+ 15; г) свой ответ .
11. Свойство вычитания суммы из числа для числа 10 и суммы 3 и 1 записывается так:
а) 10-(3 + 1) = (10-3)-1; в) 10-(3 + 1)= 10-3 + 1;
б) (10 + 3) - 1 = 10 - (3 + 1); г) свой ответ
12*. Чему равна разность самого большого и самого маленького из чисел, составленных из цифр 1, 3 и 5? (В любом числе каждая цифра используется только один раз.)
а) 396; в) 777;
б)216; г) свой ответ
Вариант 2
Подчеркните верный ответ или предложите свой.
Ряд натуральных чисел бесконечен.
а) да; в) не знаю;
б) нет; г) свой ответ
Каждое натуральное число имеет предыдущее
а) да; в) не знаю;
б) нет; г) свой ответ
Число 400 следует за 309.
а) да; в) не знаю;
б) нет; г) свой ответ
В разряде десятков тысяч в записи числа 18 364 257 стоит цифра:
а) 1; в) 5;
б) 6; г) свой ответ
Результат вычитания двух чисел называется:
а) разностью; в) частным;
б) суммой; г) свой ответ
Если первое слагаемое 12 784, а второе слагаемое 9 386, то сумма равна:
а) 22 170; в) 3398;
б) 22 160; г) свой ответ
При выполнении сложения чисел 5 837 и 45 в столбик правильной является
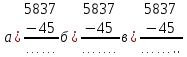 г)свой ответ г)свой ответ
Разность чисел 7549 и 3451 равна:
а) 4098; в) 4 198;
б) 11 ООО; г) свой ответ .
При выполнении действий 104 460 + (30 765 - 30 040) получается:
а) 105 185; в) 138 265;
б) 104 185; г) свой ответ
Сочетательное свойство сложения для чисел 3, 6 и 7 записывается так:
а) (3 + 6) + 7 = 3 + (6 + 7); в) (7 - 3) - 6 = (7 - 6) - 3;
б) (7 - 3) + 6 = 7 + (6 - 3); г) свой ответ .
Свойство вычитания числа из суммы для числа 3 и суммы 2 и 5 записывается так:
а) (2 + 5)-3 = (5-3) + 2 в)(2 + 3) - 5 = (5 - 3) + 2
б) 5 - (3 + 2) = (5 - 2) – 3 г)свой ответ.
*. Чему равна сумма самого большого и самого маленького из чисел, составленных из цифр 2, 4 и 6? (В любом числе каждая цифра используется только один раз)
а) 672; в) 396;
б) 888; г) свой ответ.
Приложение 4
Тест 3
ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Вариант 1
Ответьте на вопросы, выполните задания (подчеркните верный ответ или предложите свой).
Какая из записей является числовым выражением?
а) (18-7) +а; в)х + 10 = 28;
б) 36 : 6 + 7; г) свой ответ.
Найдите значение выражения (у - 312) + 59 при у = 700.
а) 471; в) 437;
б) 447; г) свой ответ.
Женя на рыбалке поймал 17 рыб, а Саша на т рыб больше. Сколько все�го рыб поймали Саша и Женя вместе? Вычислите при т = 8.
а) 26; в) 42;
б) 25; г) свой ответ.
Как с помощью букв записывается переместительное свойство сложения?
а) а + (в + с) = (а + в) + с; в) а + в=в+ а;
б) а-в = в-а г) свой ответ.
Как с помощью букв записывается свойство вычитания суммы из числа?
а) а - (в+ с) = а - в + с; в)a-(b +c) =a-b-c;
б)(а + в)- с= a-в– с; г) свой ответ.
Если разность х - 18 есть натуральное число, то какие значения может принимать х?
а) 18; в) 20;
б) 13; г) свой ответ.
Найдите по формуле пути значение скорости и, еслиt = 6 ч,s= 240 км.
а) 30 км/ч; в) 40 км/ч;
б) 1440 км; г) свой ответ.
8*. Чему равна сумма наибольшего трехзначного числа и трех последу�ющих чисел?
а) 3606; в) 4002;
б) 3990; г) свой ответ.
Вариант 2
Ответьте на вопросы, выполните задания (подчеркните верный ответ или предложите свой).
Какая из записей является буквенным выражением?
а) (18 - 7) + а; в)х+ 10 = 28;
б) 36 : 6 + 7; г) свой ответ.
Найдите значение выражения (у - 312) + 59 при у = 710.
а) 461; в) 457;
б) 447; г) свой ответ.
Мина прополола 13 грядок, а Галяна у грядок меньше. Сколько грядок пропололи Нина и Галя вместе? Вычислите при у = 5.
а) 31; в) 18;
б) 21; г) свой ответ.
Как с помощью букв записывается сочетательное свойство сложения?
а) а + (в + с) = (а + в) + с; в) а + в =в + а;
б) a- в =в-а; г) свой ответ.
Как с помощью букв записывается свойство вычитания числа из суммы?
а) (а + в) - с = а + (в - с); в) (а + в) - с = а - в+ с;
б)a-(b + с)-с = а-в-с; г) свой ответ.
Если разность 18 – х есть натуральное число, то какие значения может принимать x?
а) 18; в) 13;
б) 20; г) свой ответ.
Найдите по формуле пути значение времени, еслиv= 80 км/ч,s= 240 км.
а) 3 ч; в) 19 200 км;
б) 4 ч; г) свой ответ.
8*. Чему равна сумма наименьшего трехзначного числа и трехпредшествующих чисел?
а) 406; в) 394;
б)390; г) свой ответ .
Приложение 5
Тест 4.УРАВНЕНИЕ
Вариант 1
Выберите и подчеркните верное утверждение или предложите свое.
Уравнением называется:
а) числовое выражение, значение которого нужно найти;
б) буквенное выражение, значение которого нужно найти;
в) равенство, содержащее букву, значение которой нужно найти;
г) свой ответ.
Решить уравнение - значит найти:
а) корни или убедиться, что их нет;
б) сумму;
в)корни;
г) свой ответ
Чтобы найти неизвестное уменьшаемое, нужно:
а) к разности прибавить вычитаемое;
б) из разности вычесть вычитаемое;
в) разность умножить на вычитаемое;
г) свой ответ.
Корень уравнениях - 17 = 33 равен:
а) 50; б) 16; в) 40; г) свой ответ.
В уравнении 128 -х = 35 неизвестно:
а) вычитаемое; в) разность;
б) уменьшаемое; г) свой ответ.
Уменьшаемым в уравнении х - 25 = 144 является число:
а) 144;б) хв) 25; г) свой ответ.
Первое слагаемое равно 33, сумма 100, тогда второе слагаемое равно:
а) 133; б) 77; в) 67; г) свой ответ.
8*. Сумма трех слагаемых равна 77 777. Одно слагаемое равно 3 333, вто�рое 444, тогда третье слагаемое равно:
а) 74 000;б) 81 554; в) 100 444; г) свой ответ.
Вариант 2
Выберите и подчеркните верное утверждение или предложите свое.
Равенство, содержащее букву, значение которой нужно найти, называется:
а) буквенным выражением;
б) числовым выражением;
в) уравнением;
г) свой ответ.
Корнем уравнения называется значение буквы, при котором из уравнения получается:
а) верное буквенное равенство;
б) верное числовое равенство;
в) верное выражение;
г) свой ответ.
Чтобы найти неизвестное вычитаемое, нужно:
а) к разности прибавить уменьшаемое;
б) из уменьшаемого вычесть разность;
в) уменьшаемое умножить на разность;
г) свой ответ
Корень уравнения 37 – у = 16 равен:
а) 43; б) 53; в) 21; г) свой ответ.
В уравнении х — 128 = 35 неизвестно:
а) вычитаемое; в) разность;
б) уменьшаемое; г) свой ответ.
Вычитаемым в уравнении 144 - х = 25 является число:
а) 25; б) 169; в) 119;г) свой ответ.
Одно из слагаемых равно 44, сумма 100, тогда второе слагаемое равно:
а) 144; б) 56; в) 66; г) свой ответ.
8*. Сумма трех слагаемых равна 99 999. Одно слагаемое равно 1111, а второе 888, тогда третье слагаемое равно:
а) 101 998; б) 98 000; в) 100 888; г) свой ответ.
Приложение 6
Тест 5
УМНОЖЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ
Вариант 1
Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
Найдите корень уравнения х : 19 = 38.
а) 19; в) 722;
б) 2; г) свой ответ.
Найдите произведение, а • 0.
а) 0; в) а;
б) 1; г) свой ответ.
Найдите произведение чисел 54 651 и 1.
а) 54 652; в) 54 651;
б) 1; г) свой ответ.
Найдите произведение чисел 302 и 507.
а) 17214; в) 809;
б)153114; г) свой ответ.
Найдите произведение чисел 100 и 513.
а) 5130; в) 51300;
б)613; г) свой ответ.
Упростите выражение 7 • с + 11 с.
а) 18 +с; в) 18 • с • с;
б) 18 • с; г) свой ответ.
Раскройте скобки 4 • (а + 11).
а) 4 • а+ 11; в) а+ 44;
б) 4 • а + 44; г) свой ответ.
Скорость теплохода 36 км/ч. На каком расстоянии от пристани он будет через 3 ч?
а) 12 км/ч; в) 108 км/ч;
б) 108 км; г) свой ответ.
9*. Чему равно наибольшее произведение двух различных двузначных чи�сел, составленных из цифр 1, 2, 3 и 4 (должна использоваться каждая цифра и только один раз)?
а) 903; в) 1462;
б) 1312; г) свой ответ.
Вариант 2
Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
Найдите корень уравнения х : 48 = 12.
а) 4; в) 60;
б) 576; г) свой ответ.
Найдите произведениеа • 1.
а) а; в) 1;
б) 0; г) свой ответ.
Найдите произведение чисел 765095 и 0.
а)765095; в)7650950;
б) 0 г) свой ответ.
Найдите произведение чисел 109 и 307.
а) 416; в) 33463;
б) 44363; г) свой ответ.
Найдите произведение чисел 800 и 70.
а) 56; в) 56 000;
б) 15 000; г) свой ответ.
Упростите выражение 12 • х- 4 • х.
а) 8 - х; в) 8 • х •х;
б) 8 • х; г) свой ответ.
Раскройте скобки 3 • (а + 12).
а) 3 • a + 36; в) а + 36;
б) 3 • а + 12; г) свой ответ.
На стройке было 44 машины, а через месяц их стало в 4 раза больше. Сколько машин стало на стройке?
а) 11; в) 48;
б) 176; г) свой ответ.
9*. Чему равно наибольшее произведение двух различных двузначных чи�сел, составленных из цифр 1, 2, 3 и 5 (должна использоваться каждая цифра и только один раз)?
а) 2916; в) 1632;
б) 2142; г) свой ответ.
Приложение 7
Тест 6
ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ
Вариант 1
Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
Найдите частное чисел 7856 и 1.
а) 1; в) 7855;
б) 7856; г) свой ответ .
Найдите корень уравнения а: 15 = 135.
а) 150; в) 9;
б) 2025; г) свой ответ .
Найдите корень уравнения 32832 :х = 108.
а) 304; в) 32940;
б) 34; г) свой ответ .
Найдите второй множитель, если первый равен 13, а произведение равно 1352.
а) 14; в) 104;
б) 1365; г) свой ответ .
Найдите частное чисел 3750 и 30.
а) 125; в) 1250;
б) 3780; г) свой ответ .
Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколь�ко раз скорость велосипедиста больше скорости пешехода?
а) в 100 раз; в) в 4 раза;
б) в 15 раз; г) свой ответ
В одной книге 480 страниц, а в другой в 4 раза меньше. Сколько страниц во второй книге?
а) 12; в) 1920;
б) 120; г) свой ответ .
8*. Найдите два числа, если известно, что одно из них в 18 раз больше дру�гого, а их сумма равна 1083.
а) 85 и 998; в) 57 и 1026;
б) 58 и 1102; г) свой ответ
Вариант 2
Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
Найдите частное чисел 4583 и 1.
а) 1; в) 4583;
б) 4584; г) свой ответ.
Найдите корень уравнения 51706 : х = 103.
а) 5325718; в) 52;
б) 502; г) свой ответ.
Найдите корень уравнения а : 45 = 405.
а) 18225; в) 450;
б) 9; г) свой ответ
Найдите первый множитель, если второй равен 17, а произведение равно 1751.
а) 13; в) 103;
б) 29 767; г) свой ответ.
Найдите частное чисел 7920 и 60.
а) 506; в) 13 365;
б) 132; г) свой ответ.
Скорость лыжника 15 км/ч, а скорость мотоциклиста 45 км/ч. Во сколько раз скорость мотоциклиста больше скорости лыжника?
а) в 3 раза; в) в 2 раза;
б) в 30 раз; г) свой ответ
Сколько времени был в пути теплоход, скорость которого 35 км/ч, а рас�стояние между пристанями 420 км?
а) 120 ч; в) 12 ч;
б) 14700 км/ч; г) свой ответ
8*. Найдите два числа, если известно, что одно из них в 16 раз больше дру�гого, а их разность равна 435.
а) 464 и 29; в) 496 и 31;
б) 458 и 23; г) свой ответ
Приложение 8
ПРОМЕЖУТОЧНАЯ АТТЕСТАЦИОННАЯ КОНТРОЛЬНАЯ РАБОТА
Вариант 1
Вычислите 93 – (83 - 276 :23): 4.
Упростите выражение (8а – 150) — 6а и найдите его значение при а = 1; 12.
Решите уравнение 5х + 7х – 2069 = 5167 .
Выразите в квадратных метрах: 6 га; 5 га;21 а; 18 а.
Решите задачу.
Чтобы приготовить настойку для полоскания рта, надо взять ромашки - 3 части, календулы - 2 части, шалфея - 4 части. Сколько граммов нужно взять шалфея, если ромашки и календулы 100 граммов?
Вариант 2
Вычислите 53- (б3 - 544 :34): 25 .
Упростите выражение 18х - (35 + 7х) и найдите его значение при х = 6; 15.
Решите уравнение 17х – 11х+ 5858 = 8912.
Выразите в гектарах: 630000 м2; 83000 а; 67 км2; 14 га.
Решите задачу.
Для приготовления жидкости для выведения пятен берут воды - 10 частей, нашатырного спирта - 3 части, соли - 2 части. Сколько будет весить вся жид�кость, если воды и спирта в ней будет 26 граммов?
Приложение 9
Тест 7
Обыкновенные дроби
Вариант 1
Выберите и подчеркните верный или предложите свой.
.Числа 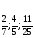 называются: называются:
а) натуральными числами; в) десятичными дробями;
б) обыкновенными дробями; г) свой ответ.
|
 Скачать 2.27 Mb.
Скачать 2.27 Mb. г) свой ответ
г) свой ответ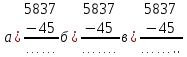 г)свой ответ
г)свой ответ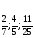 называются:
называются: