«Великий математик России Николай Иванович Лобачевский»
 Скачать 140.2 Kb. Скачать 140.2 Kb.
|
| Муниципальное бюджетное образовательное учреждение Уршельская средняя общеобразовательная школа Исследовательская работе по теме: «Великий математик России Николай Иванович Лобачевский» Научный руководитель: Зубенко Н.А. учитель математики Работу выполнила: Гусарова Алла ученица 10 класса 2012 год Оглавление. Введение………………………………………………….3 Основная часть I.Биография……………………………………………………4 II. Студенческие годы………………………………………..5 III. Геометрия Лобачевского………………………………..6 IV. Другие достижения Лобачевского……………………8 V.Последние годы жизни. Заключение I.Вклад Лобачевского в разные сферы науки…………….11 Библиографический список……………………………..12 I.Используемая литература. II.Web ресурсы Приложение. I. Награды и звания Лобачевского………………………...13 II. Память………………………………………………………15 Введение. В этом году исполняется знаменательная дата со дня рождения великого математика Николая Ивановича Лобачевского, внесшего огромнейший вклад в развитие различных областей науки. На уроках геометрии я услышала о том, какой переворот осуществила его теория в классической геометрии Евклида. Ведь в течение двух тысяч лет геометрию узнавали либо из «Начал» Евклида, либо из учебников, написанных на основе этой книги. Мне захотелось узнать как можно больше об этом человеке, как о личности. Именно поэтому я занялась изучением его биографии. Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки. Я заинтересовалась фактом, что через точку можно провести более одной прямой, параллельной данной. Прочитав статьи о его биографии, я стала изучать его вклад в различные области науки. Меня очень поразило то, насколько широка была область его достижений. Ведь его вклад был не только в геометрии, алгебре, математическом анализе, но и значительны заслуги в области теории вероятности, физики, механики, астрономии. В своей работе я представила обзор труда Лобачевского Н.И. в различных областях науки. Цель работы – попытаться показать и раскрыть часть творчества выдающегося математика Лобачевского Н.И., кратко рассмотреть основные положения наиболее известных его теорий, которые широко используются в настоящее время не только в образовании, но и нашли применение в области высоких точных технологий, инженерного проектирования в различных областях промышленного производства. Основная часть.
 Рисунок 1. Никола́й Ива́нович Лобаче́вский. Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792— 12 (24) февраля 1856) — русский математик, деятель университетского образования и народного просвещения, создатель неевклидовой геометрии Н. И. Лобачевский родился в Нижнем Новгороде. Его родителями были Иван Максимович Лобачевский (чиновник в геодезическом департаменте, годы жизни: 1760—1800) и Прасковья Александровна Лобачевская; Николай был средним из их троих сыновей. Отец Николая Ивановича тяжело заболел и умер в возрасте всего 40 лет, оставив детей и жену Прасковью Александровну в трудном материальном положении. В 1802 году Прасковья Александровна отдала всех троих сыновей в Казанскую гимназию.Николай Лобачевский окончил гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам — латинскому, немецкому, французскому. В проявившемся уже тогда его интересе к математике — большая заслуга преподавателя гимназии Г. И. Карташевского. II. Студенческие годы. Еще будучи студентом первого курса, молодой Лобачевский обратил на себя внимание профессора Бартельса, который взялся лично руководить обучением необыкновенно способного студента. Это Лобачевскому было очень необходимо, так как своим вольнодумством и многочисленными шалостями он часто вызывал неудовольствие университетских властей. . На старшем курсе в характеристику Лобачевского включили «мечтательное о себе самомнение, упорство, неповиновение», а также «возмутительные поступки» и даже «признаки безбожия». Над ним нависла угроза отчисления, но заступничество Бартельса и других преподавателей помогло отвести опасность. Мнение Бартельса о том, что «…Лобачевский, как студент, отличается такими способностями и имеет такие достижения, что в любом из германских университетов он был бы признан выдающимся студентом…», представленное Сенату университета, предотвратило исключение будущего ученого из университета. Лобачевский закончил университет в 1811 году и остался в нем в качестве ассистента Бартельса. Спустя три года он был назначен адъюнктом. Он хотел в это время издать свою первую работу под заглавием «Геометрия», однако работа пролежала а архиве больше семидесяти лет, потому что никто из членов Академии не мог ее понять. В 1816 году Лобачевскому присвоили звание профессора. В Казанском университете Лобачевский, наряду с математическими дисциплинами, читал лекции по астрономии, расширяя и углубляя их содержание. Его лекции, например, были посвящены определению элементов орбит, их вековым изменениям, теории приливов и отливов, теории возмущенного движения комет и спутников планет. Проводил в 1811-42 астрономические наблюдения, в частности наблюдал комету 1811 и комету Энке в 1832, но дневники его наблюдений сгорели во время пожара обсерватории Казанского университета. III. Геометрия Лобачевского. Первым человеком, отважившимся выступить с совершенно новой, отличной от Евклидовой, теорией геометрии, был Николай Иванович Лобачевский. Открытие Лобачевского (1826, опубликованное 1829-30), не получившее признания современников, совершило переворот в представлении о природе пространства, в основе которого более 2 тыс. лет лежало учение Евклида, и оказало огромное влияние на развитие математического мышления. Тем самым он положил начало новой эпохе в этом разделе математики, завоевав себе почетное звание „Коперника геометрии". Так его назвал известный английский математик Уильям Клиффорд. Сохранились студенческие записи лекций Лобачевского (от 1817), где им делалась попытка доказать пятый постулат Евклида, но в рукописи учебника «Геометрия» (1823) он уже отказался от этой попытки. В «Обозрениях преподавания чистой математики» за 1822/23 и 1824/25 Лобачевский указал на «до сих пор непобедимую» трудность проблемы параллелизма и на необходимость принимать в геометрии в качестве исходных понятия, непосредственно приобретаемые из природы. 7 февраля 1826 Лобачевский представил для напечатания в Записках физико-математического отделения сочинение: «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных» (на французском языке). Но издание не осуществилось. Рукопись и отзывы не сохранились, однако само сочинение было включено Лобачевским в его труд «О началах геометрии» (1829—1830), напечатанный в журнале «Казанский вестник». Это сочинение стало первой в мировой литературе серьёзной публикацией по неевклидовой геометрии, или геометрии Лобачевского. На протяжении 1829—1840 годов Николай Иванович Лобачевский опубликовал несколько работ, в частности, “ Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных” . В этой работе он принял знаменитую аксиому, противоречащую аксиоме Евклида, а именно: через данную точку, лежащую на одной и той же плоскости, что и данная прямая, можно провести бесконечное количество прямых, параллельных данной. 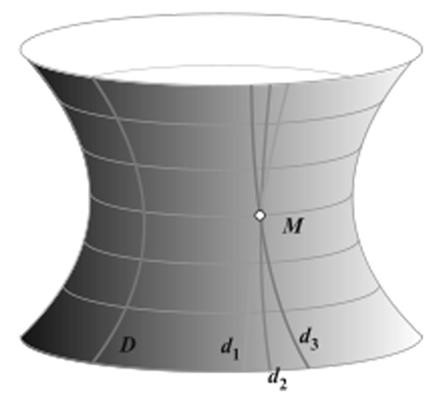 Рисунок 2. Наглядное представление геометрии Лобачевского через точку M проходят две прямые, параллельные прямой D. Аксиома же Евклида гласит, что через такую точку можно провести только одну параллельную прямую. Разработанная Лобачевским новая геометрия не включает в себя евклидову геометрию, однако евклидова геометрия может быть из нее получена предельным переходом (при стремлении кривизны пространства к нулю). Геометрия Лобачевского представляет собой величайшее открытие в математике. Он доказал, что могут существовать различные теории геометрии, отличные от Евклидовой и не противоречащие друг другу. Однако, современные Лобачевскому ученые не обратили внимания на эту выдающуюся работу. Наоборот, Лобачевский встретился с колкостями со стороны лиц, не понимающих новой математической теории. Не обескураженный неудачей Лобачевский начал борьбу за триумф своих идей и в ряде работ многократно и по-разному обосновал неевклидову геометрию, и показал пример использования ее в интегральном исчислении. И все же его идея нашла полное признание и применение как в математике, так и в физике только лишь через много лет после его смерти. В физике, например, закон суммирования скоростей в теории относительности основан на методе суммирования отрезков, предложенном Лобачевским. Не найдя понимания на родине, математик пытается найти единомышленников за рубежом. В 1840 г. Лобачевский печатает на немецком языке «Геометрические исследования по теории параллельных», где содержится чёткое изложение его основных идей. Один экземпляр получает Гаусс, «король математиков» той поры. Как много позже выяснилось, Гаусс и сам тайком развивал неевклидову геометрию, однако так и не решился опубликовать что-либо на эту тему. Ознакомившись с результатами Лобачевского, он выразил свою симпатию к идеям русского учёного косвенно: рекомендовал избрать Лобачевского иностранным членом-корреспондентом Гёттингенского королевского общества. Восторженные отзывы о Лобачевском Гаусс доверил только своим дневникам и самым близким друзьям. Это избрание состоялось в 1842 году. Однако положения Лобачевского оно не укрепило. Ему осталось работать в родном университете ещё четыре года. IV. Другие достижения Лобачевского. Лобачевский был не только геометром исключительной творческой силы, но и математиком с широким диапазоном научной работы. Ему принадлежит ряд фундаментальных работ в области алгебры («Алгебра или вычисление конечных», 1834, и др.) и математического анализа («Об исчезновении тригонометрических строк», 1834, «О сходимости бесконечных рядов», 1841, «О значении некоторых определённых интегралов», 1852, и др.). В области анализа Лобачевский получил новые результаты в теории тригонометрических рядов. Им же установлен один из наиболее удобных методов приближённого решения уравнений (метод Лобачевского). Лобачевский всю свою жизнь трудился над разработкой своей теории геометрии, но занимался и другими разделами математики. В частности, он разработал метод приблизительного решения алгебраических уравнений и его порядка: Лобачевского метод, метод приближённого (численного) решения алгебраических уравнений состоит в построении уравнения f1(x) = 0, корни которого являются квадратами корней исходного уравнения f(x) = 0. Затем строят уравнение f2(x) = 0, корнями которого являются квадраты корней уравнения f1(x) = 0. Повторяя этот процесс несколько раз, получают уравнение, корни которого сильно разделены. В случае если все корни исходного уравнения действительны и различны по абсолютной величине, имеются простые вычислительные схемы Л. м. для нахождения приближённых значений корней. В случае равных по абсолютной величине корней, а также комплексных корней вычислительные схемы метода Лобачевского очень сложны. Лобачевский получил ряд ценных результатов и в других разделах математики: так ,в математическом анализе получил ряд тонких теорем о тригонометрических рядах, уточнил понятие непрерывной функции : …Общее понятие функции требует, чтобы функцией от «называть число», которое даётся для каждого и вместе с постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной… Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе. Занимался Лобачевский также и теорией вероятностей. В разные годы он опубликовал несколько содержательных статей по алгебре, теории вероятностей, механике, физике, астрономии и проблемам образования. Также он вместе со своим учеником М.В.Ляпуновым участвовал в экспедиции в Пензу для наблюдения полного солнечного затмения 8 июля 1842. Подробно описал свои наблюдения и размышления по поводу загадочных в то время явлений протуберанцев и солнечной короны. Занимался также усовершенствованием методов обработки астрономических наблюдений. Будучи ректором Казанского университета, способствовал развитию астрономии в Казани. По его инициативе при университете в 1833-37 годах была построена новая обсерватория, одна из лучших по тому времени. Она начала работать в 1838, на год раньше Пулковской. Не занимаясь астрономией непосредственно, Лобачевский, создав новую геометрию, пришел к выводам, имеющим огромное значение и для астрономии. Геометрия Лобачевского нашла применение в общей теории относительности. Если считать распределение вещества во Вселенной равномерным (что в космических масштабах допустимо), то при определенных условиях пространство будет иметь геометрию Лобачевского. Таким образом, в современной космологии оправдалось предположение Лобачевского о неевклидовой геометрии реального пространства. V.Последние годы жизни. Лобачевский потерял зрение и свою последнюю работу Пангеометрия" диктовал. Николай Иванович Лобачевский умер в 1856 году в Казане с верой в то, что его работа будет понята и продолжена учеными будущих поколений. Лобачевский умер непризнанным. Спустя несколько десятилетий ситуация в науке коренным образом изменилась. Большую роль в признании трудов Лобачевского сыграли исследования Э. Бельтрами (1868), Ф. Клейна (1871), А. Пуанкаре (1883) и др. Появление модели Клейна доказало, что геометрия Лобачевского так же непротиворечива, как и евклидова. Заключение. I.Вклад Лобачевского в разные сферы науки. Открытие Лобачевского поставило перед наукой по крайней мере два принципиально важных вопроса, не поднимавшихся со времен "Начал" Евклида: "Что такое геометрия вообще? Какая геометрия описывает геометрию реального мира?". До появления геометрии Лобаческого существовала только одна геометрия - евклидова, и, соответственно, только она могла рассматриваться как описание геометрии реального мира. Ответы на оба вопроса дало последующее развитие науки. Лобачевский вошел в историю математики не только как гениальный геометр, но и как автор фундаментальных работ в области алгебры, теории бесконечных рядов и приближенного решения уравнений. Создание и разработка геометрии Лобачевского поставили вопрос об исследовании всей структуры системы аксиом, как евклидовой геометрии, так и других возникающих к этому времени геометрий и выяснение независимости этих аксиом друг от друга. Выдающийся вклад Николая Лобачевского в различные математические области были признаны как на родине гения, так и за рубежом. Библиографический список. Литература Лаптев Б.Л. Николай Иванович Лобачевский. 1792 - 1856. - В сб.: Люди русской науки. Web ресурсы https://znamus.ru/page/Nikolaj_Lobachevskij https://bestreferat.ru/referat-207255.html https://1matematiki.ru/nikolaj-ivanovich-lobachevskij/ https://sonkol.ru/main/494.html https://russer.ru/a/a/lobachevskiy_nikolay_ivanovich_-_drugie_nauchnyie_dostijeniya https://ru.wikipedia.org/wiki/Лобачевский,_Николай_Иванович#.D0.91.D0.B8.D0.BE.D0.B3.D1.80.D0.B0.D1.84.D0.B8.D1.8F https://piplz.ru/page-id-136.html https://math.ru/history/people/Lobachevskii Приложение. I. Награды и звания Лобачевского. В течение жизни Н. И. Лобачевский получил за неутомимую и плодотворную служебную деятельность несколько наград:
Таблица 1. Награды и звания. II. Память. В России в 1892 году широко отметили 100-летний юбилей Лобачевского. Была учреждена международная премия (Медаль Лобачевского, 1895), в Казани открыт памятник учёному (1896). 20 марта 1956 г. вышел указ президиума Верховного Совета СССР о присвоении Горьковскому (Нижегородскому) университету имени Н. И. Лобачевского. 200-летие Лобачевского отмечалось в 1992 году. Банком России была выпущена памятная монета в серии «Выдающиеся личности России». В русской научной и научно-популярной литературе, как и в литературе многих других стран, имеется немало сочинений, посвященных неевклидовой геометрии Лобачевского. В честь Лобачевского названы: Малая планета № 1858. Кратер на обратной стороне Луны (9.9°N, 112,6°E). Научная библиотека Казанского университета. Улицы в Москве, Киеве, Казани, Липецке и др. городах. Один из самолётов Аэрофлота. Школа № 52 во Львове, Украина. Лицей им. Н. И. Лобачевского при КГУ (Казань). 20 марта 1956 года вышел указ Президиума Верховного Совета СССР о присвоении Горьковскому (Нижегородскому) университету имени Н. И. Лобачевского. Казанский университет, который намного больше заслуживал этой чести, не получил имя Лобачевского, потому что в 1925 году ему было присвоено имя В. И. Ульянова-Ленина (Ленин учился там в 1887 году). |



