|
«Рациональные уравнения»
Шубина Татьяна Викторовна
Учитель математики МБОУ «СОШ № 24» г.Рубцовска, Алтайского края
8 класс
Тема урока «Рациональные уравнения»
Предмет : алгебра
Класс, характеристика класса: 8 класс; общеобразовательный класс.
Этот урок проводится в классе, где большинство учащихся имеют хорошие прочные знания, умения и навыки, их отличают высокий уровень воспитанности, коммуникативности, мотивации учения. Класс в целом способен очень хорошо работать на уроках, может решать достаточно сложные познавательные задачи. В то же время «расшевелить» класс, побудить учащихся к активной деятельности бывает нелегко.
Тема урока: « Рациональные уравнения»
Номер урока в системе изучаемой темы: на предыдущих уроках изучили формулы решения корней квадратного уравнения
Образовательные результаты, на достижение которых направлено содержание урока.
Цель: Изучить способы решения биквадратных уравнений. В результате чего ученик должен:
- знать, какое уравнение называется биквадратным;
- знать, как вводить новую переменную в биквадратном уравнении;
- составить алгоритм решения биквадратного уравнения;
- уметь планировать процесс решения и видеть его результат;
- развивать критическое мышление: выделять ошибки в рассуждениях;
- уметь ясно и точно излагать свои мысли.
Тип урока: урок введения новых знаний и формирования первичных умений.
Используемое оборудовании: компьютер, проектор, доска, мел.
Описание технологической карты урока
Этап урока
|
Задачи
|
Время урока
|
Показатели выполнения задач
(образовательный продукт, описание критериев достижения целей и задач данного этапа урока)
|
учителя
|
учащихся
|
1 мин.
|
Доброжелательный настрой учителя и учащихся, кратковременность этапа, быстрое включение класса в работу, организация внимания учащихся.
|
Организационный
|
Обеспечить нормальную обстановку для работы, психологически подготовить учащихся к предстоящему уроку
|
Подготовиться к уроку, морально настроиться к предстоящей учебной деятельности
|
Подготовительный
|
Организовать и целенаправить познавательную деятельность учащихся; подготовить к усвоению нового материала, создание проблемной ситуации
|
вспомнить формулы решения квадратного уравнения, что такое степень уравнения, как представить выражение в виде квадрата некоторой степени; сформулировать проблему; поставить перед собой учебную задачу
|
12 мин.
|
Успешное выполнение учащимися заданий, в которых требуется представить выражение в виде квадрата некоторой степени, определить степень уравнение и нахождение корней квадратного уравнения; выявление проблемной ситуации
|
Введение новых знаний
|
Ввести понятие биквадратного уравнения; Организовать деятельности учащихся по составлению алгоритма решения биквадратного уравнения в группах; создать условия для презентации групповой работы и выбора верного алгоритма
|
Разработать в группах алгоритм решения биквадратного уравнения, презентовать продукт своей работы перед классом и доказать его правильность; выбрать верный алгоритм из предложенных
|
12 мин
|
Составление учащимися единого алгоритма решения биквадратного уравнения
|
Формирование первичных умений
|
Организовать отработку учащимися алгоритма решения биквадратного уравнения при решении номеров из учебника
|
Учиться применять полученный алгоритм при решении уравнений
|
11 мин
|
Успешное решение учащимися биквадратных уравнений по разработанному алгоритму
|
Информация о домашнем задании
|
Сообщить учащимся домашнее задание
|
Записать информацию о домашнем задании в дневник
|
1 мин
|
Наличие записи о домашнем задании в дневниках у учащихся
|
Заключительный этап
|
Организовать работу по подведению итога урока
|
Систематизировать полученные на уроке знания
|
3 мин
|
Учащиеся владеют понятием биквадратного уравнения. Умение учащимися применять алгоритм при решении биквадратных уравнений.
|
Описание процессуальной части урока
Этапы урока
|
Деятельность
|
учителя
|
учащихся
|
|
Приветствие учащихся, отметка отсутствующих в классе в журнале с помощью дежурных, мобилизация внимания.
- Наш сегодняшний урок я хотела бы начать со слов Л.Н.Толстого:
«Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».
Слайд 1
|
Приветствие учителя
|
2
|
– Ребята, с каким видом уравнений вы познакомились на предыдущих уроках.
– Сегодня на уроке мы продолжаем изучать рациональные уравнения и познакомимся с новым видом рационального уравнения, приводимого к квадратному.
– Откройте тетради, запишите число и тему урока «Рациональные уравнения».
Слайд 1
Фронтальный опрос. Слайд 2
– Квадратным уравнением называется уравнение вида ______________, где
Слайд 3
– От чего зависит количество корней квадратного уравнения?
– Как обозначается дискриминант и по какой формуле вычисляется?
– По какой формуле вычисляются корни квадратного уравнения?
Слайд 4
– Сколько решений может иметь квадратное уравнение?
Если D < 0, то уравнение…….
Если D > 0, то уравнение…….
Если D = 0, то уравнение…….
Слайд 5
– Посмотрите на экран и выполните следующие задания в тетрадях. Слайд 6
1.Представьте выражение в виде квадрата:
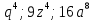
2.Определите степень уравнения и вычислите его корни:
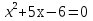
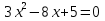
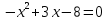
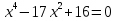
– Итак, давайте проверим результаты вашей работы.
– Действительно, последнее уравнение – это уравнение четвертой степени. Уравнения такого вида называются биквадратными.
Уравнение вида ах4 + bх2 +с = 0 называют биквадратным уравнением.
“БИ” - дважды, биквадратное - дважды квадратные.
Сегодня на уроке мы будем с вами учиться решать такие уравнения.
– Посмотрите внимательно на старший член этого уравнения и представьте его в виде квадрата некоторого выражения.
– Какой вид тогда примет данное уравнение?
– Относительно какого выражения биквадратное уравнение является квадратным?
|
– На предыдущих уроках мы изучали рациональные уравнения.
Записывают число и тему урока в тетрадях.
– Квадратным уравнением называется уравнение вида ах2 + bх +с = 0, где х – неизвестное число, а, b, с – данные числа, причем а ≠ 0.
Числа, а, b, с – коэффициенты квадратного уравнения. Число а называется первым коэффициентом, b – вторым коэффициентом, с – свободным членом.
– От значения дискриминанта.
– Дискриминант вычисляется по формуле D=b2 – 4аc
– Корни квадратного уравнения вычисляются по формуле:
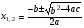
– Если D < 0, то уравнение не имеет действительных корней.
Если D > 0, то уравнение имеет 2-а различных действительных корня.
Если D = 0, то уравнение имеет один (двукратный) действительный корень.
Выполняют задания в тетради.
1.
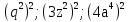
2.Проверяют второе задание, называя его степень и корни.
1 уравнение: уравнение второй степени (квадратное), корни:1 и -6;
2 уравнение: квадратное, корни: не имеет корней;
3 уравнение: уравнение четвертой степени, такие уравнения решать еще не умеем.
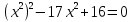
– относительно квадратного
|
3.
|
– Верно. Сейчас я предлагаю вам объединиться в группы по четыре человека и разработать алгоритм решения биквадратного уравнения. На эту работу вам отводится время 5 минут. Затем каждая группа представит разработанный ею алгоритм.
– Сейчас представитель от каждой группы выйдет к доске и запишет свой алгоритм решения биквадратного уравнения.
Учитель координирует процесс обсуждения и разработки совместного алгоритма, направляет деятельность учащихся в правильное направление.
– Решим наше уравнение по данному алгоритму. Кто сможет решить сам биквадратное уравнение по этому алгоритму?
– Обратите внимание на форму записи решения на доске биквадратного уравнения.
– Есть ли затруднения при его решении?
– Метод решения, который мы рассмотрели называется методом введения новой переменной.
|
– Объединяются в группы по 4 человека по принципу 2-х соседних парт и разрабатывают алгоритм.
– Каждая группа предлагает свой алгоритм. И решает уравнение
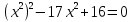
по своему алгоритму.
По итогам обсуждения вырабатывается учащимися совместно с учителем следующий алгоритм:
Алгоритм решения биквадратного уравнения. Метод введения новой переменной. Слайд (7)
1. Ввести замену переменной: пусть х2 = t, t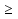 0. 0.
2. Составить квадратное уравнение с новой переменной: аt2 + bt + с = 0 (1).
3. Решить новое квадратное уравнение (1).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного уравнения.
7. Записать ответ.
Евдокимова Алина решает уравнение у доски, остальные – в тетрадях.
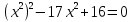
Введем новую переменную
пусть у = х2
Получим квадратное уравнение с
переменной у:
у2– 17у + 16= 0
D = (– 17)2 – 4 ∙ 16 = 225
D > 0, уравнение имеет 2-а различных действительных корня.
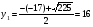 ; ; 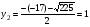
Вернемся к замене переменной.
х2 = 16 или х2 = 1
х = 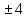 х = ± 1 х = ± 1
Ответ: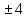 ; ± 1 ; ± 1
– Нет.
|
4.
|
Самостоятельно решают № 868 (б, в, г).
Во время самостоятельной работы учитель помогает в случае необходимости учащемуся индивидуально, контролирует ход работы, оценивает отдельных учащихся за работу на уроке.
|
Ученики работают самостоятельно над решением биквадратных уравнений. Результаты работы постепенно появляются на доске.
|
5.
|
Целью домашнего задания является выполнение заданий на репродуктивном уровне (для этого прошу прочитать §21 п.2. стр. 132, 133, решить №869 а,b). Чтобы соответствовать частично поисковому уровню, надо объяснить от чего зависит число решений биквадратного уравнения.
Слайд 8
|
Записывают домашнее задание в дневники.
|
6.
|
– Итак, подведем итоги урока и наметим перспективы деятельности на следующем уроке.
Фронтальный опрос:
– Какие понятия мы сегодня повторили?
– С каким новым видом уравнений вы сегодня познакомились?
– Какой метод решения биквадратного уравнения вы применяли?
– Могут ли рациональные уравнения служить математическими моделями реальных ситуаций?
– Благодарю всех за работу. Вы молодцы. До свидания
|
Определение квадратного уравнения, дискриминант квадратного уравнения, формулу корней квадратного уравнения.
– Биквадратным уравнением.
– Метод введения новой переменной.
– Наверное, да. Но этот вопрос надо дополнительно изучать.
– До свидания.
|
Приложение: Используемые методы и приемы
Эвристический, репродуктивный методы: Эвристическая беседа с учащимися. Актуализация ранее изученных знаний, которые будут востребованы на данном уроке Совместный анализ рассуждений учеников, подвести учеников к. необходимости изучения способа решения биквадратных уравнений. Создание проблемной ситуации.
Список используемой литературы.
Владимирцева С.А. Теория и методика обучения математике: Общая методика: Учебное пособие.– Барнаул: Изд-во БГПУ, 2005. – 158 с.
Терновая Г.В. Теоретические основы и практика проектирования современного урока.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.2: Задачник для общеобразоват. учреждений. – 7-е изд. – М.: Мнемозина, 2005. – 239с.: ил.
|
|
|
 Скачать 105.29 Kb.
Скачать 105.29 Kb.
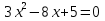
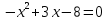
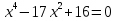
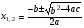
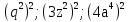
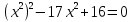
 0.
0.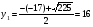 ;
; 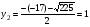
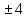 х = ± 1
х = ± 1