Тригонометрическая форма записи комплексного числа
 Скачать 34.99 Kb. Скачать 34.99 Kb.
|
| Тригонометрическая форма записи комплексного числа. Геометрическую интерпретацию комплексного числа впервые дал Карл Гаусс (1832 г.) После этого комплексные числа вошли в математику наравне с действительными и другими числами. Пусть дано произвольное комплексное число 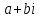 , где a и b – действительные числа, т.е. любое комплексное число однозначно определяется парой действительных чисел. , где a и b – действительные числа, т.е. любое комплексное число однозначно определяется парой действительных чисел.Таким образом, комплексное число можно записать в виде пары чисел: 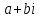 - (a, b) - (a, b) - (b, a) - (b, a)x y a b 0 φ (a, b) r Это означает, что любому комплексное число мы можем однозначно представить точкой на плоскости, которую будем называть комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Иначе эту точку мы можем задать радиус-вектором, проведенным из начала координат в эту точку, который в свою очередь однозначно определяется своей длиной и углом между радиус-вектором и положительным направлением действительной оси. Определение. Модулем комплексного числа называется длина радиус-вектора, проведенного из начала координат в точку, соответствующую данному комплексному числу на плоскости. Для любого комплексного числа модуль определен однозначно. Определение. Аргументом комплексного числа называется величина угла между радиус-вектором, изображающим данное комплексное число, и положительным направлением действительной оси, при этом: величина берется положительная, если направление отсчета против часовой стрелки, и отрицательная – если по часовой стрелке. Замечание. Единственное число, для которого аргумент не определен – это нулевое число. Аргумент комплексного числа определен неоднозначно с точностью до 2πk. Определение. Два комплексных числа, изображаемых точкой на плоскости, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на 2πk. Исходя из полученного на рисунке прямоугольного прямоугольника 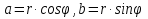 , получаем: , получаем: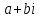 = =Определение. Запись комплексного числа в виде называется тригонометрической формой записи комплексного числа. Задания для работы в классе: Богомолов Практические задания по математике Стр. , № 36, 37 (нечетные цифры) Домашнее задание. Стр. , № 36, 37 (четные цифры) Тригонометрическая форма записи комплексного числа. Геометрическую интерпретацию комплексного числа впервые дал Карл Гаусс (1832 г.) После этого комплексные числа вошли в математику наравне с действительными и другими числами. Пусть дано произвольное комплексное число 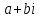 , где a и b – действительные числа, т.е. любое комплексное число однозначно определяется парой действительных чисел. , где a и b – действительные числа, т.е. любое комплексное число однозначно определяется парой действительных чисел.Таким образом, комплексное число можно записать в виде пары чисел: 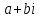 - (a, b) - (a, b) - (b, a) - (b, a)x y a b 0 φ (a, b) r Это означает, что любому комплексное число мы можем однозначно представить точкой на плоскости, которую будем называть комплексной плоскостью. Ось ОХ называется действительной осью, ось ОУ – мнимой осью. Иначе эту точку мы можем задать радиус-вектором, проведенным из начала координат в эту точку, который в свою очередь однозначно определяется своей длиной и углом между радиус-вектором и положительным направлением действительной оси. Определение. Модулем комплексного числа называется длина радиус-вектора, проведенного из начала координат в точку, соответствующую данному комплексному числу на плоскости. Для любого комплексного числа модуль определен однозначно. Определение. Аргументом комплексного числа называется величина угла между радиус-вектором, изображающим данное комплексное число, и положительным направлением действительной оси, при этом: величина берется положительная, если направление отсчета против часовой стрелки, и отрицательная – если по часовой стрелке. Замечание. Единственное число, для которого аргумент не определен – это нулевое число. Аргумент комплексного числа определен неоднозначно с точностью до 2πk. Определение. Два комплексных числа, изображаемых точкой на плоскости, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на 2πk. Исходя из полученного на рисунке прямоугольного прямоугольника 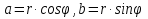 , получаем: , получаем: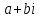 = =Определение. Запись комплексного числа в виде называется тригонометрической формой записи комплексного числа. Задания для работы в классе: Богомолов Практические задания по математике Стр. , № 36, 37 (нечетные цифры) Домашнее задание. Стр. , № 36, 37 (четные цифры) |