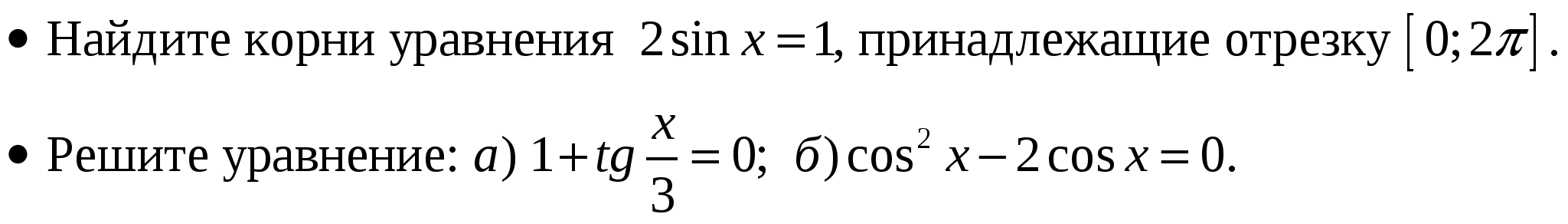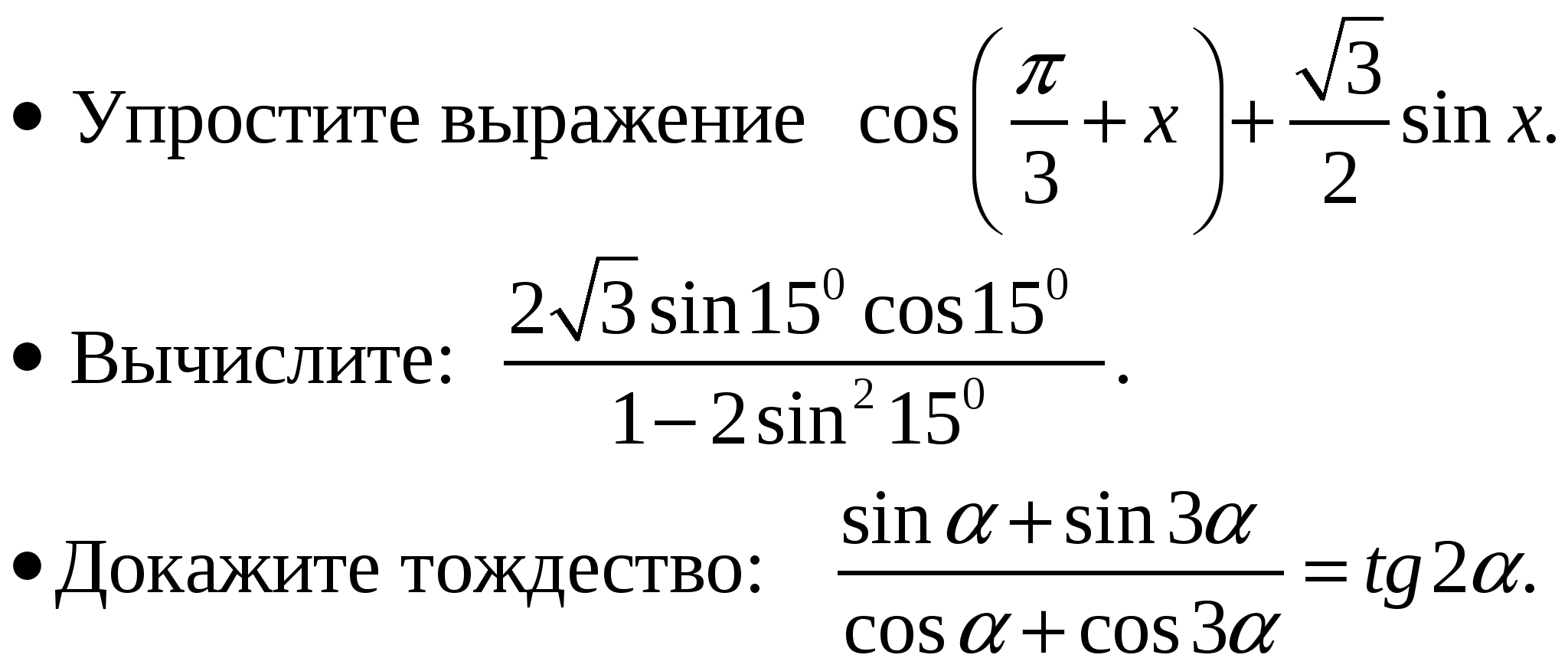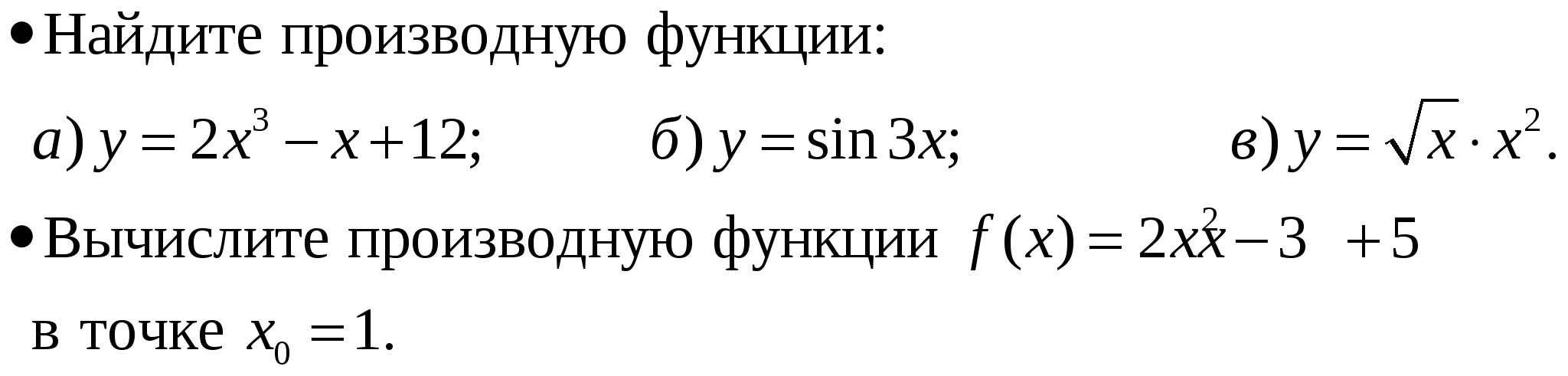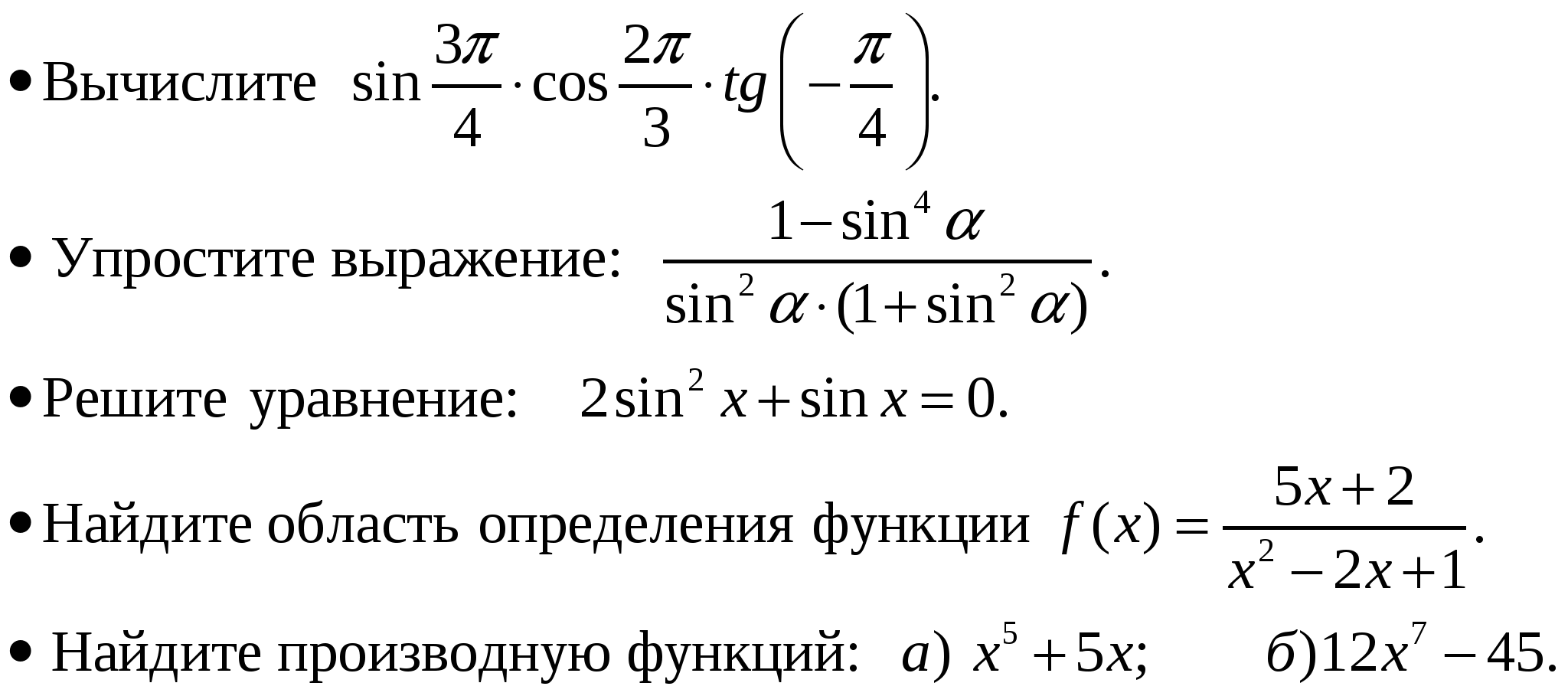|
Уроков математики Кол-во часов за год: Всего 180 часа; в неделю 5 часов
Календарно-тематическое планирование
уроков математики
Кол-во часов за год:
Всего - 180 часа;
В неделю - 5 часов
Плановых контрольных работ: 12 .
Самостоятельных и практических работ: 15
Административных контрольных работ - 3
Планирование составлено на основе программы для общеобразовательных учреждений: Математика. 5-11 кл./ Сост. Г.М.Кузнецова, Н.Г.Миндюк. – М.: Дрофа, 2004, рекомендованная Департаментом образовательных программ и стандартов общего образования МО РФ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса
В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
Программы составлены на основе Государственного стандарта среднего (полного) общего образования по математике. Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ: двухуровневая – уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5»; большой список заданий разного уровня, из которого учащийся решает их по своему выбору. Рядом с учеником на таких уроках – включенный компьютер, который он использует по своему усмотрению.
Урок-контрольная работа. Проводится на трех уровнях:
А – базовый уровень, В – повышенный уровень и С – высокий уровень.
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Разделы математики. Сквозная линия
Функции.
Уравнения и неравенства.
Вычисления и преобразования
Числа и вычисления.
Вычисления и преобразования.
Уравнения и неравенства.
Функции.
Обязательный минимум содержания образовательной области математика
Радианная мера угла. Поворот точки вокруг начала координат.
Определение синуса, косинуса и тангенса угла.
Знаки синуса, косинуса и тангенса углов.
Основные тригонометрические формулы.
Тригонометрические тождества.
Тригонометрические функции.
Тригонометрические уравнения sinx=a, cosx=a, tgx=a, сtgx=a.
Решение тригонометрических уравнений.
Простейшие тригонометрические неравенства.
Синус, косинус, тангенс и котангенс суммы и разности аргументов.
Синус, косинус, тангенс и котангенс двойного угла.
Сумма и разность синусов, косинусов, тангенсов и котангенсов.
Преобразования простейших тригонометрических выражений.
Понятие о пределе и непрерывности функции.
Понятие производной.
Производная степенной функции.
Производная суммы, произведения и частного двух функций.
Производные тригонометрических функций.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц.
Выполнять тождественные преобразования тригонометрических выражений с помощью справочного материала
Знать свойства тригонометрических функций 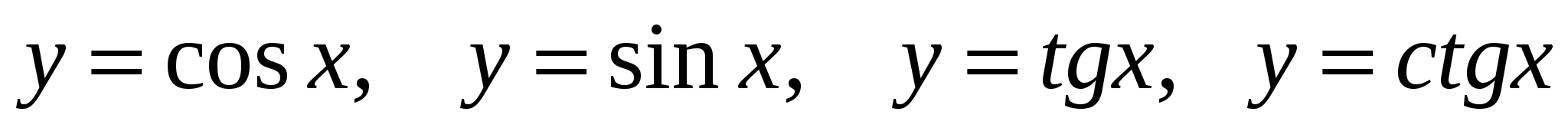 и уметь строить их графики. и уметь строить их графики.
Уметь решать простейшие тригонометрические уравнения.
Выполнять тождественные преобразования тригонометрических выражений с помощью справочного материала.
Уметь находить значения тригонометрических выражений; пользоваться оценкой и прикидкой при практических расчетах.
Уметь вычислять производные элементарных функций, используя справочные материалы.
Уметь исследовать в простейших случаях функции на монотонность.
Уметь находить наибольшие и наименьшие значения функций.
Основные тригонометрические формулы.
Тригонометрические функции
Основные свойства функций.
Решение тригонометрических уравнений.
Простейшие тригонометрические неравенства.
Понятие производной.
Производная степенной функции.
Правила дифференцирования.
Производные тригонометрических функций.
Понятие о пределе и непрерывности функции.
Механический и геометрический смысл производной.
Исследование функций, построение их графикой с помощью производной.
Уметь производить вычисления с действительными числами.
Уметь выполнять тождественные преобразования тригонометрических выражений с помощью справочного материала
Уметь решать несложные алгебраические, тригонометрические уравнения, неравенства.
Знать основные свойства функций и уметь строить их графики.
Уметь находить производные функций, пользуясь правилами дифференцирования .
Понимать механический и геометрический смысл производной.
Применять производные для исследования функций и построения их графиков в несложных случаях.
Уровень возможной подготовки обучающегося
Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. Выполнять тождественные преобразования тригонометрических выражений.
Уметь применять тригонометрические формулы в при решении практических задач
Знать свойства тригонометрических функций 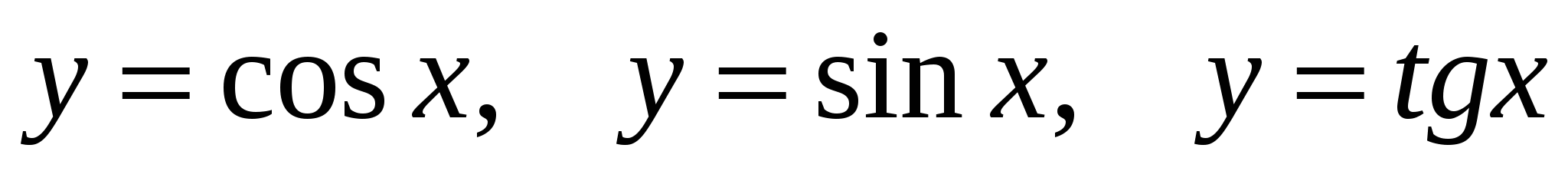 и уметь строить их графики. Уметь выполнять преобразования графиков. и уметь строить их графики. Уметь выполнять преобразования графиков.
Уметь решать тригонометрические уравнения.
Овладеть некоторыми приемами решения тригонометрических уравнений.
Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. Выполнять тождественные преобразования тригонометрических выражений.
Уметь применять тригонометрические формулы при решении практических задач.
Овладеть понятием производной (возможно на наглядно - интуитивном уровне).
Освоить технику дифференцирования.
Уметь находить производную сложной функции.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально – экономических и физических, на наибольшее и наименьшее значения, на прохождение скорости и ускорения.
Уметь производить вычисления с действительными числами.
Уметь выполнять преобразования тригонометрических выражений.
Уметь решать алгебраические, тригонометрические уравнения, неравенства и их системы, применяя различные методы их решений.
Знать основные свойства функций и уметь строить их графики. Уметь применять свойства функций при решении различных задач.
Овладеть понятием непрерывности функций, понятием производной.
Освоить технику дифференцирования. Уметь находить производную сложной функции.
Освоить технику дифференцирования. Уметь находить производную сложной функции.
Научиться применять дифференциальное исчисление для исследования элементарных и сложных функций и построения их графиков.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уровень обязательной подготовки выпускника
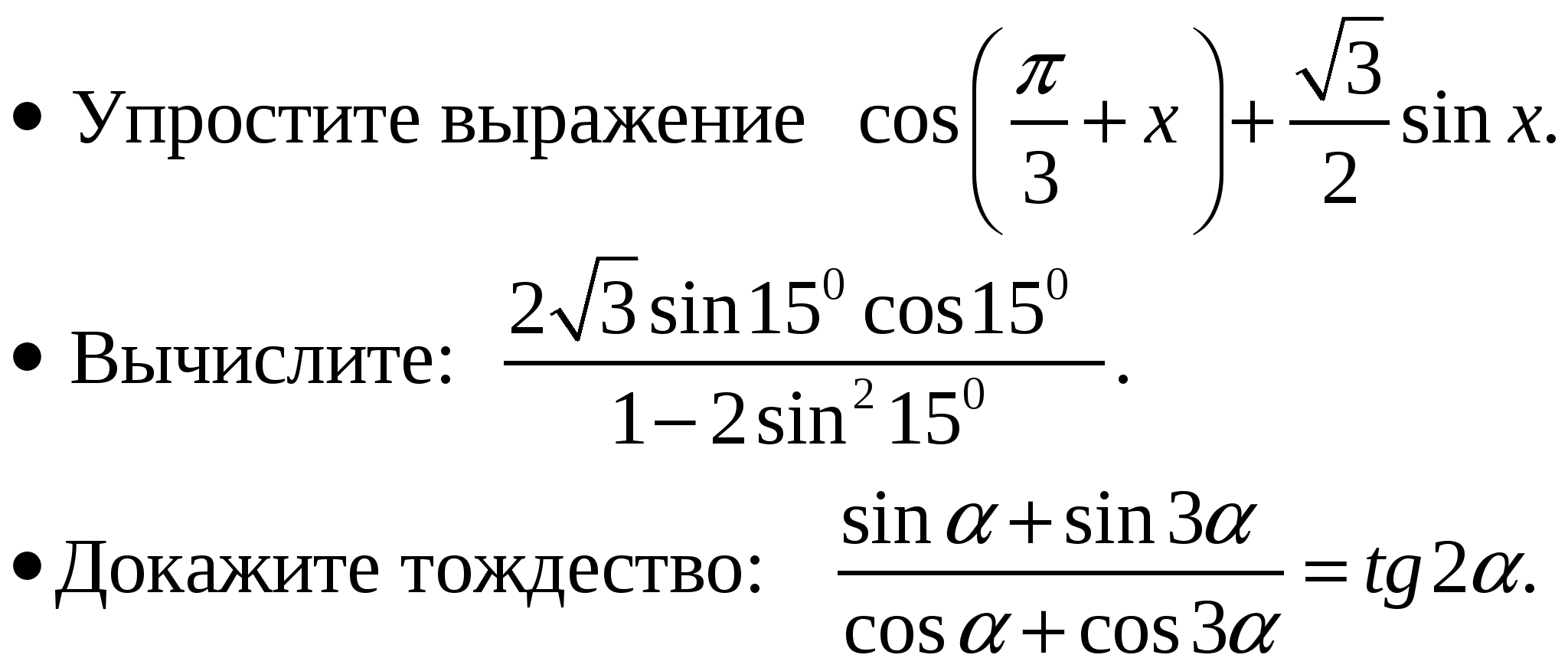
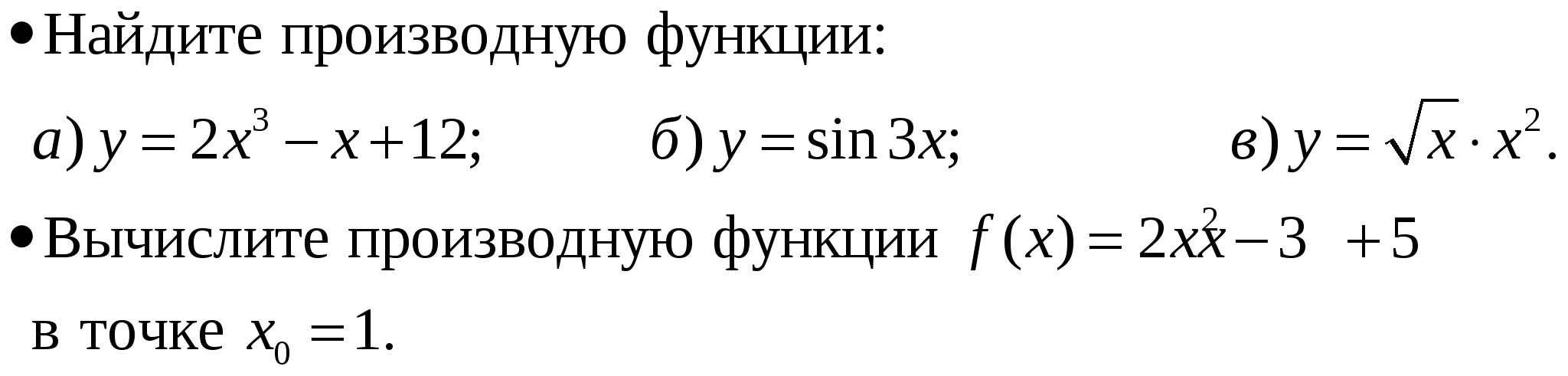
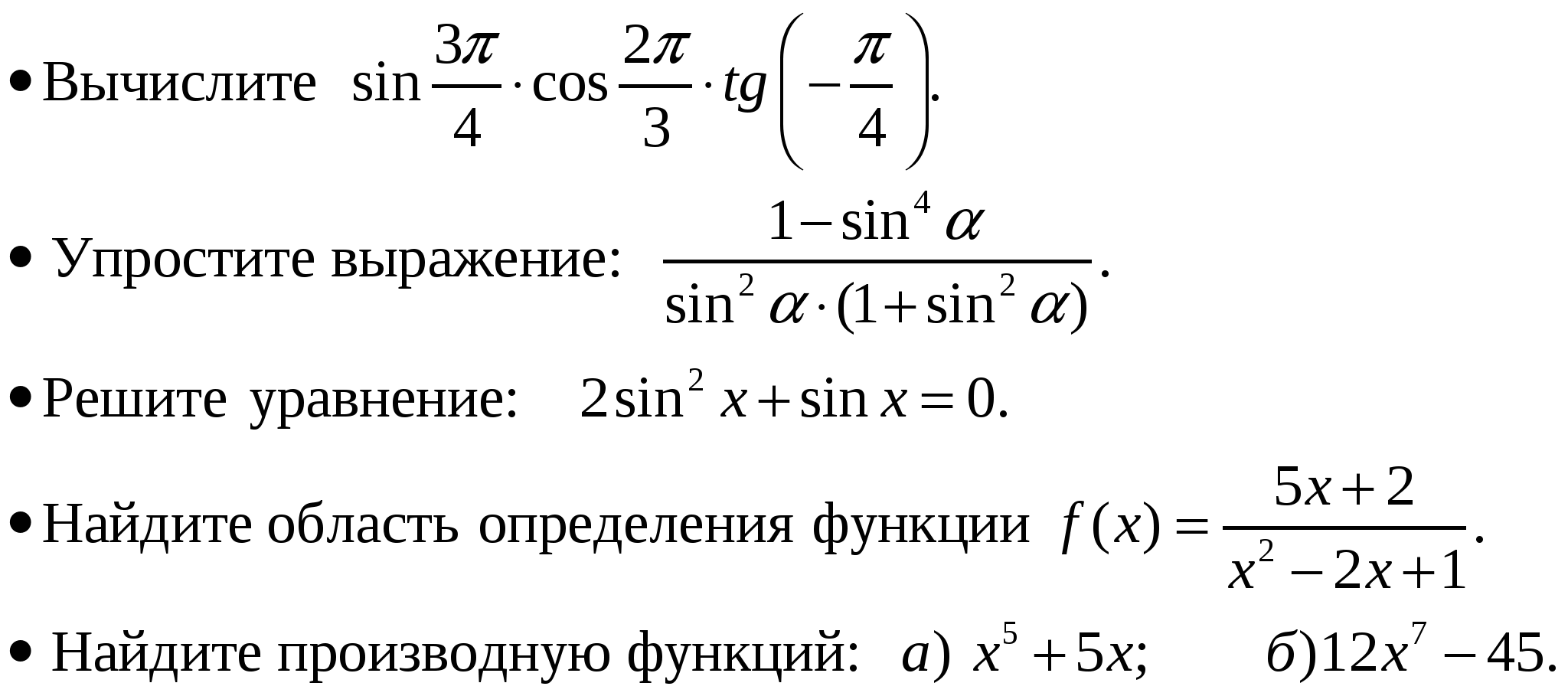
Уровень возможной подготовки выпускника
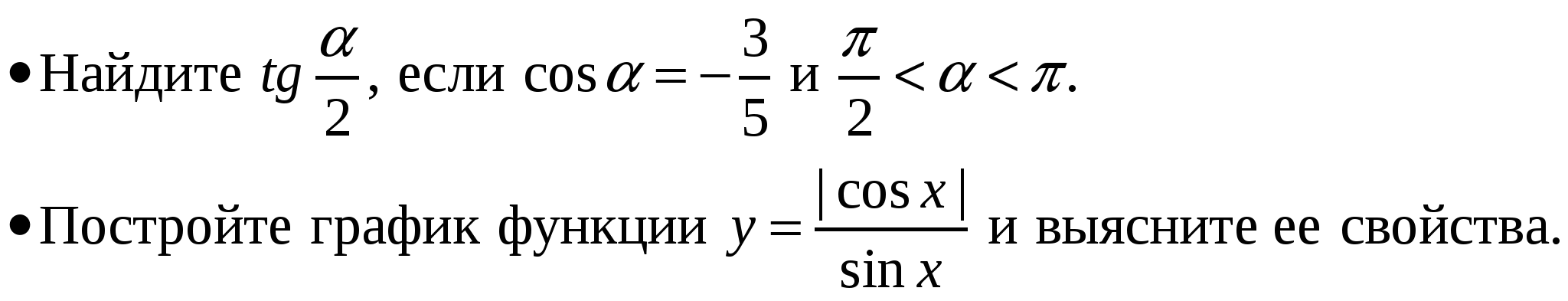
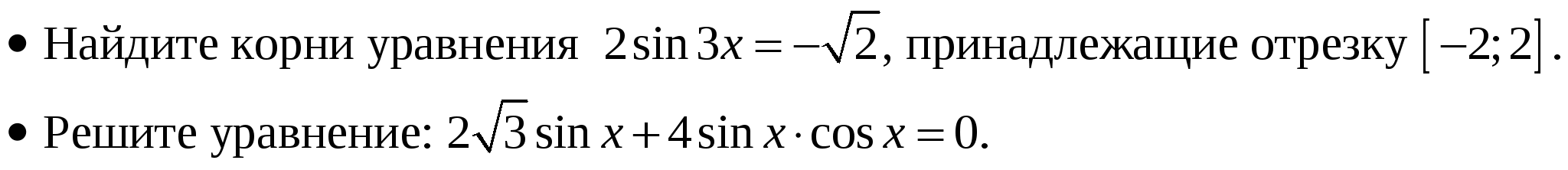 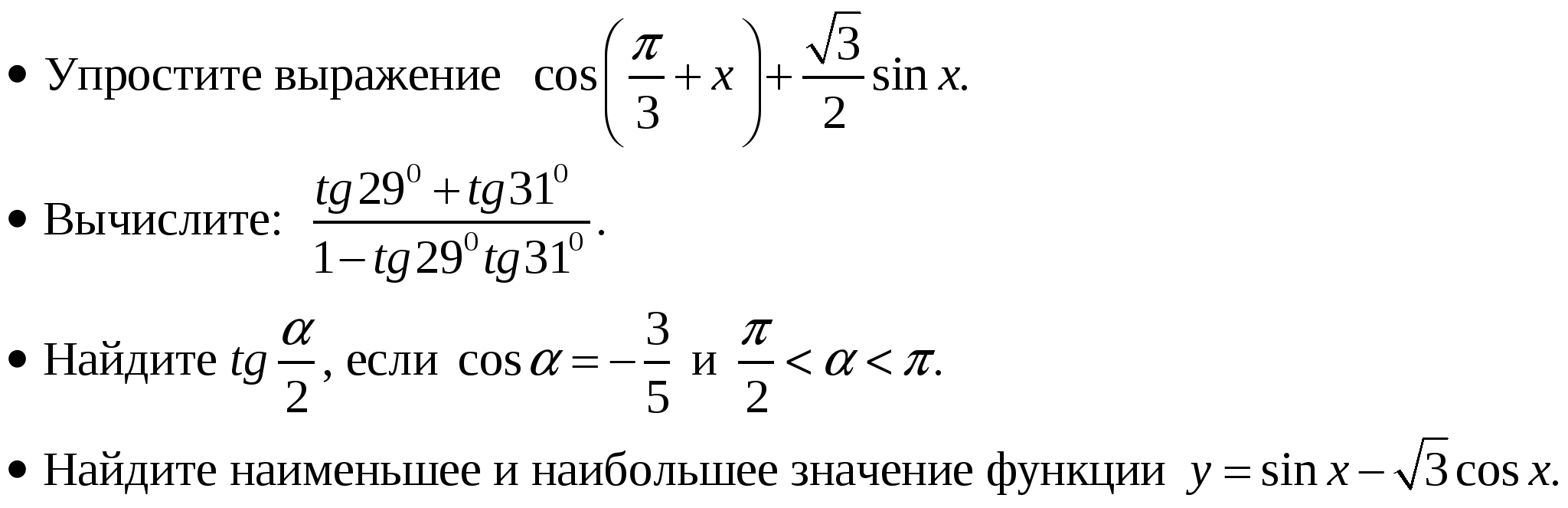
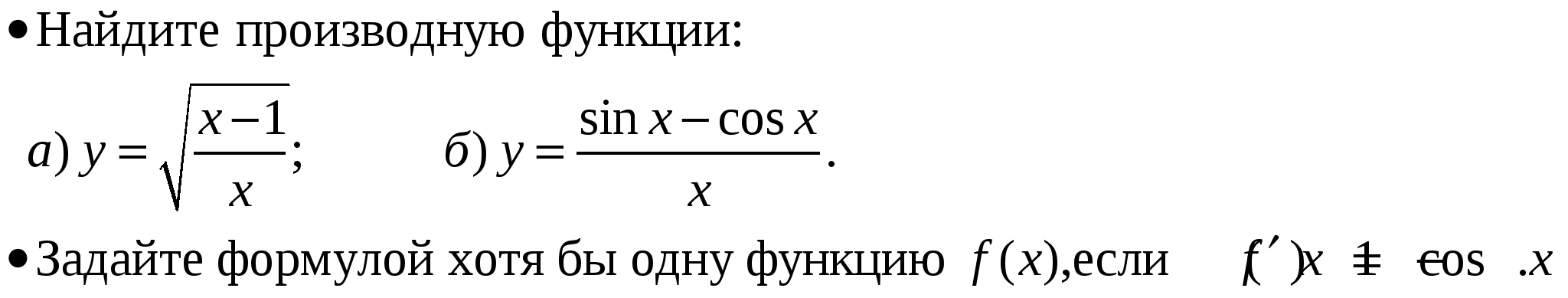
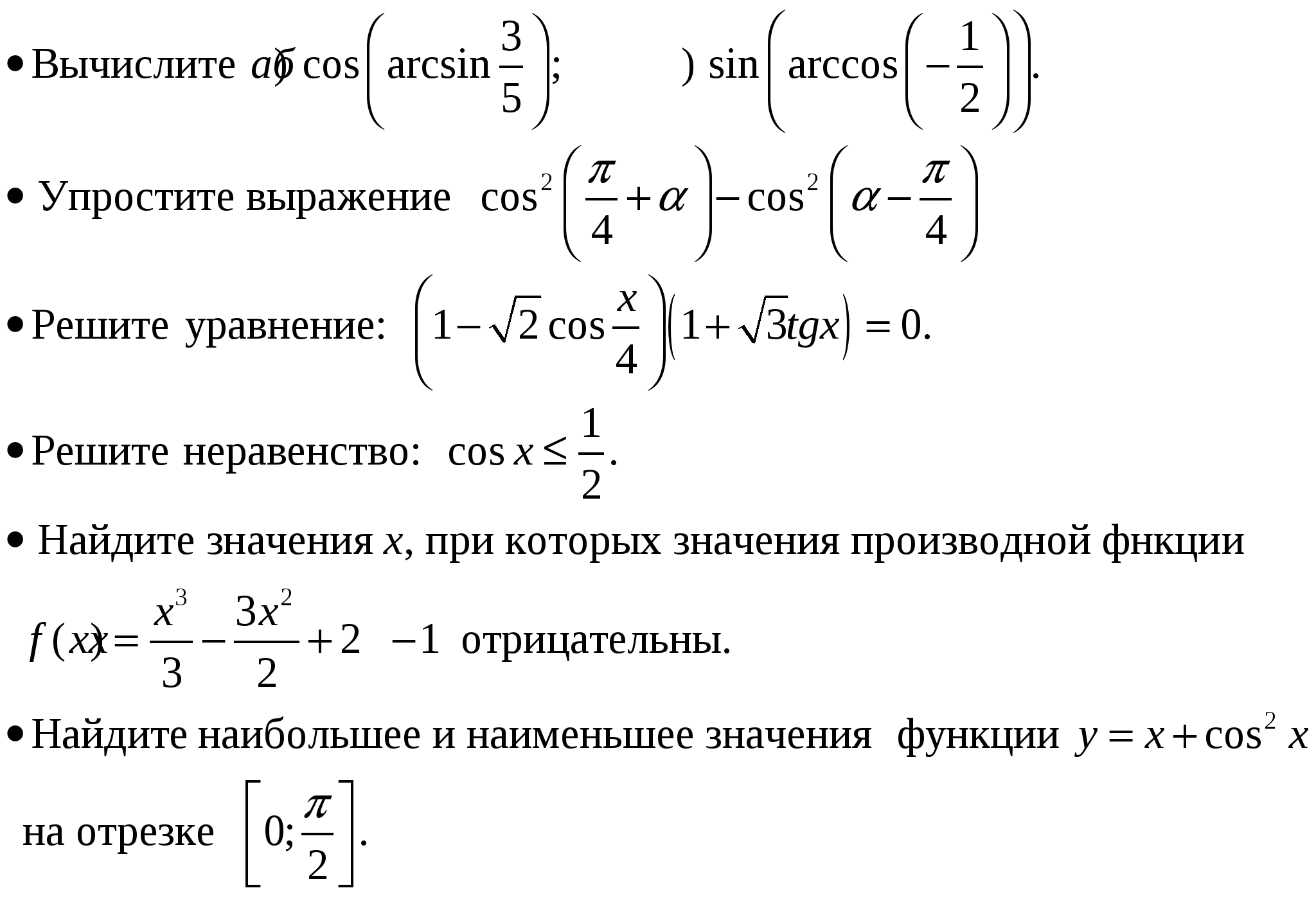
Литература
Мордкович А.Г. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. М., «Мнемозина», 2010.
Мордкович А.Г., Мишустина Т.Н. Тульчинская Е.Е. Алгебра и начала анализа. 10 - 11 классы. Задачник для общеобразовательных учреждений. М., «Мнемозина», 2010.
А.Г. Мордкович Алгебра и начала анализа.10-11.Методическое пособие для учителя. – М.: Мнемозина, 2005.
Дорофеев Г. В. и др. Оценка качества подготовки выпускников средней (полной) школы по математике. М., «Дрофа», 2002.
Концепция модернизации российского образования на период до 2010// «Вестник образования» -2002- № 6 - с.11-40.
Концепция математического образования (проект)//Математика в школе.- 2000. – № 2. – с.13-18.
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119.
№/
урока
|
Название темы урока
|
пункты
|
Сроки
|
Основные понятия, термины
|
Цели и задачи обучения
|
Примечания.
Диагностика.
ИКТ
|
|
Вводное повторение (7 часов)
|
|
1-7
7ч
|
Вводное повторение курса математики основной школы
|
|
|
|
Повторить и систематизировать знания учащихся по основным тема курса математики 7-9 классы
|
Срезовая контрольная работа
|
|
Введение (аксиомы стереометрии и их следствия) (5часов)
|
|
8
1ч
|
Предмет стереометрии. Аксиомы стереометрии.
|
1,2
|
|
Плоскость, аксиома
|
Изучить основные аксиомы плоскости
|
|
|
9-10
2ч
|
Некоторые следствия из аксиом
|
3
|
|
|
Умение доказывать некоторые следствия из аксиом
|
|
|
11-12
2ч
|
Решение задач на применение аксиом стереометрии и их следствий
|
1-3
|
|
|
Выработать навыки применения аксиом стереометрии и их следствий при решении задач
|
Самостоятельная работа №1
|
|
Глава I. Параллельность прямых и плоскостей (19 часов)
§1. Параллельность прямых, прямой и плоскости (5часов)
|
|
13
1ч
|
Параллельные прямые в пространстве. Параллельность трех прямых.
|
4,5
|
|
Скрещивающиеся прямые
|
Изучить взаимное расположение двух прямых в пространстве. Ввести понятие параллельных и скрещивающихся прямых
|
|
|
14
1ч
|
Параллельность прямой и плоскости.
|
6
|
|
Параллельность прямой и плоскости
|
Изучить возможные случаи взаимного расположения прямой и плоскости в пространстве
|
|
|
15-17
3ч
|
Решение задач на параллельность прямой и плоскости
|
4-6
|
|
|
Выработать навыки решения задач на параллельность прямой и плоскости
|
Домашняя контрольная работа
|
|
|
|
|
|
|
§2. Взаимное расположение прямых в пространстве. Угол между двумя прямыми (5часов)
|
18
1ч
|
Скрещивающиеся прямые.
|
7
|
|
|
Изучить признак скрещивающихся прямых и теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой и применять их на практике
|
|
19
1ч
|
Углы с сонаправленными сторонами. Угол между прямыми
|
8, 9
|
|
|
Изучить теорему об углах с сонаправленными сторонами и применять ее при решении задач
|
|
20-21
2ч
|
Решение задач по теме «Параллельность прямой и плоскости»
|
4-9
|
|
|
Повторить теорию, подготовить учащихся к контрольной работе.
|
Тест
|
22
1ч
|
Контрольная работа №1 на тему «Параллельность прямой и плоскости»
|
|
|
|
Контроль знаний учащихся
|
| |
|
|
 Скачать 381.8 Kb.
Скачать 381.8 Kb.