Уроках математики в общеобразовательной школе. Тема самообразования Учитель математики: рвачёвой анны викторовны г о. Балашиха 2013 г. Содержание
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
По ведущей ориентации: -тесты скорости, содержащие простые задачи, время решения которых ограничено настолько, что ни один испытуемый не успевает решить все задачи; -тесты мощности или результативности, включающие трудные задачи, время решения которых либо вовсе не ограничено, либо мягко лимитировано. Оценке подлежит успешность и способ решения задачи. Примером такого рода тестовых заданий могут быть задания для письменных итоговых экзаменов за курс школы; -смешанные тесты, которые объединяют в себе черты двух вышеперечисленных. В таких тестах представлены задачи различного уровня сложности от самых простых до очень сложных. Время испытания в данном случае ограничено, но достаточное для решения предлагаемых задач большинством обследуемых. Оценкой в данном случае служат как скорость выполнения заданий (количество выполненных заданий), так и правильность решения. Эти тесты наиболее часто применяются на практике, и именно к ним относится большинство тестов школьных достижений. 7. По степени однородности задач: -гомогенные, имеющие, как правило, одну шкалу, и позволяющие оценить одно свойство или качество личности; включают задачи, сходные по характеру, но различающиеся конкретным содержанием; -гетерогенные (многоразмерные), имеющие несколько шкал, и позволяющие оценить разнообразные характеристики личности; и включают задания, отличающиеся как по характеру, так и по содержанию. К этим заданиям относятся современные тесты школьных достижений. 8. По характеру действий: -вербальные (связанные с необходимостью произведения умственных действий — словесно-логические тесты, вопросники на проверку знаний, установление закономерностей и пр.); -невербальные (связанные с практическим манипулированием предметами - карточками, блоками, деталями). 9. По направленности, т.е. по тому, что именно предполагается изучать с помощью данного теста: тесты интеллекта, выявляющие особенности последнего; - личностные тесты (иногда называемые тестами темперамента), с помощью которых изучаются особенности личности испытуемого, предназначенные для диагностики мотивационно-потребностной сферы личности, позволяющие определить, на что направлена активность индивидуума и каким образом осуществляется им саморегуляция поведения; тесты настроений и состояний, направленные на изучение временных состояний, таких, например, как эмоции; - тесты достижений и другие. 10. По виду нормирования: - ориентированные на статистические нормы — тесты, основанием для сравнения, в которых служат соответствующим образом обоснованные статистически полученные значения выполнения данного теста репрезентативной выборкой испытуемых;
11. По характеру ответов на вопросы: - открытого типа (со свободными ответами — когда испытуемому необходимо самостоятельно дописать слово, словосочетание, предложение, знак, формулу и т.д.) - закрытого типа (с предписанными ответами — когда испытуемому необходимо выбрать из предложенных вариантов ответов тот или иной вариант). Типы тестовых заданий В настоящее время в нашей стране и, особенно, за рубежом накоплен значительный опыт применения тестовых заданий, в том числе и в средних учебных заведениях. Каждый тест, как правило, состоит из достаточно большого количества заданий, предназначенных для проверки тех или иных качеств тестируемых. Каждая классификация отражает то или иное представление о разнообразии форм тестовых заданий, а поэтому страдает определенной степенью односторонности. И это закономерно, поскольку данные классификации искусственные, и в их основе лежит признак, имеющий практическое значение для определения конкретных целей. Вместе с тем в ряде классификаций тестов в качестве основания для деления выбраны не наиболее существенные и важные в практическом отношении признаки, более того, часть из существующих классификаций не всегда подчинена всем правилам деления объема понятия. Поэтому такие классификации не выполняют в должной мере, возложенной на них главной задачи - облегчать процесс проверки степени усвоения знаний, не дают возможности быстро найти закономерности, которые определяют те или иные причины недостаточного усвоения знаний учащимися. Выделяют следующие возможные варианты ответов, используемые в тестах школьных достижений: открытого типа: задания дополнения (с ограничениями на ответы, с заданными ограничениями) — испытуемый должен сформулировать ответы с учетом предусмотренных в задании ограничений; свободного изложения, (свободного конструирования, без заданных ограничений) — испытуемый должен самостоятельно сформулировать ответы, ибо никакие ограничения на них в задании не закладываются. закрытого типа: - альтернативных ответов — испытуемый должен ответить да или нет; соответствия (на восстановление соответствия) - испытуемому предлагается восстановить соответствие элементов двух списков; - множественного выбора (ответы с вариантами выбора) — испытуемому необходимо выбрать, как правило, один правильный ответ из приведенного списка возможных ответов; - исключения лишнего (устранение лишнего элемента, «встретил лишнее — убери»); - аналогии — испытуемый должен выделить отношение аналогии между парами элементов (слов, свойств, качеств и т.д.); - последовательности (на завершение последовательности) испытуемый должен завершить некоторую последовательность элементов. Данная классификация дает достаточно полное представление о разнообразных формах тестовых заданий. Расскажем о ней более подробно. 1). Задания закрытого типа Эта форма заданий наиболее известна и чаще всего употребляется в практике тестирования. Такое задание состоит из двух частей:
Задания закрытой формы классифицируются по количеству приведенных ответов. Для того чтобы задания с несколькими вариантами выбора были эффективными, они должны отвечать следующим правилам:
испытуемых будут выполнять задание правильно. Метод получения эффективных дистракторов состоит в использовании неоконченного списка вариантов выбора и в последующем использовании неправильных ответов, записанных самими испытуемыми. Следует заметить, что в этой работе требуется осторожность. Необходимо убедиться, что предложенные дистракторы не вводят в заблуждение лучших испытуемых.
Существует и ряд других правил, большинство из которых обсуждаются в приведенных выше наиболее общих правилах. Сама проблема должна содержаться в основной части задания, а не выноситься в часть с вариантами выбора, которые должны быть настолько краткими, насколько это возможно. Оба эти момента относятся к правилу 1 -требованию простоты, а именно требованию того, что в основную часть должно быть включено лишь то, что необходимо для ясной и четкой формулировки проблемы. Кроме того, не стоит использовать задания с отрицаниями в основной части по двум причинам: а) это приводит к противоречиям (при чтении задания) и б) за исключением редких случаев, отрицательные значения не настолько важны как позитивные. Помимо перечисленного использование выражения «ни один из перечисленных» в качестве дистрактора допустимо только тогда, когда существует недвусмысленный правильный ответ, - как, скажем, в заданиях, связанных с алфавитом или математическими понятиями. Аналогично, использование в качестве дистрактора выражения "все перечисленные" приводит к допустимости скользких мест в формулировке заданий, в которых дистракторы не являются особенно дискриминативными, поскольку автор вопросов знает, что любой из ответов правильный. Приведем пример задания с несколькими вариантами выбора. Упростите выражение 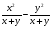 . .А. 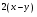 . Б. . Б. 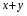 . В. . В. 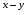 . Г. . Г. 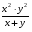 . .Данное задание удовлетворяет всем критериям, обсуждавшимся ранее. Математические упражнения - особенно подходящий предмет для тестирования, так как правильность ответа обычно не вызывает сомнения. Для учащихся, которые не уверены в том, как правильно открыть скобки, дистракторы являются, вероятно, весьма эффективными. Кроме того, дистракторы А) и Г) были использованы для того, чтобы избежать возможной подсказки правильного ответа (тем, что они длиннее, чем остальные). Задания с несколькими вариантами выбора являются наиболее широко используемыми. Это объясняется рядом преимуществ по сравнению с заданиями другого типа, которые мы будем обсуждать ниже. Итак, во-первых, каждое задание может быть высоконадежным. Поскольку возможен только один правильный ответ, отсутствуют факторы снижения надежности, связанные с субъективными оценками лиц, проводящих тестирование. Это свойство, по определению, присуще и другим эффективным заданиям, но не является из-за этого менее важным. Во-вторых, для таких заданий очень легко вычислять показатели. Это очень важно, особенно в больших по размерам тестах, а объём теста влияет на его надёжность. В-третьих, в заданиях с вариантами выбора, в которых дистракторы примерно эквивалентны, влияние угадывания на величину показателя сводится к вероятности 1/5, по сравнению с 50% для альтернативных заданий. В-четвертых, поскольку тесты с несколькими вариантами выбора оцениваются точными показателями, становится возможным получить точную оценку содержательности теста. Это важно при определении соответствия теста той группе испытуемых и той цели, для достижения которой он был создан. Отдельной строкой следует отметить задания закрытого типа, составленные с помощью альтернативности. Эта форма задания содержит обычно некоторое утверждение, которое испытуемый должен оценить как истинное или ложное (дать ответ «да» или «нет»). Выражение вида 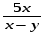
Задания такого типа обычно полезны при тестировании понимания отдельной темы или при очень подробной проверке знаний.
В данном случае достаточно подробно проверяется знание свойств показательной функции. Однако с заданиями альтернативного типа возникают определенные сложности:
2. Довольно сложно сформулировать утверждения, на которые можно дать недвусмысленный ответ «да» или «нет», а это особенно важно, так как вероятно, что наиболее сообразительные испытуемые увидят противоречия и могут не ответить на задание или дать неправильный ответ. 3. В связи с необходимостью точной формулировки утверждения возникает сложность с использованием таких слов, как «все», «каждый», «всегда», «никогда», в которых обычно может содержаться двусмысленность или противоречие. Подобно этому определяющие слова, такие как «иногда», «часто» понимаются испытуемыми настолько субъективно, что они вряд ли имеют фиксированное значение и, следовательно, приводят к нежелательным вариациям в ответах. Однако благодаря простоте, с которой данная форма заданий может быть применена для опроса понимания учебного материала, они заслуживают использования. 2). Задания на соответствие Эти задания предполагают наличие двух множеств, между элементами которых необходимо установить соответствие. Например, если мы хотим выявить знания испытуемого об авторах книг, одно множество должно содержать фамилии авторов, а другое - заглавия книг и между ними должно быть установлено правильное соответствие. Следует отметить один момент: список, из которого выбираются ответы, должен быть длиннее, чем первый список. В противном случае случайное угадывание станет все более и более вероятным. Так, если испытуемый знает четыре из пяти ответов в одинаковых по длине списках, то пятый неизбежно будет правильным. Поэтому следует предъявлять списки неравной длины или указывать, что некоторым элементам нет никаких соответствий (или то или другое). Эти меры с очевидностью уменьшают вероятность случайного угадывания правильного ответа. Пример: Если в окрестностях критической точки х0
3). Открытые задания В заданиях открытой формы в конкретное предложение необходимо вставить слово или дополнить его группой слов для завершения в виде верного высказывания. При составлении заданий открытой формы желательно соблюдение следующих правил: 1. В задании должно быть только одно дополнение, которое не допускает двойного толкования. Рассмотрим пример, при составлении которого это правило было нарушено. Четырехугольник, у которого стороны , являются В этом неудачно составленном задании предлагается заполнить три пропуска, которые отвлекают мысли учащихся от главного замысла автора теста, заставляют их вспоминать несколько определений, подходящих под указанный шаблон. При этом пробелы можно заполнить несколькими способами, например: 1.Четырехугольник, у которого противоположные стороны равны и параллельны, является параллелограммом. 2 Четырехугольник, у которого противоположные стороны попарно равны и параллельны, является параллелограммом. 3.Четырехугольник, у которого противоположные стороны попарно равны, является параллелограммом. 4.Четырехугольник, у которого только две противоположные стороны параллельны, является трапецией. Таким образом, возможность неоднозначных ответов ставит под сомнение целесообразность включения этого задания в тест. 2. Дополнять в предложении надо наиболее важное. Рассмотрим также, что может произойти, если это правило нарушено. Четырехугольник, у которого противоположные стороны параллельны, «является параллелограммом. Наличие дополнения не проверяет знание учащимся определения соответствующего понятия. При этом нетрудно заметить, что для пропущенного слова «попарно» трудно подобрать несколько правдоподобных значений. Это задание лучше было бы сформулировать так: Четырехугольник, у которого только две противоположные стороны параллельны, является параллелограммом. В последней формулировке проверяется четкое знание учащимися определения трапеции. При этом определения других четырехугольников не удовлетворяют указанному шаблону. 3. Дополнение должно быть словом, символом, формулой, но допускается и группа слов, когда она является, например, названием какого-либо понятия. Например: 1.Отрезок, соединяющий середины двух сторон треугольника, называется . 2. Площадь треугольника можно вычислить по формуле S= /2*0, При выполнении последнего задания ученик может дать несколько возможных ответов путем их перечисления. Соблюдением приведенных выше правил достигается превосходная надежность, а ответ считается правильным или нет без привлечения каких-либо субъективных суждений. В тесте открытых заданий должно быть немного, так как они, как правило, проверяют весьма узкий круг вопросов, связанных с репродуктивным воспроизведением учащимися формул, правил, алгоритмов, определений, а не способность человека к активному творческому мышлению. Задания на установление правильной последовательности В этих заданиях учащемуся предлагается какая-либо последовательность действий в случайном порядке. Он должен слева от каждого действия вместо прочерка проставить его порядковый номер в верной, по мнению учащегося, последовательности. Пример: Наибольший общий делитель двух чисел можно вычислить по алгоритму: 1 шаг: определить большее из чисел; 2 шаг: начать алгоритм сначала; 3 шаг: если числа равны, то любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма; 4 шаг: заменить большее число разностью большего и меньшего из чисел. Конечно, надо стремиться, чтобы эффект от наших заданий был максимальным. Каждый из описанных типов заданий наиболее эффективен при определенных условиях. Стандартным заданием, которое подходит к большинству видов материала и вопросов, является задание с вариантами выбора. Для получения подробной фактической информации, связанной с содержанием заданий, эффективный и компактный тест обеспечивается типом заданий на восстановление соответствия и альтернативными заданиями. Для тестирования понимания материала, представленного в вопросе, особенно полезны альтернативные задания. Исходя из этого, есть необходимость в заданиях всех типов, хотя и совсем необязательно, чтобы гест содержал одинаковое количество заданий каждого типа. Кроме того, разнообразие заданий, вероятно, сделает тест менее монотонным для испытуемых, что, в свою очередь, будет способствовать их меньшей утомляемости, которая зачастую служит источником ошибок. Критические замечания по ЕГЭ (математика) Проведение эксперимента по реализации программы Единого государственного экзамена вызывает неоднозначные оценки в среде научной и педагогической общественности России, и это вполне объяснимо, так как затрагиваются интересы значительных социальных групп: педагогов, руководителей органов образования, ректоров вузов, учащихся и их родителей. Накопленный опыт проведения эксперимента показал, что ЕГЭ чаще всего встречает противодействие по причинам политическим и единственный способ разрешить эти политические вопросы состоит в том, чтобы примирить стороны, заставив их уважительно выслушать друг друга, и принять такую структуру тестового экзамена, которая бы в наибольшей степени удовлетворяла максимальному числу требований и пожеланий всех участников процесса. Следует отметить, что в начале проведения ЕГЭ многие конкретные вопросы по структуре, содержанию, числу тестовых заданий, продолжительности проведения экзамена, технологии обработки результатов не были достаточно обоснованы. В последние годы постепенно ликвидируются указанные недостатки, в качестве примера следует отметить глубину идеологического обоснования общих подходов к разработке контрольно-измерительных материалов, предлагаемых Г.С. Ковалёвой [159]. Отметим некоторые недостатки по структуре и технологии ЕГЭ, которые повторяются из года в год при проведении эксперимента в России. Пермская область в числе 47 регионов страны в 2003 году также приняла участие в эксперименте: следует отметить, что в г. Перми (в Пермском классическом университете) тестовая форма экзамена используется с 1993 года, более того, в ПТУ в течение 10 лет проводился для всех желающих конкурс SuperTest, по результатам которого победители могли быть зачислены на механико-математический факультет и на специальность "математические методы в экономике" экономического факультета. Опыт проведения такого конкурса был признан положительным и вполне оправдал себя. Очевидно, что при получении искажённых результатов SuperTest'a, проводившегося 10 лет, они сразу же проявилось бы в процессе обучения студентов и факультеты отказались бы от их проведения. Предлагаемые на конкурсе тесты представляют собой набор 30 пятиальтернативных заданий, время выполнения тестов не превышало 70 минут, части типа В и С не использовались. В последние 5 лет аналогичные конкурсы проводились в Пермском филиале Государственного университет: Высшая школа экономики и головном университете ВШЭ (г. Москва), опыт был также признан удачным. Следует отметить ещё одно положительное последствие этих конкурсов: в г. Перми и Пермской области имеет место значительное повышение мотивации обучения математике, о чём свидетельствуют результаты Централизованного тестирования по математике I, математике II и ЕГЭ 2003 года - они выше средних по России. Перечислим некоторые из практически очевидных недостатков, искажающих объективность и достоверность результатов ЕГЭ.
З.Нет объяснения введения 4-х альтернатив ответа, хотя оптимальным считается число их равное пяти. 4. Нельзя признать идеальной форму бланка автоматизированного считывания информации сканером. Полученное при этом изображение обрабатывается программой FineReader. Теоретически это выглядит Достаточно хорошо, в работе [76] нет никаких сведений о проценте учащихся, которые заполняли бланки таким образом, что считывание осуществлялось с погрешностями, которые обязательно появлялись и процент их значителен (в подтверждение этого тезиса достаточно вспомнить сколько лет нас пытаются обучить правильно писать номера почтовых индексов, та же проблема возникает и у учащихся при написании, например, цифры 1 и 7). Почему бы не использовать положительный опыт штриховки овалов, используемый на протяжении нескольких лет в международных математических соревнованиях школьников «Кенгуру»? Форма бланка самым тесным образом связана с конфиденциальностью процедуры обработки. В ПФ ГУ ВШЭ используется бланк, состоящий из двух частей, разделенных перфорацией со штрихкодами и разделяемых сразу после заполнения Ф.И.О. абитуриента. Отсутствие Ф.И.О. на бланке ответа исключает возможность опознания автора на любом этапе проверки. Использование штриховки овалов обеспечивает 100% распознавание образов. «Гордостью» тестовых материалов Центра тестирования является наличие в тестах частей В, (где требуется вписывание количественного результата решения тестового задания) и части С (где требуется приведение полного решения). Общие замечания 1. Содержание и сложность части 2 вполне соответствует объявленному распределению заданий работы по сложности, изложенному в спецификации экзаменационной работы по математике для выпускников 11 класса, утвержденных 09.12.2002 года руководителем Департамента общего образования Минобразования РФ А.В. Баранниковым. 2. Нельзя признать, что заявленная в вышеуказанном документе трудность стереометрической задачи СЗ соответствует планируемой (2% - 3%), трудность предложенной задачи оказалась значительно ниже и расхождения экспертов при проверке были значительными. Первое задание части 3 С1 также нельзя признать соответствующим планированной трудности, оно явно проще и по трудности больше соответствует части 2 работы, при оценке этого задания также были расхождения у экспертов. Эти недостатки заданий С1 и СЗ неминуемо приводят к погрешности измерения, а расхождения в оценке заданий части С даже в 1 первичный балл при нормировании в 100-балльную шкалу приводит к расхождению уже в 3 балла. З.В вышеупомянутой спецификации указывается, что выполнение заданий части 2 (В7 - умение решать текстовые задачи и В8 - умение решать задачи на арифметическую и геометрическую прогрессии) не принимается во внимание при выставлении аттестационной оценки овладения курсом алгебры и начал анализа. С таким положением трудно согласиться школьникам, решившим эти задания; по вопросу исключения заданий по геометрии у учащихся никаких недопониманий нет, а исключение заданий В7 и В8 обосновать весьма сложно. 4.Расположение заданий частей 1 и 2 не согласуется с одним из основных принципов тестологии - от простого к сложному, так как: 1) любого учащегося надо ориентировать на успех; 2) очень добросовестные дети "застревают" на каком-либо задании, имеющему трудность, не соответствующую расположению в тесте. Следует признать неудачным подбор вариантов ответов. Обычно составители тестов тщательно отбирают варианты ответов, стремясь подобрать ответы, рассчитанные на типовые ошибки. Этот прием используется для более точного отбора грамотных учащихся и для борьбы с угадыванием ответов. Поясним это на примере следующего задания: Найдите производную функцию у = ех –х7
Любой школьник, знающий только лишь одно правило: "производная разности равна разности производных", безошибочно выберет правильный ответ 2), при этом ему совсем не обязательно знать таблицу производных. Попытки использовать типовые ошибки вычисления производных степенной и показательной функций оказываются здесь просто безуспешными. Спрашивается - почему бы вместо "+" в ответах 1), 2) и 4) не поставить "-", что является просто логичным. 6. Основной довод вузовских противников ЕГЭ - возможность угадывать ответы. Представленные ответы заданий части 1 А2, А5, А6, А9 очень ярко показывают, что ответы многих заданий можно угадать отбрасыванием явно непригодных. Укажем конкретные недостатки: А2 Выражение 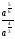 представьте в виде степени с основанием а. представьте в виде степени с основанием а.1) 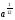 2) 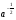 3) 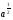 4) 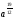 Ответы 1) и 4) неудачны, они не рассчитаны ни на какие-то типовые ошибки при выполнении действий над дробями и степенями, более уместными были бы ответы 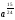 или или 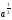 . .А9 Укажите промежуток,которому принадлежат корни уравнения 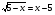 . .Не предусмотрен ответ, рассчитанный на типовую ошибку - появление Постороннего корня х = 4. А15 Укажите первообразную функции y = 2 sin 2x. 1)Y=4cosx + l 2)Y= -cos2x-2 3)Y= 2cosx 4)Y=2sin2x + 2 Почему-то не представлен ответ, рассчитанный на самую распространенную типовую ошибку 7 = cos2x + 2; ответы 1), 3) и 4) Школьниками, знающими хотя бы определение первообразной, отметаются сразу. Вышеупомянутые недостатки наглядно подтверждают один из доводов противников тестов и ЕГЭ - многие задания можно вообще не решать, а просто угадывать отбрасыванием совершенно непригодных и абсурдных ответов. Замечания по части 2 Все задания достаточно интересны, но не выдержан принцип составления теста: от простого к сложному. Задание В7 носит традиционный характер, его следовало поставить на место В4, задание В6 явно проще задания В5, которое было бы лучше сместить в конец части 2, задание В10 является достаточно сложным, его можно было поменять местами с геометрической задачей СЗ. Замечания по части 3 Задание С1 и СЗ явно не удовлетворяют продекларированным требованиям, предъявляемым к заданиям части 3, эти задания вполне можно было отнести к заданиям части 2, при проверке этих заданий было много расхождений в оценках экспертов из-за оформления. Задания С2 и С4 достаточно интересны. Представляется, что благие намерения введения части 3 в ЕГЭ, "для проверки состояния более сложных интеллектуальных и предметных умений -анализировать ситуацию, разрабатывать способ решения, проводить логически и математически грамотные рассуждения, обоснования, доказательства своих действий и грамотно записывать их" не могут быть практически реализованы по многим причинам. Заключение. Изменение общей ситуации современного образования ставит новые образовательные задачи перед школой, актуализирует роль и значение личности. Новые задачи требуют перестройки процесса обучения в школе. В содержание школьных предметов необходимо включить новые более теоретизированные знания на основе междисциплинарных связей. Перед современной школой ставятся новые цели: создание условий для формирования и полного осознания математики через развитие их индивидуальных качеств и способностей еще с начальных классов. Систематическая проверка знаний и умений учащихся - одно из основных условий повышения качества обучения. Учитель математики в своей работе должен использовать не только общепринятые формы проверки, но и систематически изобретать, внедрять свои средства проверки знаний учащихся. В процессе обучения математики учащиеся овладевают множеством математических понятий, их свойств, отношений и в результате проведения различных форм проверок учащиеся не только лучше усваивают материал, но и раскрывают свои индивидуальные способности. У учащихся повышается заинтересованность к учебе и уровень подготовки к уроку, что позволяет своевременно устранить недостатки и пробелы в знаниях учащихся. Сущность любой проверки знаний заключается в соответствии полученных результатов запланированным уровням усвоения. Решить проблему проверки знаний - найти объективный путь соотнесения достигнутых учащимися результатов с запланированными уровнями. Исследование системы проверки знаний, умений и навыков учащихся позволило решить поставленные задачи. Получены следующие выводы и результаты: 1. Функции проверки знаний учащихся многообразны. Так как основная цель проверки знаний - выявление и диагностика результатов образования, развития и воспитания, то основными функциями проверки, следовательно, должны быть функции, совпадающие с основными задачами этой части процесса обучения. Заключительная (итоговая) проверка знаний осуществляется на экзамене в 11 -ом классе. Ее цель - выявить общую систему знаний ученика, сформированных за все годы изучения предмета.
Успешность преподавания математики, как и остальных предметов школьной программы, определяют многие факторы, среди которых, как основной, выделяют выбор методики преподавания. Именно от правильного выбора методов и приемов преподавания каждой темы курса и их удачного сочетания, зависит уровень понимания, в конечном счете, учащимися материала. Современные тенденции в образовании заставляют нас по-иному относиться к процессу обучения. Влияние и включение новых технологий в образовательную деятельность привело к существенному и реальному сдвигу в сторону развивающей системы обучения. Но вместе с тем, несмотря на все позитивные стороны этих технологий, существует еще масса факторов, которая препятствует: - это, прежде всего, нежелание «старых» учителей переходить на новую систему («Зачем переходить если, работая в школе 10-15 лет уже сформировался основной, как правило узкий, методический аппарат?»); - это и недостаточное наличие методической литературы; - также это «обычные» классы по 20-25 человек, где понятное дело индивидуальный подход практически не осуществим; - это и жесткие рамки времени и программы и многое другое. Список литературы.
17.Российская педагогическая энциклопедия. Статья «Знание». - М.: Научное издательство «Большая Российская энциклопедия», Т. 1, 2005. С. 331.
20.Скаткин М.Н. Качество знаний учащихся и пути его совершенствования. М.: Педагогика, 2005.
Приложение 1. Отгадывание математических кросснамберов. Разгадывание кросснамберов следует предлагать учащимся для проверки их знаний по определенной теме. Предлагаемая карточка содержит кросснамбер, разгадать который можно, решив ряд задач. При этом работа интересна, нестандартна и не вызывает психического напряжения. В каждую клеточку вписывается по одной цифре. Правильность решения проверяется сразу: цифры, стоящие при пересечении горизонтали и вертикали, должны совпадать. Можно предложить учащимся составить кросснамберы на заданную тему. №1. Действия с натуральными числами. (5 класс)
По горизонтали. а) 36-527 м) 1000 - 38 г) 48-5 н) 600+20+3 е) 156+87 о) 832:8 и) 112 р)43-4 к) 38-2 с)6+(5-7+15:3)-500 По вертикали. а) 12386-12376 ж) 6541-58-41 6)5707680:6 з) 9966:3 в) 792:36 и) 57:3 г) 1130+1 л) 7-3-8 д) 39-68+1468 п) 900-858 р) 1000:20-34 Ответы. По горизонтали, а) 18972. г) 240. е) 243. и) 121. к) 131. м) 962. н) 623. о) 104. р) 132. с) 20006. По вертикали, а) 10. б) 951280. в) 22. г) 2261. д) 4120. ж) 4163. з) 3322. и) 19. л) 13. п) 42. р) 16. №2. Основные задачи на дроби. ( 5 класс).
По горизонтали. б) Найдите 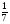 от числа 280. от числа 280.в) 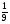 кг муки стоит 90 копеек. Сколько стоит 1кг муки? кг муки стоит 90 копеек. Сколько стоит 1кг муки?По вертикали. а) Найдите 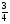 от числа 144. от числа 144.г) 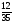 числа равны 36. числа равны 36.Чему равно число? Ответы. По горизонтали, б) 40. в) 810. По вертикали, а) 108. г) 105. №3. Задачи на проценты. (5 класс)
По горизонтали. а) Сколько процентов составляет число 4 от числа 5? б) Расстояние между пунктами А и В 90 км. 20% пути туристы проехали на автобусе. Сколько км туристы проехали на автобусе? г) Найдите 15%) от числа 400 По вертикали. а) Найдите число, 10%> которого составляют 84,1 в) 40%) учащихся школы обучаются на "4" и "5". Сколько учащихся в школе, если "хорошистов"320 человек? Ответы. По горизонтали, а) 80. б) 18. г) 60. По вертикали, а) 841. в) 800. Приложение 2. Образец проверочной работы по теме "Четырехугольники" 1. Может ли сторона ромба равняться половине его диагонали? 2. Верно ли утверждение: " Четырехугольник, у которого две стороны параллельны, а две другие равны, является параллелограммом"?
5. Верно ли, что четырехугольник со взаимно перпендикулярными и конгруэнтными диагоналями обязательно является квадратом?
8. Верно ли, что параллелограмм со взаимно перпендикулярными диагоналями является ромбом? 9. Верно ли высказывание: "Для того чтобы четырехугольник имел равные диагонали необходимо, чтобы он был прямоугольником или трапецией"? Проанализировав итоги контрольной работы и выяснив число правильных и ошибочных ответов по каждому из предложенных в работе вопросов, учитель может получить достаточно ясную картину того, что плохо его ученикам, и соответственно внести коррективы в свою работу со всем классом или с отдельными учащимися. Приложение 3. 1. Равенства и неравенства В таб. № 1 поставьте букву И там, где получается истинное высказывание, и букву L там, где ложное.
В таб. № 2 поставьте букву И там, где получается истинное высказывание, и букву L там, где ложное.
2. Уравнения и неравенства Таблица № 3
Заполните пустые места в таб. № 3. При каком X значение первого выражения а) больше значения второго б) меньше значения второго в) равно значению второго Приложение 4. Тест по теме «Сокращение алгебраических дробей». Вариант 1.
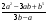 , если , если 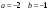 . .А. 1. Б.-1. В.-2. Г.0.
А.(1; 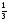 ) Б.(3;-1) В.(-3;1) Г.( ) Б.(3;-1) В.(-3;1) Г.(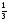 ; 1) ; 1)
А. 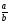 . Б. . Б. 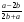 . В. . В. 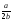 . Г. . Г.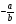 . .
1) 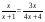 3) 3)  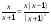 2) 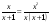 4) 4) 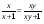 ? ?А. Первое. Б. Второе. В. Третье. Г. Четвертое.
А. 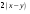 . Б. . Б. 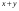 . В. . В. 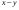 . Г. . Г. 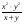 . .Вариант 2. 1. Найдите значение алгебраической дроби 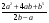 , если , если  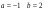 . .А. -5. Б. 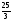 . В. . В.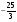 . Г.5,2. . Г.5,2.2. Какая пара значений ( 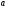 ; ; 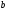 ) из четырех, указанных ниже, является недопустимой для дроби ) из четырех, указанных ниже, является недопустимой для дроби 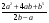 ? ?А.(-2; 1) Б.(2;-1) В.(1; 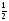 ) Г.( ) Г.(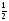 ; 1) ; 1) 3. Сократите алгебраическую дробь 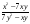 . . А. 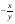 . Б. . Б. 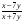 . В. . В. 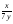 . Г. . Г.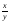 . .4. Какое из написанных четырех равенств является тождеством: 1) 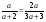 3) 3)  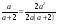 2) 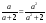 4) 4) 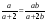 ? ?А. Первое. Б. Второе. В. Третье. Г. Четвертое. 5. Упростите выражение 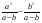 . .А. 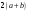 . Б. . Б. 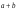 . В. . В. 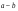 . Г. . Г. 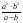 . .Такие задания вызывают интерес у учащихся и способствуют формированию умения читать схемы и таблицы. Проверочные задачи в виде таблицы и тестов являются лишь одним из видов осуществления эффективной проверки. Также есть и другие виды проверки знаний. Такие как контрольные работы, математические диктанты, вставить пропущенное слово, не соответствие и другие. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
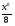
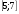
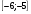
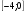
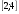
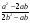 .
. 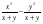 .
.