Арифметический способ решения задач на смеси и сплавы
 Скачать 58.9 Kb.
|
Арифметический способ решения задач на смеси и сплавы. Задачи, которые мы будем решать, относятся к традиционным задачам математики. Они охватывают большой круг ситуаций: смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Когда-то они имели исключительно практическое значение. В настоящее время эти задачи часто встречаются в тестах на выпускных экзаменах и на вступительных экзаменах в вузы.Мы рассмотрим задачи на смешивание, которые можно решить не только алгебраически, то есть с помощью уравнения, но и арифметическим способом. Для успешной работы нам понадобится повторить основные понятия этой темы. Ход урока I. Фронтальная работа с классом. 1. Сформулируйте определение концентрации. (Слайд 1) (Концентрация вещества в смеси – это часть, которую составляет масса вещества в смеси от массы смеси) Нахождение части от целого. В химии вы называли эту величину массовой долей вещества. Концентрация вещества может быть указана и числом и %. 2. Объясните значение высказываний: (Слайд 2) а) Концентрация раствора 3 %; (В 100 г раствора содержится 3 г вещества). в) Молоко имеет 1,5 % жирности; (В100 г молока содержится 1,5 г жира). с) золотое кольцо имеет 583 пробу? (В1 г кольца содержит 583 миллиграмма золота). Сколько сахара содержится в 200 г 10%- го сахарного сиропа? Теперь давайте попробуем решить устно несколько задач. 3. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора? (1: 5 ·100 = 20 %) (Слайд 3) 4. Килограмм соли растворили в 9 л воды. Какова концентрация раствора? (1 : 10 ·100 = 10%) (Слайд 4) II. Решение задач Конечно, вы понимаете, что не все задачи можно решить устно. Следующую задачу мы решим с вами с помощью уравнения. №1. В каких пропорциях нужно смешать раствор 50 % и 70 % кислоты, чтобы получить раствор 65 % кислоты? (Слайд 5) Для решения задачи я попрошу вас заполнить таблицу, которая находится у вас на столе.
(Слайд 6) Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов. Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов. Тогда масса смеси будет (х + у) г. Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-ом растворе. Это 0,5х г, во втором растворе 0,7у г, а в смеси будет 0,65(х + у) г кислоты. По условию задачи составим и решим уравнение. (Слайд 7) 0,65 (х + у) = 0,5 х + 0,7 у, 65 х – 50 х = 70 у – 65 у, 15 х = 5 у, 3 х = 1 у, х : у = 1 : 3. Нужно взять: 1 часть раствора 50% кислоты и 3 части раствора 70% кислоты Ответ: 50% раствора кислоты -1 часть, 70% раствора кислоты - 3 части. А теперь я хочу предложить вам схему решения этой задачи арифметическим методом, который позволяет решить ее практически устно. Запишем концентрацию каждого раствора кислоты и концентрацию смеси так: 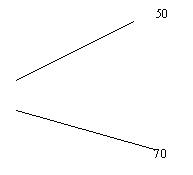  Вычислим, на сколько концентрация первого раствора кислоты меньше, чем концентрация смеси и на сколько концентрация второго раствора кислоты больше, чем концентрация смеси и запишем результат по линиям: (Слайд 8) 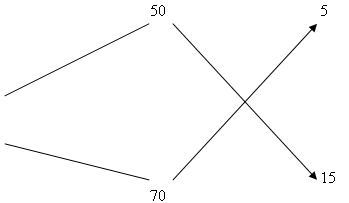 Таким образом, 5 частей нужно взять 50% раствора кислоты и 15 частей 70% раствора кислоты, то есть отношение взятых частей  . Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части. Сравните полученные результаты. Делаем вывод: получили один и тот же ответ, но времени затратили гораздо меньше.Вовсе не случайно в старые времена отношение масс смешиваемых вещей находили таким образом. Но вряд ли все ученики, получавшие правильные ответы описанным способом, понимали тогда смысл выполняемых действий. Докажем справедливость этого способа. В каких пропорциях нужно смешать растворы а % и b % кислот, чтобы получить раствор с % кислоты? Заполним вторую таблицу. (Слайд 9)
Заполняем 1-й столбик. Здесь мы указываем концентрацию растворов. Заполняем 2-й столбик. Здесь мы указываем массу каждого раствора. Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов. Тогда масса смеси будет (х + у) г. Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-м растворе. Это 0,01·ах г, во втором растворе 0,01·bу г, а в смеси будет 0,01·c(х + у) г кислоты. Составим и решим уравнение (Слайд 10) 0,01·c(х + у) = 0,01·ах + 0,01·bу, cx +cy = ax + by х(с – а) = у(b – c),  Заполним схему, учитывая, что а < c < b. 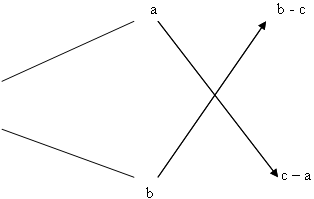 Теперь понятно, почему эта схема давала правильные результаты. Давайте применим этот способ для решения задач. №2. В каких пропорциях нужно сплавить золото 375 пробы с золотом 750 пробы, чтобы получить золото 500 пробы? (Слайд 11) Итак составляем схему. (Слайд 12) 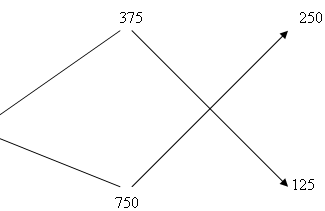 Чтобы получить золото 500 пробы нужно взять: 2 части золота 375 пробы и 1 часть золота750 пробы. Решим следующую задачу. №3. Морская вода содержит 5 % соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5 %? (Слайд 13) (Слайд 14) 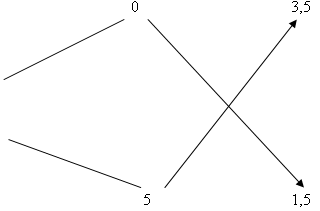  Нужно взять 7 частей пресной воды и 3 части морской воды. По условию нам известно, что морской воды 30 кг и это 3 части нового раствора. Значит на одну часть приходится 10 кг. Следовательно 7частей пресной воды – это 70 кг.Ответ: нужно добавить 70 кг пресной воды. А теперь я попрошу вас составить задачу на смешение и решить ее алгебраическим способом. (Самостоятельная работа). Какие это могут быть задачи? На смешение товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Запишите условие задачи, приведите схему решения и решите ее. Несколько лучших задач мы рассмотрим на доске. Подведем итог урока. Сегодня мы познакомились с алгебраическим способом решения задач на смешение. Конечно, не все задачи можно решить этим способом, но я думаю, что вам интересно было познакомиться с ним. |