Урок по алгебре в 8 классе по теме: «Решение квадратных уравнений»
 Скачать 93.22 Kb. Скачать 93.22 Kb.
|
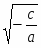 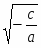 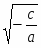 Урок по алгебре в 8 классе по теме: «Решение квадратных уравнений». Урок по алгебре в 8 классе по теме: «Решение квадратных уравнений».Цели урока: образовательная – формирование умения обобщать типы квадратных уравнений и способы их решения; формирование навыка выбора рационального способа решения квадратного уравнения; развивающая – развитие интереса к предмету, активизация мыслительной деятельности, развитие творческого мышления, математической речи; воспитательная – формирование умения работать самостоятельно и в паре; умение задавать вопросы; понимать другое решение. Задачи для учащихся: 1. Знать формулы для решения квадратных уравнений. 2. Различать типы квадратных уравнений и знать способы их решения. 3. Уметь решать квадратные уравнения. Тип урока: урок обобщения и систематизации знаний по теме «Квадратные уравнения». Ход урока. . Организационный момент. Постановка целей урока. Сегодня мы проводим урок-тренинг, на котором вы, ребята, повторите и систематизируете методы решения разных видов квадратных уравнений. Вы должны научиться выделять виды квадратных уравнений и способы их решения, а также уметь выделять наиболее рациональный способ решения. . Устная работа. 1. Проклассифицируйте уравнения по какому-то признаку и выделите лишнее уравнение: а) 2х – х2 = 0 а) х2 – 9х +20 = 0 а) х2 – 4х + 7 = 0 б) 4х2 – 9 = 0 б) 9х2 – 6х + 10 =0 б) 2х2 – 5х + 19 = 0 в) 3х2 – х – 3 = 0 в) х2 + 5х – 1 = 0 в) 3х2 + 32х + 60 = 0 г) 3х2 + 2 = 0 г) х2 + 4х – 2 = 0 г) х2 + 12х + 32 = 0. 2. Решите уравнения: а) х2 + 3х – 4 = 0 (1 и -4) ( а + в + с = 0, то х1 = 1, х2 =   ) )б) х2 – 4х + 3 = 0 (1 и 3) в) 7х2 – 9х + 2 = 0 (1 и  ) )г) 5х2 – 8х + 3 = 0 (1 и 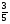 ). ).. Решение задач. 1. На экране таблица и у каждого ученика на столе такая же таблица. Задание. Каждое уравнение на экране впишите в таблицу, соответствующее указанному признаку и решите его в своих тетрадях. 1) х2 + 36 = 0 2) 5х2 – 6х – 8 = 0 3) 2х2 = 0 4) 5х2 – 8х + 3 = 0 5) (х – 2) (х + 3) = 0 6) х2 – 4х + 4 = 0 7) х2 – 6х + 8 = 0 8) 5х2 + 4х = 0 9) 2х2 + 3х + 1 = 0 10) 2х2 – 5х + 2 = 0 11) 7х2 – 3 = 0
Обсуждение таблицы (работа в парах) При обсуждении работы в парах, ученики сверяют свои ответы, просматривают способы решения, выбирают наиболее рациональный способ и обсуждают общий способ решения квадратных уравнений. У учеников появляется возможность проговорить способ решения, объяснить свой способ , что требует активной речевой деятельности, развивает умение слушать и понимать решение товарища, понимать общее решение. Учитель проверяет с помощью кинопроектора решения уравнений. Ученики обосновывают свой выбор уравнений и обсуждают способы их решения. Таким образом, все уравнения классифицируются. Выделить уравнение 5) (х – 2) (х + 3) = 0, корни 2 и -3. Разложение квадратного трехчлена на множители в 9 классе будем изучать более подробно.
2. Задание. Найдите ошибку в решении и подчеркните ее. (У учащихся на столе карточки по одной на парте) 1) 2х2 – 5х – 3 = 0 2) х2 + 5х – 6 = 0 D = 25 -423 = 1 D = 25 -41(-6) = 49 х1 =  = = 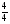 = 1 х1 = = 1 х1 = 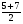 = 6 = 6х2 = 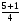 = = 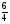 = 1,5 х2 = = 1,5 х2 = 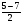  = -1 = -1Ответ: 1 и 1,5 Ответ: 6 и – 1. 3) 5х + х2 – 6 = 0 D = 1 - 45(-6) = 121 х1 = 3; х2 = - 8 Ответ: 3 и – 8. Первый вариант решает, второй проверяет у первого. Затем проверяем с помощью кинопроектора. Обсуждаем. 1) 2х2 – 5х – 3 = 0 2) х2 + 5х – 6 = 0 D = 25 -423 = 1 D = 25 -41(-6) = 49 х1 =  = = 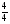 = 1 х1 = = 1 х1 = 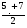 = 6 = 6х2 = 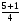 = = 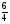 = 1,5 х2 = = 1,5 х2 = 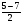  = -1 = -1Ответ: 1 и 1,5 Ответ: 6 и – 1. 3) 5х + х2 – 6 = 0 D = 1 - 45(-6) = 121 х1 = 3; х2 = - 8 Ответ: 3 и – 8. 3.Самостоятельная работа.
Ответы проверяем в таблице.
4. Историческая справка. (Сообщение делает учащийся из учебника «Алгебра 8», страница 211) V. Задание на дом. Учащимся раздаются карточки с заданием: «Провести исследование и установить связь между коэффициентами квадратного уравнения и его корнями у следующих уравнений: 1) 6х2 – 13х + 6 = 0, 2) 5х2 - 26х + 5 = 0, 3) 2х2 + 5х + 2 = 0, 4) 4х2 + 17х + 4 = 0, 5) 3х2 – 10х + 3 = 0 . V. Итог урока. 1) Оценки за урок. 2) Вывод: Чтобы решать квадратные уравнения, нужно знать формулы – это обязательно. Но, чтобы быстро и устно решать некоторые уравнения, нужно умение анализировать. Если хорошо потренироваться, то решение любого уравнения не вызывает затруднений.
|

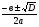 , где D = в2 – 4ас
, где D = в2 – 4ас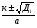 ,
, 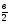
 )2 =
)2 = 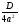
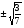

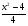 =
= 
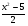 =
= 
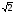 )
)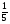 )
)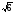 )
)