Тема. Вычисление объема прямоугольной призмы по площади основания и высоте бокового ребра. Основные цели

Название	Тема. Вычисление объема прямоугольной призмы по площади основания и высоте бокового ребра. Основные цели
Дата	11.03.2016
Размер	50.3 Kb.
Тип	Документы

Тема. Вычисление объема прямоугольной призмы по площади основания

и высоте бокового ребра.

Основные цели:

- формирование совокупности компетенций, необходимых для вычисления объёма прямоугольника;
- развивать мыслительные операции;
- воспитывать прилежание, аккуратность, стремление к выполнению всех заданий; уважение друг к другу;
Формировать ОУНН:
-оформлять свои мысли в письменной речи;
- самостоятельно формулировать цели урока после предварительного обсуждения;
- продолжать работу по формированию социальных компетентностей: понимать, излагать, выделять главное в информации.

Тип урока: урок открытия нового знания

1. Мотивация к учебной деятельности (организационный момент).

Эпиграф.

Кто с детских лет занимается математикой,

Тот развивает внимание, тренирует свой мозг, волю, воспитывает настойчивость и упорство в достижение цели…

Алексей Иванович Маркушев – педагог, доктор математических наук, профессор.

-Эпиграфом к уроку я взяла слова Алексея Ивановича Маркушева. Прочитайте.

-Как вы понимаете смысл этого высказывания?

-Какие качества личности помогут нам для достижения цели урока?

2. Актуализация знаний и фиксация затруднения в деятельности.

$c:\users\елена\desktop\img_0002.tif$

10

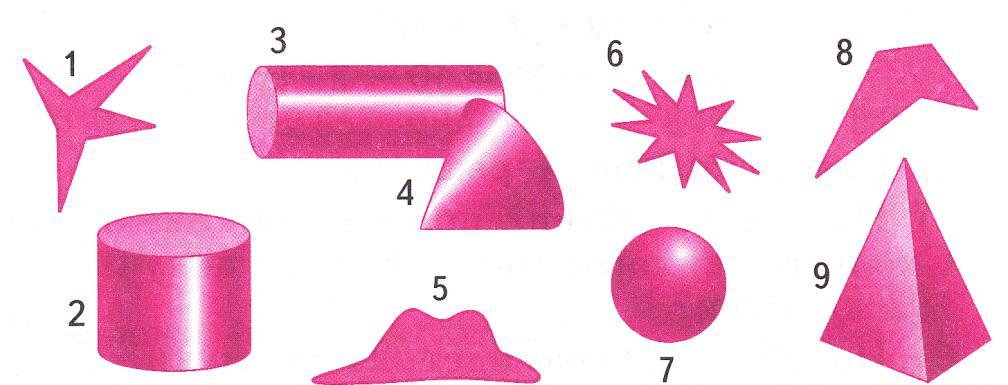
1.Разделите фигуры на две группы. Назовите фигуры каждой группы.

Назовите объёмные тела , имеющие: два основания,

одну вершину, одно основание, многоугольное основание.

2. Тест на знание и быстроту реакции.

- Эта величина показывает, сколько места занимает предмет в пространстве.

-Прямоугольная призма с равными ребрами, это?

-Сумма всех сторон прямоугольника, это?

-Куб с ребром 1 см, это?

3. Постановка учебной задачи.

м, дм², мм², км, м³, дм, см³

Разделите данные единицы измерения величин на три группы.

В каком соотношении находятся м и км, дм и км, дм² и мм², м³и см³

Назовите величины, которые измеряются единицами каждой группы.

Под каждой фигурой запишите формулу нахождения величин.

Назовите тему, над которой мы работаем. Сегодня нам предстоит преобразовать формулу нахождения объёма прямоугольной призмы.

Поработайте в парах, обсудите: может быть, кто-то знает, как преобразовать формулу нахождения объёма прямоугольной призмы?

4. Построение проекта выхода из затруднения («открытие» детьми нового знания).

1) Какую площадь (в квадратных сантиметрах) имеет прямоугольник на рисунке?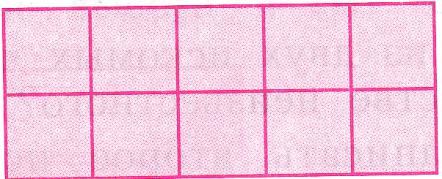 $c:\users\елена\appdata\local\microsoft\windows\temporary internet files\content.word\img.tif$

2) Сколько кубиков с ребром 1 см поместится в коробке, основание которой равно данному прямоугольнику, а высота 1 см?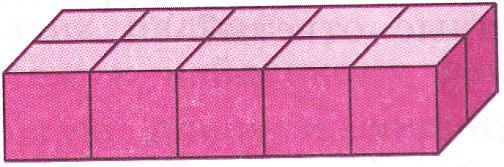 $c:\users\елена\appdata\local\microsoft\windows\temporary internet files\content.word\img.tif$

3) Проверьте свой ответ по чертежу.

4) Как вы думаете, сколько кубиков с ребром 1 см поместится в коробке, высота которой в 3 раза больше коробки, о которой говорится в пункте 2? $c:\users\елена\appdata\local\microsoft\windows\temporary internet files\content.word\img.tif$

Каким способом вы вычислили объём коробки?

Как преобразовали формулу нахождения объёма прямоугольной призмы

Запишите новую формулу нахождения объёма прямоугольной призмы.

V = S_осн.· h

Кто сможет сформулировать тему урока?

(Решение задач на нахождение объёма прямоугольной призмы по площади основания и высоте бокового ребра)

5. Первичное закрепление во внешней речи.

1. Устное решение задач.

S	h	V
6см²	?	18 см³

Составьте обратные задачи.

Если площадь основания 6см² , какой длины могут быть стороны прямоугольного основания?

2. Решение задачи из учебника «Математика», 4 класс, 2 часть, авторы И.И. Аргинская, Е.И. Ивановская, С.Н. Кормишина: № 344(3)

6. Самостоятельная работа с самопроверкой по эталону.

Тест.

1. Прямоугольная призма имеет:

о) 12 граней

п) 8 граней

р) 6 граней

2. Определи объём прямоугольной призмы, если, а=3см, в=2см, h=1 см

у) 3·2+1

ф) (3+2) ·1

х) 3·2·1

3. Определи объём прямоугольной призмы, если,

S_осн.= 4см^2, h= 2см

л) 4 : 2· 2

м)4 · 2

н) 4 · 2 · 2

4. Заполни пропуск 1дм³ = … см³

д) 1000 см³

и)100 см³

й)10.000 см³

Буквы - ответы теста запишите в таблицу.

Какие вопросы оказались трудными?

Отгадайте имя выдающегося ученого Древней Греции по согласным буквам теста.

7. Включение в систему знаний и повторение.

В учебнике, на стр.38 прочитайте текст и скажите, какой закон был открыт Архимедом. Пометьте карандашом, какие знания вам были известны, а какие вы сейчас узнали.

Озвучьте закон, открытый Архимедом.

Какое слово он при этом произнес? Кто знает значение этого слова? Кто сегодня на уроке испытал подобное чувство?

Работа в группах.

Пользуясь законом, открытым Архимедом, попробуйте решить задачи на стр.39

8. Рефлексия деятельности (итог урока).

Чтобы достигнуть последней цели нашего урока нам предстоит продемонстрировать наши знания на практике.
Перед вами лист с заданиями с 3 уровнями сложности. Выберите себе задание, с которым вы справитесь или которое вы бы хотели сделать.

I уровень
Рёбра куба равны 4 см. Определи площадь его основания и объём.

II уровень.
Длина основания прямоугольной призмы 6 дм, а ширина в 2 раза короче. Её боковое ребро равно 7 см. Найди объём прямоугольной призмы .

III уровень.
Объём прямоугольной призмы 56 см³, длина бокового ребра 7 см. Какой длины могут быть стороны основания прямоугольной призмы? Найди все решения.

- Какое открытие вы сделали на уроке?
- Назовите цель нашего урока.
- Какое задание было для вас самым интересным?
-Самым трудным?
Какие трудности остались?
Посмотрите на свои карты достижений оцените свою работу на уроке при помощи уровней.