|
«Решение систем линейных неравенств»
                             Технологическая карта урока Технологическая карта урока
Авторы
|
Кадочникова Татьяна Витальевна
|
Предмет
|
Математика
|
Класс
|
6,8 класс
|
Тема урока
|
«Решение систем линейных неравенств»
|
Тип урока
|
комбинированный
|
Время
|
40 минут
|
Образовательные ресурсы
|
Интерактивная доска, раздаточный материал, презентация
|
Цели урока
|
Цель урока:
повторить решение линейных неравенств; ознакомить с алгоритмом решения систем линейных неравенств; сформировать умение решать системы линейных неравенств любой сложности.
Задачи:
Обучающие
повторить понятия: «линейное неравенство», «система неравенств», «решение системы неравенств», «числовые промежутки», «числовой отрезок, интервал, полуинтервал».
Расширить, обобщить и систематизировать знания о линейных неравенствах и системах линейных неравенств;
Применять свойства неравенств в процессе выполнения заданий;
Повторить алгоритм решения неравенства с одной переменной;
Совершенствовать умения решать неравенства, графически изображать множество их решений, а также записывать решения в виде числового промежутка.
Сформировать умение:
решать системы линейных неравенств, графически изображать множество их решений, а также записывать решения в виде двойного неравенства и в виде числовых промежутков;
находить все целые числа, являющиеся решением системы неравенств;
находить наибольшее/наименьшее целое решение системы неравенств;
наблюдать, анализировать, делать выводы, осмысливать и обобщать учебный материал;
объективно оценивать свою деятельность и деятельность других;
закреплять и повторять ранее пройденный материал.
Развивающие:
развивать логическое мышление при установлении связи графического изображения множества решений системы линейных неравенств, и записи решения с помощью числового промежутка;
развивать навыки самостоятельной работы;
развивать монологическую речь при выполнении заданий;
развивать умение выделять главное;
обобщать имеющиеся знания;
способствовать развитию интереса к предмету, организованности, ответственности
развивать умение выделять главное и обобщать имеющиеся знания;
способствовать развитию интереса к предмету, организованности, ответственности
Воспитательные:
Воспитывать сознательное отношение к учению;
Воспитывать познавательную активность учащихся;
Воспитывать чувство личной ответственности в коллективной работе;
Воспитывать творческую, всесторонне-развитую личность.
|
Формы и методы обучения
|
практический,
наглядный,
словесный.
|
Основные понятия и термины
|
«линейное неравенство», «система неравенств», «решение системы неравенств», «числовые промежутки», «числовой отрезок, интервал, полуинтервал»,
|
Ожидаемые результаты
|
К концу урока учащиеся должны:
уметь решать линейные неравенства и системы;
графически изображать множество их решений, а также записывать решения в виде числового промежутка;
производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение).
|
Организационная структура урока
Этап урока
|
Деятельность учителя
|
Деятельность учащегося
|
Универсальные действия
|
1. Самоопределение к деятельности
|
Организационный момент
|
Включение в деловой ритм
|
Регулятивные: готовить себя к продуктивной деятельности.
|
2. Постановка цели и задачи урока.
|
Устная работа с классом:
Назовите и запишите промежутки, изображённые на рисунке (слайд 1)
Является ли решением неравенства 3х - 11>1 число 5? Дайте определение решения неравенства с одной переменной. Что значит решить неравенство?
Сформулируйте свойства равносильности, которые используются при решении неравенств. Прокомментируйте решение данного неравенства. (слайд 2)
Используя свойства, решите следующие неравенства (работа в тетрадях и у доски):
Тест
(самостоятельная работа, с последующей взаимопроверкой).
Заполнить таблицу:
На каком рисунке изображено множество решений системы 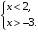
А. Б. В.
2 - 3 - 3 2 - 3 2
Запишите обозначение промежутка :
- 10 5
А. (-10; - 5) Б. 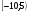 В. В. 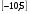
Решите неравенство 2 – 5х < 0.
А. (0,4; + ∞) Б. [0,4; + ∞) В. (- ∞; 0,4)
При каких значениях параметра а двучлен 12 – а принимает положительные значения?
А. а > 12 Б. а > - 12 В. а < 12
При каких значениях у дробь 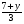 меньше дроби меньше дроби 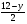 ? ?
А. (- ∞; 4,4) Б. (- ∞; - 4,4) В. (4,4; + ∞)
Найдите наибольшее целое решение неравенства 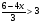
А. – 2 Б. 0 В. – 1
Промежутку [- 2,5; 2,4] принадлежит число …
А. – 2,6 Б. 0 В. 3
Для любых значений х верно неравенство:
А. (х – 2)2 < 0 Б. (х + 3)2 > 0
В. (х + 3)2 > 0 Г. х2 – 10х + 25 ≥ 0
Ответы выводятся на доску (слайд 5).
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
В
|
В
|
А
|
В
|
А
|
В
|
Б
|
Г
|
Сосед по парте проверяет правильность решения и выставляет свою оценку.
Что называют системой неравенств?
Что называют решением системы неравенств?
Что значит решить систему неравенств?
(слайд 4, 5)
Используя числовую ось, найдите пересечение промежутков:
А. 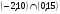 Б. Б. 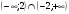 В. В. 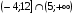
|
Взаимодействуют с учителем во время опроса, осуществляемого во фронтальном режиме
|
Познавательные: умение структурировать информацию, переводить графическую информацию в лингвистическую, понимать на слух ответы учащихся;
Регулятивные: Актуальный контроль на уровне произволь�ного внимания.
Регулятивные: контроль, оценка, коррекция; обнаруживать отклонения и отличия от эталона;
Коммуникативные: осуществлять взаимоконтроль;
адекватно воспринимать оценку учителя.
Познавательные: осознанно и произвольно строить речевое высказывание в устной форме, осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач
|
3. Осмысление нового
|
Давайте рассмотрим решение данной системы неравенств (слайд 6,7,8)
При решении систем неравенств мы будем использовать следующий алгоритм:
Решить каждое из неравенств системы;
Изобразить множество решений каждого неравенства на числовой оси;
Найти на числовой оси пересечение промежутков (если оно есть) и записать его с помощью неравенства или обозначения промежутка (или сделать вывод об отсутствии решения системы).
Вместе разбираем примеры решения систем неравенств с одним неизвестным и отрабатываем запись конкретных решений системы.
Решите систему неравенств:
А. 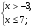
Б. 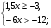
В. 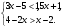
Найти наименьшее целое решение системы неравенств:
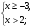  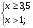 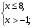
Найти наибольшее целое решение системы неравенств:
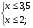 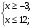 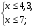
|
В ходе заслушивания ответов одноклассников остальные школьники контролируют правильность и полноту проведенной обработки информации.
По мере необходимости исправляют, дополняют, уточняют.
|
Познавательные: самостоятельное выделение- осознанное формулирование нового знания; умение структурировать информацию, переводить графическую информацию в лингвистическую, понимать на слух информацию;
|
4. Применение знаний (практическая работа).
|
Обучающая самостоятельная работа.
Учащиеся работают самостоятельно, с последующей проверкой и обсуждением.
Необходимо обратить отдельное внимание на дополнительный вопрос в первых двух системах: указать целые решения системы (слайды 9,10)
|
Участвуют в решении задачи. Оценивают качество выполнения задания
|
Познавательные: принимать и сохранять учебную цель и задачу.
Регулятивные: обнаруживать отклонения и
отличия от эталона.
Коммуникативные: адекватно оценивать результаты деятельности одноклассника, корректно поправлять при неправильном ответе; осуществлять взаимоконтроль.
|
5. Подведение итогов.
|
Целью нашего урока было повторение темы «Решение линейных неравенств», и знакомство и первичное закрепление алгоритма решения систем линейных неравенств. Мы научились решать системы неравенств, находить их целые решения, находить наибольшее/наименьшее целое решение системы неравенств.
Домашнее задание:
№ 135,136
Подумайте, и сделайте выводы.
как решить систему трех линейных неравенств:
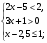
как решить двойное неравенство:
-3,4≤ 2х +5≤ 1,1
|
Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты.
|
| |
|
|
 Скачать 86.66 Kb.
Скачать 86.66 Kb.
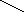
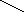
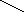
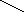
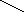
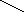
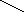
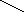
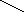









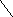
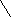
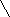



 Технологическая карта урока
Технологическая карта урока