Разноуровневый дифференцированный подход при реализации содержания урока как условие формирования у обучающихся самостоятельности и инициативы Мосолова Надежда Александровна
 Скачать 174.55 Kb. Скачать 174.55 Kb. |
| Разноуровневый дифференцированный подход при реализации содержания урока как условие формирования у обучающихся самостоятельности и инициативы Мосолова Надежда Александровна «Сделать учебную работу насколько возможно интересной для ребенка и не превратить этой работы в забаву – это одни из труднейших и важнейших задач дидактики» К.Д. Ушинский К сожалению, многие люди считают, что математика – «сухая» наука в ней нет ничего интересного; одни только цифры и формулы. Воспитать человека математически образованного, причем гуманными методами в гуманных формах – тот идеал, к которому стремится каждый цивилизованный учитель математики. Гуманизация обучения означает, прежде всего, необходимость его дифференциации, но дифференциация имеет две разновидности: уровневую и профильную. В дифференцированном обучении математике гуманна только одна концепция – концепция единства уровневой и профильной дифференциации. Любая из этих двух разновидностей дифференциации без другой неполноценна. Лишить ученика возможности в полной мере использовать тот или иной вид дифференциации – значит совершить антигуманный акт. Получать удовольствие от занятия математикой школьник может лишь при условии, если дифференциация и индивидуализация будут доступны ему в той степени, в какой он только пожелает. В противном случае один ученик будет учиться налегке, не напрягаясь, а другой – пытаться осилить непосильное. Первый из них не найдет применения имеющимся способностям и не разовьет потенциальные, второй будет чувствовать постоянное унижение, на каждом шагу ощущать собственную неполноценность, умственную убогость, что поведет к отвращению от математики. Профильная дифференциация является важнейшим средством осуществления уровневой дифференциации. Не использовать первую как рычаг для приведения в действие всех возможностей второй – значит заранее запланировать заниженную эффективность обучения по сравнению с той, какой она могла бы быть. Профильная дифференциация означает углубленное изучение математики, расширенное представление о возможностях её приложений в различных областях человеческой деятельности, что означает одновременно и другой уровень обучения математике. Поэтому профильная дифференциация является эффективным средством варьирования уровней обучения предмету, и независимо от того, ведется ли преподавание математики в математическом, гуманитарном, техническом, естественно – биологическом или обычном классе, без профильной дифференциации невозможна эффективная уровневая дифференциация. Поэтому я считаю, что ученику должна быть предоставлена возможность выбора той или иной дифференциации в любое время, в любом классе, в любое время года. Негуманно заявлять ученику, что он опоздал со своим выбором, что надо было сделать это раньше, а теперь уже «поезд ушел» и винить некого, кроме самого себя. Можно сказать и сильнее: на каждом уроке, по каждому из предметов ученику должна быть предоставлена возможность постоянно выбирать собственную, индивидуальную дифференциацию, всё обучение должно состоять в таком непрерывном выборе. Дифференциация должна быть добровольной как для ученика, так и для учителя. Этого требует, прежде всего, принцип гуманных отношений между учителем и учащимся. Без соблюдения указанного требования добровольности гуманные отношения в классе невозможны. Основной целью своей работы я считаю организовать учебный процесс на основе учета индивидуальных особенностей личности, обеспечить качественное усвоение учениками содержания образования, то есть обеспечить каждому ученику условия для максимального развития его способностей, удовлетворения познавательных потребностей и интересов в процессе усвоения им содержания математики. Уже несколько лет в своей работе я применяю систему разноуровневых дифференцированных приемов и методов, позволяющих учащимся овладеть навыками самостоятельной работы, повышающую их познавательную активность, дающую возможность более объективно оценить знания учащихся. Принципиальное отличие дифференцированного метода состоит в том, что перед разными категориями учащихся я ставлю различные цели: одни ученики должны достичь базового уровня подготовки, а другие, проявляющие интерес к математике и обладающие хорошими математическими способностями, должны добиться более высоких результатов. В соответствии с этим в каждом классе я выделяю две группы учащихся: группа базового уровня и группа повышенного уровня. Конечно, состав групп не должен быть застывшим. Любой ученик из группы базового уровня может перейти в группу повышенного уровня, если он хорошо усвоил материал и будет свободно выполнять задания, соответствующим обязательным результатам обучения. С другой стороны, ученик из группы повышенного уровня, если он имеет пробелы в знаниях или не справляется с темпом продвижения группы. Для этого я использую уроки нескольких видов: лекции, практические занятия, семинары, консультации, зачетные уроки. Не буду подробно останавливаться на методике проведения различных видов уроков, скажу лишь несколько слов о формах организации учебно–познавательной деятельности учащихся на них. Дифференцированный подход целесообразно осуществлять на определенных этапах урока.
1 вариант рассчитан на задания, которые соответствуют базовому уровню. П вариант – задания основного задачного материала, но требующие установления связей между отдельными компонентами курса. Ш вариант – задания повышенного уровня, где требуется применение нестандартных приёмов решения.
Конечно, подобное деление в значительной степени условны, однако они удобны, так как при систематическом применении учащиеся уже по названию вида урока заранее знают, как будет на нём организована деятельность их и моя, и оказываются психологически подготовлены к работе. Для себя считаю обязательным сообщать учащимся план работы, начиная большую тему, количество уроков по ней, краткое содержание, какие виды уроков будут применяться при изучении темы, на каких уроках будут проводиться промежуточные зачетные работы, указываю срок итогового зачета по теме. Это я делаю для того, чтобы подготовить учащихся к работе, сделать их активными участниками процесса обучения, стараюсь приучить их к планированию своей деятельности, чтобы они видели конечную цель своей работы. С самого начала изучения темы я знакомлю учащихся с различными уровнями знаний по изучаемой теме. На сегодняшний день это очень легко делается. Для всех выпускных классов, да и не только выпускных, издается огромное количество пособий и дополнительной литературы для подготовки к итоговой аттестации, а именно с различными уровневыми заданиями. Даже в учебниках по алгебре, по алгебре и началам анализа учащиеся хорошо ориентируются по уровневым заданиям. Конечно, есть некоторая условность в определении уровней и подборе соответствующих задач, особенно когда речь идет о заданиях третьего уровня. Есть опасность перегрузки учащихся, использования задач олимпиадного уровня. Ознакомление учащихся с уровнями усвоения материала позволяет им рассчитывать свои силы в ходе изучения темы, они могут самостоятельно и осознанно оценить свои знания и возможности. Не списывать, не обращаться за помощью к родителям и товарищам при первых же неудачах, настойчиво продолжать поиск решения неподдающихся задач – эти качества могут быть свойственны каждому ученику. Но они не могут возникнуть сами по себе. «Воспитание воли, упорства и целеустремленности в любой работе должно составлять главную часть всей воспитательной работы каждого учителя» В.Ф.Шаталов. Одной из проблем нашей гимназии я считаю, является проблема повышения мотивации учащихся: невысокий уровень познавательных интересов учащихся препятствует осознанному выбору дальнейшего направления образования, пути получения профессии. Мотивация – это система побудительных причин человеческого поведения, теоретической и практической деятельности. Такими побудителями могут стать чувства, переживания, идеи, в которых отобразились интересы ребенка, его потребности. Приведу пример, планируя подготовку учащихся 5 класса к восприятию правила умножения десятичных дробей, в начале урока включаю в математический диктант задачу на вычисление площади прямоугольника, длины которого - натуральное число. Решение этой задачи, проверенной и разобранной в ходе проверки математического диктанта, естественно сохраняю на классной доске. Это облегчит формирование мотивации при знакомстве с рассматриваемым правилом. Итак, рассмотрим прямоугольник со сторонами 0,03 дм и 1,08 дм, площадь которого надо найти. Выразим стороны в миллиметрах; отыщем площадь; выразим результат в квадратных дециметрах. Обращаю внимание учащихся на то, что первым шагом была замена десятичных дробей 0,03 и 1,08 натуральными числами 3 и 108, которые получаются, если в данных числах отбросить запятую и не писать нули, стоящие слева от цифры 3. Затем получившие натуральные числа перемножаются. Далее, наконец, отделить в получившемся произведении натуральных чисел, ведя отсчет справа налево, столько же цифр, сколько десятичных знаков в обоих множителях вместе. Очень наглядно это будет видно, если после завершения рассмотренного выше объяснения учащимся показать краткое изложение, заранее подготовленное для кодоскопа: «Чтобы найти произведение десятичных дробей 0,03 х 1,08
3 108=324;
0,03 – 2 знака 1,08 – 2 знака 3) отделяем справа столько знаков, сколько их в обоих множителях: 324 (2 + 2) знака (2 + 2) знака Ответ: 0,03 х 1,08 = 0,0324». На одном из педагогических советов гимназии перед нами – учителями были поставлены задачи по повышению мотивации учащихся: - переориентировать работу учителей с формирования знаний, умений и навыков на обеспечение образования школьников в соответствии с их возможностями, способностями и интересами, опираясь на личностное ориентирование учащихся; - организовать работу учителей по раскрытию перед учащимися социальной, практической значимости изучаемого материала; - активизировать работу по проблеме мотивации учения. Поэтому мы особое внимание уделяем профильному обучению, т.к. оно является комплексным средством повышения качества, доступности и эффективности общего образования, которое позволяет, используя дифференцированное обучение, более полно учитывать интересы, склонности и способности ребят. Работая в профильных классах и в классах с углубленным изучением математики, я всегда ставлю перед собой основные цели: это в первую очередь использование современных технологий, личностно– ориентированный подход, разноуровневую дифференциацию, проектную деятельность, подготовку к районной олимпиаде по математике. Соответственно из целей вытекают задачи: в первую очередь это формирование математических знаний, математической культуры, развитие логического и пространственного мышления, самостоятельности, поддерживать в учащихся процессы самопознания, создать условия для формирования индивидуальной личности учащегося, содействовать интеллектуальному, духовно–нравственному и физическому развитию учащихся, становлению их неповторимой индивидуальности. Если раньше у нас акцент делался на сплочение общешкольного коллектива, то сейчас мы ставим задачу использовать возможности коллективной творческой деятельности для развития индивидуальности учащихся. В своей работе я отказалась от выставления итоговой отметки, как среднего балла из большего числа текущих отметок. В традиционном подходе к оцениванию знаний, на мой взгляд, есть много недостатков. Старая система оценок, по моему, очень губительна для способного ученика, так как получается, чем способнее ученик, тем меньше ему приходиться прикладывать усилий, тем меньше учитель занимается его развитием, что отрицательно сказывается не только на знании предмета, но и на нравственном воспитании личности. В моей практике итоговая оценка является результатом отметок за тематические зачеты. В течение изучения темы я провожу промежуточные зачетные работы. Промежуточные зачеты помогают выявлять у учащихся пробелы в усвоении знаний на образовательном уровне. Эти работы я составляю из заданий, аналогичные тем, которые были сообщены учащимся в начале изучаемой темы, и соответствуют обязательным результатам обучения. За них отметки не ставлю, они оцениваются лишь «зачтено» или «не зачтено». В конце изучения темы я провожу зачет, в результате которого ученик получает итоговую отметку за тему. Хочется отметить, что доверие к ученику, система работы, которая позволяет ему чувствовать себя не «объектом воспитания и обучения», а полноправным участником учебного процесса с четко очерченным кругом требований, которые ему необходимо выполнить, имеющим возможность самостоятельно планировать свою деятельность выбирать для себя в соответствии со своими возможностями определенный уровень усвоения материала приводит к тому, что ученики не злоупотребляют моим доверием. Когда учащиеся привыкают работать по разноуровневой системе зачетов, довольно резко меняется стимул учения: над ними не висит страх получения плохой оценки, они начинают учиться, прежде всего, потому, что сами этого хотят. Ребята учатся планировать свою деятельность, видеть конечную цель работы, распределять свои силы на достаточно долгий промежуток времени, добиваться поставленной цели. Кроме того, определение истинного уровня знаний каждого ученика, нацеливание их на максимальное использование и развитие собственных способностей не только дает мне реальную картину знаний, но и представляет возможность самому ученику объективно оценивать их. Очень люблю на уроках использовать вербальные оценки, в которых выражаю своё эмоциональное отношение к работе учащихся, например: «Прекрасный ответ», «Очень точный ответ. Тебя было приятно слушать», «Решение задачи этим способом, это высший пилотаж в математике» или «Ты меня очень огорчил этой работой». В своей работе использую задания инвариантные, индивидуальные задания и специальные задания для детей, особо интересующихся математикой. И здесь на первый план выходит работа по подготовке учащихся к олимпиадам, проектная деятельность учащихся, работа с одаренными детьми. Введение в 9 – 11 классах спецкурса и элективных курсов по математике по теме: «Методы решения нестандартных задач» помогает мне в этом. Какие задачи я ставлю перед собой в работе по элективным курсам и спецкурсам в старших классах? - уточнение готовности учащихся и способности осваивать математику на повышенном уровне; - формирование у учащихся интереса к выбранному предмету; - создание условий для подготовки учащихся к математическим олимпиадам, к успешной сдачи ЕГЭ. В связи с этим основные темы этих курсов состояли в: ● углублении отдельных базовых общешкольных тем; ● расширении некоторых тем, выходящих за их рамки; ● практикумы по решению познавательных задач повышенной сложности; ● прикладное применение некоторых базовых тем; ● проектно – исследовательская деятельность учащихся. Основные требования к элективным курсам это: √ избыточность (обеспечивает реализацию запросов учащихся); √ оригинальность содержания (направлена на развитие мотивации учащихся на профильное обучение); √ обеспечивает практическую и творческую направленность курса. Сравнительный анализ качества знаний учащихся профильных математических классов с 2005-2006 уч. г. по 2007-2008 уч. г.
Многие учащиеся повысили свои годовые отметки, около 98 % учащихся подтверждают свои отметки на итоговых аттестациях и около 9 % повышают их, так на итоговой аттестации в 11 классе по результатам ЕГЭ 94 % учащихся сдали экзамен по математике на «4» и «5». По результатам исследований и анализа различных видов мониторингов учащиеся профильных математических классов всегда имеют выше процент качества знаний (до 92%) и процент обученности (до 77 %). Сравнительный анализ результатов входящих мониторингов, проводимых в сентябре каждого учебного года, показал позитивную динамику учебных достижений моих учащихся, ниже показан рост процента качества знаний: - учащихся профильного математического класса: 2005 год – 9 «Б» класс – 81 % качество, 72 % обученность 2007 год - 11 «Б» класс – 84 % качество, 74 % обученность Сравнительный анализ результатов учащиеся профильного математического класса 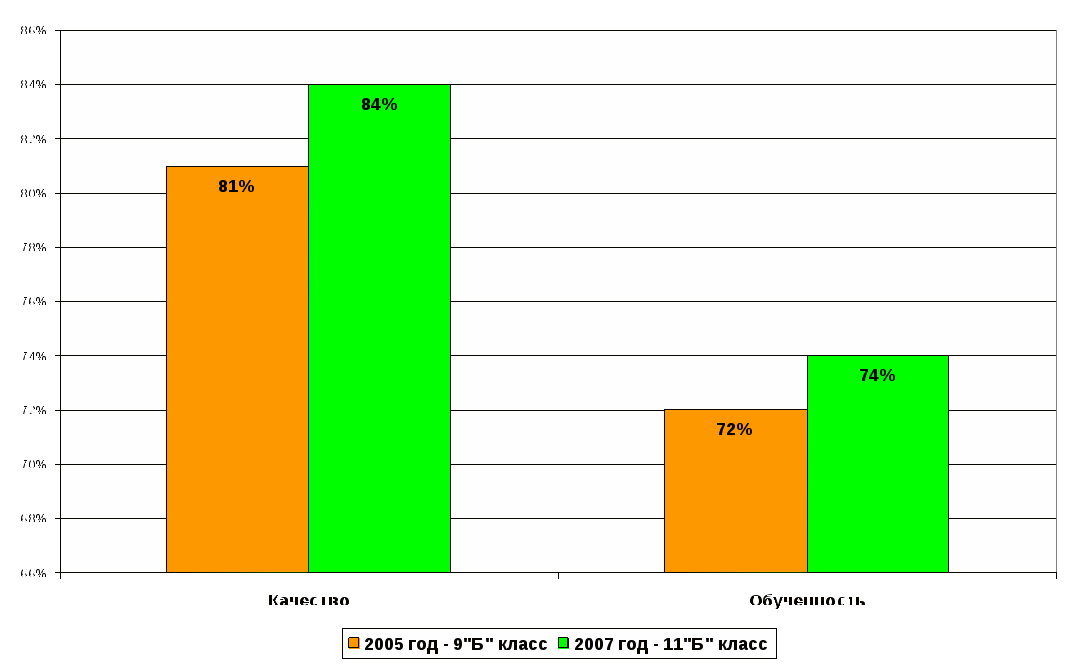 - учащиеся гуманитарных классов: 2005 год - 9 «А» класс – 68 % качество, 68 % обученность 2005 год 7 « В» класс – 57 % качество, 54 % обученность 2007 год – 11 «А» класс – 65 % качество, 69 % обученность 2007 год - 9 « В » класс – 58 % качество, 56 % обученность. В процессе своей работы я увидела, что в классе, в целом, повысился уровень знаний, умений и навыков учащихся; возрос интерес школьников к математике, повысились способности учеников к глубокому изучению программного материала, то есть можно заключить, что эффективность обучения повысится, если будет использоваться дифференцированное обучение. Сравнительный анализ результатов учащиеся гуманитарных классов 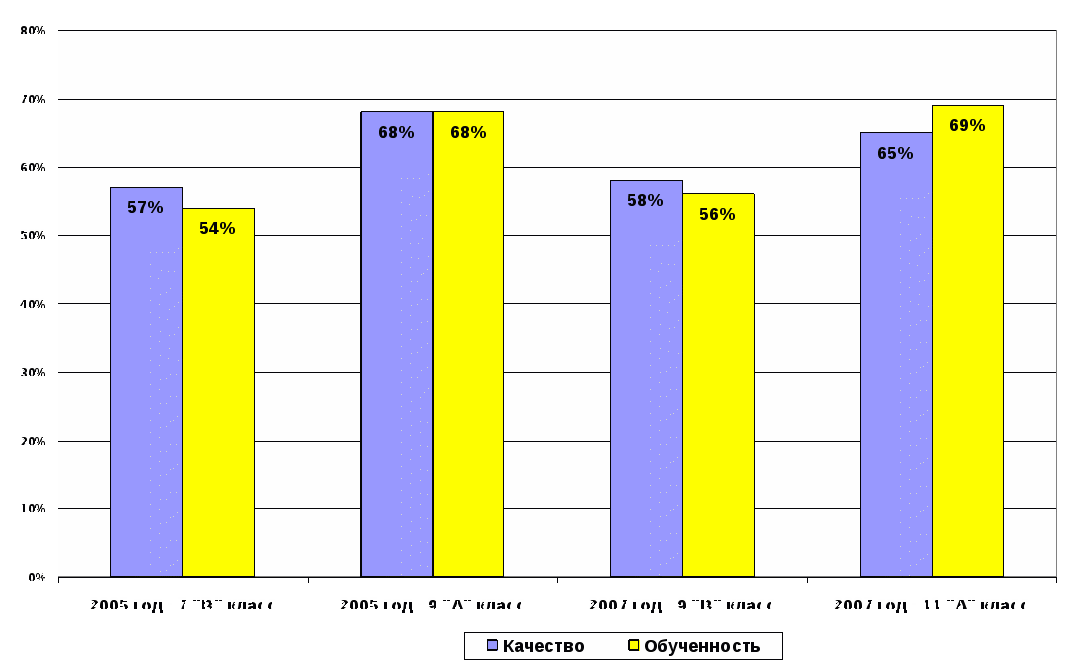 Добиваясь личной мотивации познавательной активности по математике у учащихся, позволяет мне умело диагностировать индивидуальный уровень развития каждого ученика и ставить определенные целевые установки для каждого ученика, поэтому при подготовке к каждому уроку, к каждому внеклассному мероприятию я четко для себя формулирую цель и задачи, стараюсь превратить учебный организационный момент на уроке в организационно – психологический момент, задающий деятельную тональность всему уроку. Мои ученики каждый год принимают активное участие в математических олимпиадах разного уровня, здесь и международная олимпиада «Кенгуру – математика для всех» и показывают неплохие результаты: с 2005 – 2008 годы в различных олимпиадах приняли участие 198 человек. Из них 11 человек заняли I и II места в районных олимпиадах по математике, в международной олимпиаде «Кенгуру»: * в 2005 году Плец Ольга заняла II место в районной олимпиаде по математике; * в 2006 году Плец Ольга заняла I место, Цуркан Макар - II место в районной олимпиаде по математике; * в 2007 году Плец Ольга и Цуркан Макар заняли II место, Купашев Юрий - III место в районной олимпиаде по математике; * в 2008 году Медведев Виталий - I место, Капцов Михаил - II место в районной олимпиаде по математике. Для подготовки учащихся к олимпиадам, конкурсам не один год я веду спецкурсы, кружки и элективные курсы по математике «Решение нестандартных задач, задач повышенной трудности», «Решение задач с параметрами». Большое внимание уделяю методике психологической поддержке и предметной подготовке учащихся к Единому Государственному Экзамену. Очень важно настроить учащегося на позитивное отношение к работе, приучить работать в предмете продолжительное время. Знакомлю учащихся с некоторыми методиками и различными правилами подготовке к ЕГЭ . Проектная деятельность учащихся – одно из направлений личностно – ориентированного обучения, поэтому и задача, которая ставиться передо мной - это выявление избирательности ученика к содержанию, виду, форме учебного материала, процессу самореализации и виду деятельности. Для каждого ученика я выявляю три основные линии развития:
Метод проектов – педагогическая технология, цель которой – ориентировать на интеграцию фактических знаний (порой и путем самообразования) для активного включения в освоение новых способов человеческой деятельности. Учебный проект – это задание учащимся, сформулированное в виде проблемы, и их целенаправленная деятельность, форма организации взаимодействия учащихся с учителем и учащихся между собой и результат деятельности как найденный ими способ решения проблемы проекта. Проектная деятельность формирует личностные качества учащихся, в первую очередь – умение работать в коллективе. Брать на себя и разделять ответственность за выбор, решение вопросов, анализировать результаты деятельности. И на этом этапе презентации, я учу учащихся кратко излагать свои мысли, логически связно выстраивать сообщение, изготавливать наглядность, вырабатывать стройную манеру изложения, поэтому и моя роль, как учителя, значительно возрастает. Важно, чтобы учебный и воспитательный эффекты были максимальными. Работая над проектами с 2002 года, отмечу, что у учащихся возросло желание самостоятельно, творчески делать небольшие открытия для себя, ребятам нравиться исследовательская работа. Некоторые темы проектов с 2003 года: Общешкольный проект «Откуда есть, пошла Земля Русская» 1. Математика в древней Руси. Старинные задачи – шутки. 2. «Цифры, счет, система записей у славян» 3. Решение задач методом уравнений (по теме: «Государевы регалии») 4. Математические кроссворды по теме: «Древняя Русь». 5. История Москвы в задачах по математике. 6. Старинные русские меры измерения. Общешкольный проект «Во славу русского воинства» 7. Практическое применение математики в военных действиях. Общешкольный проект « … Так может собственных Платонов российская земля рождать» 8. Великие математики 17 – 18 века: «О Леонтии Филипповиче Магницком, Николае Ивановиче Лобачевском, Григории Григорьевиче Скорнякове – Писареве, Павле Степановиче Щепкине, Тимофее Федотовиче Осиповском и т.д.» 9. Выдающаяся дочь России. 10 Н.И.Лобачевский и открытие неевклидовой геометрии. 11. Тела Платона. Правильные многогранники. 12. О теореме Пифагора и способах её доказательства. 13. Пифагор и его знаменитая теорема. 14. Математика и музыка (в тональности ми мажор). 15. К вопросу о математической гармонии в музыке или проверить алгеброй гармонию. «Не существует сколько–нибудь достоверных тестов на одаренность, кроме тех, которые проявляются в результате активного участия хотя бы в самой маленькой поисковой исследовательской работе » А. Н. Колмогоров.  Начиная с 2006 года за подготовку учащихся к олимпиадам, меня награждают грамотами Управления образовния Ленинского района, имею Благодарность Главы Ленинского муниципального района Московской области. Два года подряд, т.е. в 2007 и 2008 годах мои учащиеся награждаются премией Главы Ленинского муниципального района: ПЛЕЦ ОЛЬГА, ЦУР КАН МАКАР(2007 год и 2008 год), ПАРШИНА АНАСТАСИЯ (2008 год). Огромной радостью для меня стали результаты поступления моих ребят в престижные Вузы г. Москвы. Плец Ольга и Цуркан Макар поступили на бюджетное отделение в Государственный университет - Высшей школы экономики, Купашев Юрий, Зайцев Станислав и Янес Андрей в Московский Государственный технический университет им. Н.Э. Баумана, Кулакова Анна и Паршина Анастасия в Российскую экономическую академию им. Плеханова и т.д. Среди моих выпускников 2008 года девять человек получили золотые и серебряные медали, четыре из них учащиеся моего 11 «Б» класса, где я семь лет была классным руководителем. В 2007 году ученица моего 10 «Б» класса Нестерова Анна, участвуя в конкурсе «ВИДНОВЧАНКА» стала победителем этого конкурса. В 2008 году Плец Ольга и Цуркан Макар стали финалистами районного конкурса « ИКЕЯ – ВУЗ». Смысл всей своей работы в школе я могу выразить стихами Н. Комисаренко: ПОМОЖЕМ НАШИМ ДЕТЯМ Душа болит за наше поколенье, Что в спячку в основном погружено. Нет творческих полетов и горенья, Рутина, фальшь, бездействие, вино. И мрак покрыл образованье: Духовности в помине нет, И в школах истинных нет знаний, Дается мертвым языком предмет. Детей всех учат « под одну гребенку», Стремятся информацией снабдить, Перегружают бедного ребенка. А ему лишь надо научиться ЖИТЬ! Его должны мы подготовить к пониманью Всей жизни смысла наперед, Что все едино в этом мирозданье, И по одним законам все живёт. Наполнить жизнь его добром и красотой, Раскрыть и углубить его сознанье, Он в жизнь приходит не пустой – С потенциалом скрытых знаний. Их прошлых жизней он несет с собой Способности, возможности, таланты. И мы должны с любовью, добротой Помочь раскрыть, отшлифовать брильянты. |