|
Рабочая программа по алгебре для 9а класса Зубенко Надежды Александровны 2012 год Пояснительная записка
Муниципальное бюджетное образовательное учреждение
Уршельская средняя общеобразовательная школа
Принята Утверждена
на заседании МО Приказом директора школы
учителей математики №203а от 30.08.2012 г.
29 августа 2012 г.
Руководитель МО:__________Грачёва В.В. Директор школы:__________Мудрецов Ю.А.
Рабочая программа
по алгебре для 9а класса
Зубенко Надежды Александровны
2012 год
Пояснительная записка
Рабочая программа по алгебре для 9 класса основной общеобразовательной школы составлена на основе
федерального компонента Государственного стандарта основного общего образования по математике (Стандарт основного общего образования по математике //Математика в школе. – 2004г., №4),
программы общеобразовательных учреждений «Алгебра 7-9 классы», составитель Т.А. Бурмистрова, (Москва: «Просвещение», 2009),
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2011-12 учебный год
инструктивно-методического письма «О преподавании учебного предмета Математика» в образовательных учреждениях Ярославской области в 2011/2012 уч. г.»
Данная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Программа соответствует учебнику «Алгебра» для девятого класса образовательных учреждений /Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, Москва: «Просвещение», 2009год, дидактические материалы по алгебре для 9 класса /Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова, М.: Просвещение, 2010 год.
Преподавание ведется по первому варианту – 3 часа в неделю, всего 102 часа. В программе может произойти изменение количества часов по темам из-за проведения диагностических и тренировочных работ в формате ГИА в системе СтатГрад. Планируется проведение трех диагностических и четырех тренировочных работ. Возможны расхождения в количестве часов на изучение отдельных тем и количеством самостоятельных работ. Уменьшено на 1ч количество часов на изучение тем: «Элементы комбинаторики и теории вероятностей» и «Повторение» из-за отсутствия вводного повторения в начале 9 класса в авторской программе.
Основными средствами контроля являются тематические контрольные работы. Предусматривается проведение 8 контрольных работ, одна из них – итоговая.
Цели изучения:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся овладевают приёмами вычислений на калькуляторе.
Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышле�ния, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Требования к уровню подготовки учащихся
В результате изучения курса алгебры 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к 0, у=кх+b, у=х2, у=х3, у = 0, у=кх+b, у=х2, у=х3, у =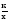 , у= , у= , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики; , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, комбинаторики, статистики и теории
вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Учебно-тематический план
Номер урока
|
Название темы
|
Количество часов
|
Требования к уровню подготовки учащихся
|
Квадратичная функция. 19 ч.
|
Знать/понимать:
- понятие функции, области определения, области значений;
- свойства функций;
- определение квадратного трехчлена, корни квадратного трехчлена, способ разложения на множители;
- понятие квадратичной функции, ее свойства и способы построения графика;
- квадратное неравенство и способы его решения.
Уметь:
- находить область определения и множество значений для функций, заданных формулой и графически;
- находить корни квадратного трехчлена и выполнять разложение на множители;
- строить и читать график квадратичной функции;
- решать квадратные неравенства, используя графические представления.
|
1-3
|
Функции и их свойства.
|
3
|
4-5
|
Свойства функций.
|
2
|
6-7
|
Квадратичный трехчлен и его корни.
|
2
|
8-9
|
Разложение квадратного трёхчлена на множители.
|
2
|
10
|
Разложение квадратного трёхчлена на множители. Самостоятельная работа.
|
1
|
11-12
|
Функция y=ax², её график и свойства.
|
2
|
13-14
|
Графики функций y=ах²+n и y=а(х-m)².
|
2
|
15-18
|
Построение графика квадратичной функции.
|
4
|
19
|
Контрольная работа №1 по теме «Квадратичная функция»
|
1
|
Степенная функция. 7 ч.
|
Знать/понимать:
- определение четной и нечетной функций,
- свойства степенной функции;
- определение корня n-ой степени;
- свойства корня n-ой степени.
Уметь:
- распознавать четные/нечетные функции по графику;
- описывать свойства степенных функций на основе их графического представления;
- находить значение корня n-ой степени;
- применять свойства корня n-ой для преобразования выражений.
|
20-21
|
Степенная функция.
|
2
|
22-23
|
Корень n-степени.
|
2
|
24-25
|
Степень с рациональным показателем.
|
2
|
26
|
Контрольная работа №2 по теме «Степенная функция»
|
1
|
Уравнения и неравенства с одной переменной. 17 ч.
|
Знать/понимать:
- целое уравнение, биквадратное уравнение;
- способы решения уравнений;
- метод решения уравнений путем замены переменной;
- методы решения систем уравнений и задач с помощью систем уравнений.
Уметь:
- решать уравнения, сводящиеся к квадратным;
- решать системы двух уравнений, одно из которых линейное, а другое – второй степени;
- решать задачи с помощью систем уравнений.
|
27-29
|
Целое уравнение и его корни.
|
3
|
30
|
Целое уравнение и его корни. Самостоятельная работа.
|
1
|
31-34
|
Дробно-рациональные уравнения.
|
4
|
35
|
Контрольная работа №3 по теме «Уравнения с одной переменной»
|
1
|
36-38
|
Решение неравенств с одной переменной.
|
3
|
39
|
Решение неравенств с одной переменной. Самостоятельная работа.
|
1
|
40-42
|
Решение неравенств методом интервалов.
|
3
|
43
|
Контрольная работа №4 по теме «Неравенства с одной переменной»
|
1
|
Уравнения и неравенства с двумя переменными 16 ч.
|
44-45
|
Уравнение с двумя переменными и его график.
|
2
|
46-47
|
Графический способ решения систем уравнений.
|
2
|
48-50
|
Решение систем уравнений второй степени.
|
3
|
51
|
Решение систем уравнений второй степени. Самостоятельная работа.
|
1
|
52-54
|
Решение задач с помощью систем уравнений второй степени.
|
3
|
55
|
Решение задач с помощью систем уравнений второй степени. Самостоятельная работа.
|
1
|
56
|
Неравенства с двумя переменными.
|
1
|
57-58
|
Системы неравенств с двумя переменными.
|
2
|
59
|
Контрольная работа №5 по теме «Уравнения и неравенства с двумя переменными»
|
1
|
Арифметическая и геометрическая прогрессии. 15 ч.
|
Знать/понимать:
- о способах задания числовой последовательности;
- определения арифметической и геометрической прогрессий;
- формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии;
- формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии.
Уметь:
- задавать числовую последовательность аналитически, словесно, рекуррентно;
- привести примеры числовых последовательностей;
- применять формулы при решении задач.
|
60
|
Последовательности.
|
1
|
61-63
|
Определение арифметической прогрессии. Формула n-члена арифметической прогрессии.
|
3
|
64-66
|
Формула суммы первых n-членов арифметической прогрессии.
|
3
|
67
|
Контрольная работа №6 по теме «Арифметическая прогрессия»
|
1
|
68-70
|
Определение геометрической прогрессии. Формула n-члена геометрической прогрессии.
|
3
|
71-73
|
Формула суммы первых n-членов геометрической прогрессии.
|
3
|
74
|
Контрольная работа №7 по теме «Геометрическая прогрессия»
|
1
|
Элементы комбинаторики и теории вероятностей. 14 ч.
|
Знать/понимать:
- о всевозможных комбинациях, о комбинаторных задачах, о дереве возможных вариантов;
- как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения.
Уметь:
- решать несложные комбинаторные задачи.
|
75-76
|
Примеры комбинаторных задач.
|
2
|
77-78
|
Перестановки.
|
2
|
79-80
|
Размещения .
|
2
|
81-82
|
Сочетания.
|
2
|
83
|
Самостоятельная работа.
|
1
|
84-85
|
Относительная частота случайного события.
|
2
|
86-87
|
Вероятность равновозможных событий.
|
2
|
88
|
Контрольная работа №8 по теме «Элементы комбинаторики и теории вероятностей»
|
1
|
Повторение. 14 ч.
|
Уметь использовать приобретенные знания и умения в практической деятельности для решения задач разного уровня сложности на основе изученного материала.
|
89-90
|
Решение текстовых задач.
|
2
|
91-92
|
Функции и их графики.
|
2
|
93-94
|
Решение неравенств.
|
2
|
95
|
Решение уравнений, приводимых к квадратным.
|
1
|
96
|
Системы уравнений с двумя переменными.
|
1
|
97
|
Арифметическая прогрессия.
|
1
|
98
|
Геометрическая прорессия.
|
1
|
99
|
Степенная функция.
|
1
|
100
|
Корень n-степени.
|
1
|
101
|
Итоговая контрольная работа.
|
1
|
102
|
Анализ итоговой контрольной работы.
|
1
|
Содержание программы учебного курса
Глава 1. Свойства функций. Квадратичная функция (26 ч)
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Степенная функция.
Основная цель - расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квад�ратного трехчлена, разложении квадратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функций у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Обучающиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида 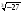 , ,  . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется. . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
Глава 2. Уравнения и неравенства с одной переменной (17 ч)
Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.
Основная цель- систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной. Сформировать умение решать неравенства вида ах2 + bх + с >0 или ах2 + bх + с < 0, где а ≠ 0.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Обучающиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
Расширяются сведения о решении дробных рациональных уравнений. Обучающиеся знакомятся с некоторыми специальными приёмами решения таких уравнений.
Формирование умений решать неравенства вида ах2 + bх + с >0 или ах2 + bх + с < 0, где а ≠ 0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы, её расположение относительно оси ОХ).
Обучающиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
Глава 3. Уравнения и неравенства с двумя переменными. (16 ч)
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Основная цель- выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.
В данной теме завершается изучение систем уравнений с двумя переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный обучающимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.
Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Изучение темы завершается введением понятий неравенства с двумя переменными и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используются при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем.
Глава 4. Прогрессии (15 часов)
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Основная цель -дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
Глава 5. Элементы комбинаторики и теории вероятностей (14 ч)
Комбинаторное правило умножения. Перестановки, размеще�ния, сочетания. Относительная частота и вероятность случайного события.
Основная цель- ознакомить обучающихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний.
При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме обучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
6. Повторение (14 ч)
Основная цель - повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.
Средства контроля:
Переводная аттестация, промежуточный, предупредительный контроль; контрольные работы. Контрольные работы взяты из учебно-методического обеспечения.
Учебно-методическое обеспечение
1) учебник «Алгебра-9» автор Ю.Н. Макарычев, Н.Г. Миндюк, М:Просвещение 2008г.
2)Ковалёва Г.И. Уроки математики в 9-м классе. Поурочные планы.Часть 1 и2.-Волгоград,2002г.
3)дидактические материалы по алгебре 9кл. Автор Ю.Н. Макарычев М:Просвещение 2008г.
4)Тесты по алгебре:9 класс: к учебнику Ю.Н.Макарычева и др. «Алгебра.9 класс»/Ю.А.Глазков, И.К.Варшавский-М:Изд-во «Экзамен»,2011г.
5) Сборник заданий для подготовки к ГИА-9 авт. Л.В. Кузнецова М:Просвещение 2009г.
6)И.В. Ященко, А.В. Семенов «сборник заданий для подготовки к ГИА-9» 2009г. |
|
|
 Скачать 228.35 Kb.
Скачать 228.35 Kb.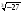 ,
,  . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется. 0, у=кх+b, у=х2, у=х3, у =
0, у=кх+b, у=х2, у=х3, у =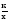 , у=
, у= , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
, у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;