«Решение систем уравнений второй степени» Учитель математики Искабулова С. Х. 2012 2013 уч год Тема урока: «Решение систем уравнений второй степени» Тип урока: урок формирования новых умений
            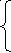 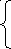  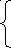 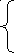        МБОУ « Новоурусовская СОШ» МБОУ « Новоурусовская СОШ»Красноярского района Астраханской области. Урок алгебры в 9 классе по теме « Решение систем уравнений второй степени» Учитель математики Искабулова С.Х. 2012 – 2013 уч.год Тема урока: « Решение систем уравнений второй степени» Тип урока: урок формирования новых умений. Цели: 1) Закрепить умение решать системы уравнений второй степени; Повторить алгоритм решения систем уравнений второй степени. 2) Рассмотреть некоторые нестандартные приёмы решения систем уравнений второй степени с двумя переменными, решение текстовых задач с помощью систем. 3) Способствовать формированию умений обобщать, проводить рассуждения, анализировать. Развивать мышление и речь. Оборудование: компьютер, экран, проектор. Ход урока. 1.Организация класса. Объявление темы, цели урока. 2. Проверка домашнего задания: Решения № 435,б; Сборник Лысенко 2.21 стр 103 на экране. Учащиеся сравнивают результаты пунктов д/р, делают анализ ошибок. Ответы: №432 в)(3; -1); № 435 б) (-3,5; 2,5) и (3,5; -2,5) Л. 2.21: Вычислите координаты точек пересечения парабол у = 3х2 – 8х -2 и у = х2 – 4. Решение: находим решение уравнения 3х2 – 8х -2 = х2 – 4. Х2 -4х+1 =0, х1 = 2+ 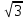 , х2 = 2 - , х2 = 2 - 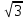 Тогда у1 = 4 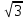 +3; у2 = 3 - 4 +3; у2 = 3 - 4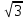 . .Ответ: ( 2+ 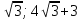 ) и (2 - ) и (2 - 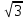 ; 3 - 4 ; 3 - 4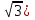 3. Фронтальный опрос (мозговой штурм) :
4. Самостоятельная работа. ( три группы, в каждой группе свой консультант) Задание: указать номер верного ответа (на карточках).
Верные ответы: 1 группа: № 2, 2 группа: № 3, 3 группа: № 1. 5. « Для тех, кто хочет знать больше» Фронтальная работа (15 мин) 1) Решим систему: х2 – 9у2 –х + 3у = 0, Х2 –ху +у =7. Решение: Многочлен из левой части 1-го уравнения разложим на множители: х2 – 9у2 –х + 3у = (х – 3у) (х + 3у) – (х – 3у) = (х – 3у) (х + 3у - 1), тогда получаем равносильную систему: (х – 3у) (х + 3у - 1) = 0, х – 3у = 0, Х2 –ху +у =7. х + 3у – 1 =0; х + 3у – 1 =0, Х2 –ху +у =7. Решим отдельно 1-ую систему: х – 3у = 0, х + 3у – 1 =0; х = 3у, 9у2 -3у2 +у – 7 = 0; Из 2-го уравнения: 6у2 +у -7 = 0 Д = 169, у1 =- 1 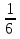 , у2 = 1. , у2 = 1.Тогда х1 =-3 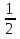 и х2 = 3. Получили пары (-3 и х2 = 3. Получили пары (-3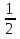 ; -1 ; -1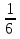 ) и (3; 1). ) и (3; 1).Из второй системы: х = -3у + 1, (-3у + 1)2 – у(-3у + 1) + у – 7 = 0 2у2 - у – 1 = 0 У3 = - 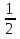 , у4 = 1. Тогда х3= 2,5 и х4 = -2. , у4 = 1. Тогда х3= 2,5 и х4 = -2.Получили пары (2,5 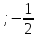 ) и (-2; 1) ) и (-2; 1)Ответ: (-3 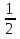 ; -1 ; -1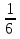 ); (3; 1) и (2,5 ); (3; 1) и (2,5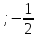 ) и (-2; 1) ) и (-2; 1)2) Решим систему: х2 + 3ху + у2 = 11, Ху + х + у = 5; Решение: уравнения этой системы содержат сумму переменных (х + у), Произведение ху и сумму квадратов (х2 + у2 ). Если в этой системе заменить х на у, а у на х , то получим ту же систему. Такие системы называют симметричными. Их удобно решать, вводя новые переменные. Пусть х + у = u, ху = v , Тогда х2 + у2 = (х +у)2 - 2ху = u2 - 2v. Получаем u2 - 2v + 3v = 11, u2 + v = 11 v + u = 5; v + u = 5; Решив эту систему способом подстановки, найдём, что u1 = -2; v1 = 7; u2 = 3; v2 = 2. Тогда, подставив в замену, получим: Х + у = -2, х + у = 3, Ху = 7; и ху = 2 ; Первая система даёт : х = -2 – у, (-2 - у) у = 7 -у2 – 2у – 7 = 0 Д = - 24 < 0 решений нет. Вторая система: х = 3 – у, у(3 - у) = 2; -у2 + 3у – 2 = 0 Д = 1, у1 = 1, у2 = 2; тогда х1 = 2, х2 = 1. Ответ: (1; 2); (2; 1) Для той группы учащихся, которым такая работа непосильна, можно предложить задачи из учебника № 538 Решение: составим систему: х +у = 5 (х - у), х2 - у2 = 180. ОДЗ: х, у > 0. Ответ: 18 и 12. № 541. Решение: пусть число десятков – х, а число единиц – у, тогда данное число имеет вид 10х + у. Из условия имеем: 4(х +у) = 10х + у, 2ху = 10х + у; Получим х = 3, у = 6, 10* 3 +6 = 36. Ответ: 36 Если позволит время можно «устроить» обмен информацией между этими группами. 6. Из материалов ГИА. 2х + 3у= 4, Задание: При каком р верно решение системы х – у = -3, Х + 2у = р ? Решение: Надо решить систему 2х + 3у= 4, х – у = -3, получим пару (-1; 2) и эту пару подставим в третье уравнение : -1 + 2*2 =р р =3 Ответ: система имеет решение при р =3. По желанию дома решите аналогичное задание: при каком р система имеет решение 3х – 2у = 7, Х + у = 4, 2х – у = р. 7. Итог урока. Выставление оценок. Д/з : №441, № 444(б) + Сборник Лысенко №2.23 |
 Скачать
Скачать
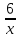 - гипербола I и III четверти.
- гипербола I и III четверти.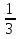 ; 3)
; 3)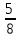 ; -
; - 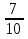 ),
),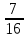 ),
),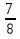 ); (-2; 1)
); (-2; 1)