Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

Протокол № от 2011 г. Руководитель шмо /Т. Е. Терехина



НазваниеПротокол № от 2011 г. Руководитель шмо /Т. Е. Терехина
страница4/5
Дата15.03.2016
Размер0.6 Mb.
ТипПротокол
1   2   3   4   5







БЛОК 8 (ГЕОМЕТРИЯ)




ГЛАВА III.

МНОГОГРАННИКИ
Цель: дать учащимся систематические сведения о перпендикулярности прямых и плоскостей в пространстве, ввести понятие углов между прямыми и плоскостями, между плоскостями
12









§1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА
Знать и понимать:

  • понятие многогранника, основные виды многогранников, изображение многогранников на плоскости;

  • призмы и их элементов, виды призм;

  • формулу для вычисления площади боковой поверхности прямой призмы;

  • формулу для вычисления площади боковой поверхности наклонной призмы;

  • понятие пирамиды, правильной пирамиды, усеченной пирамиды;

  • формулу для вычисления площади полной поверхности пирамиды;

  • свойства пирамид, имеющих равные боковые ребра; равные апофемы;

  • понятие правильного многогранника

Уметь:

  • применять изученную теорию к решению задач;

  • выводить формулы



4






147
Понятие многогранника. Призма (определение, элементы), п. 25-27



1






148
Виды призм. Площадь поверхности прямой призмы, п.27



1






149
Наклонная призма. Площадь поверхности наклонной призмы, п. 27



1






150
Построение сечений призмы



1









§2. ПИРАМИДА



5






151
Пирамида. Площадь полной поверхности пирамиды, п. 28



1






152
Правильная пирамида. Площадь боковой поверхности правильной пирамиды, п. 29



1






153
Ключевые задачи. Свойства пирамид, имеющих равные боковые ребра; равные апофемы, п. 28-29



1






154
Усеченная пирамида. Площадь боковой поверхности усеченной пирамиды, п. 30



1






155
Решение задач по теме: «Пирамида», п.28-30



1









§3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ



2






156
Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников, п. 31-33



1






157
Правильные многогранники, п. 31-33



1






158
Контрольная работа № 4 по теме: «МНОГОГРАННИКИ», п. 25 – 33.
Контрольная работа
1












БЛОК 9 (АЛГЕБРА И НАЧАЛА АНАЛИЗА)




ГЛАВА 7.

ПРОИЗВОДНАЯ
Цель: ознакомить учащихся с методами дифференциального исчисления, научить использовать приобретенные знания и умения в простейших случаях, в практической деятельности и повседневной жизни
35









§37. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Знать и понимать:

  • сходящаяся последовательность, расходящаяся последовательность;

  • окрестность точки, радиус окрестности;

  • сумма бесконечной геометрической прогрессии;

  • предел функции на бесконечности;

  • предел функции в точке;

  • приращение функции, приращение аргумента

Уметь:

  • находить приращение по формулам;

  • определять некоторые пределы последовательностей, предел функции на бесконечности, предел функции в точке.



3






159
Определение числовой последовательности и способы ее задания, п. 1



1






160

161
Свойства числовых последовательностей, п. 2



2












§38. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ



2






162
Определение предела последовательности. Свойства сходящихся последовательностей, п. 1-2



1






163
Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии, п. 3-4



1









§39. ПРЕДЕЛ ФУНКЦИИ



3






164
Предел функции на бесконечности, п. 1



1






165
Предел функции в точке, п. 2



1






166
Приращение аргумента, приращение функции, п. 3



1









§40. ОПРЕДЕЛЕНИЕ ПРИЗВОДНОЙ
Знать и понимать:

  • производная, ее геометрический и физический смысл;

  • дифференцируемая функция;

  • правила дифференцирования,

  • формулы дифференцирования;

  • алгоритм отыскания производной;

  • уравнение касательной к графику функции;

  • таблица производных основных элементарных функций;

  • производная функции вида ;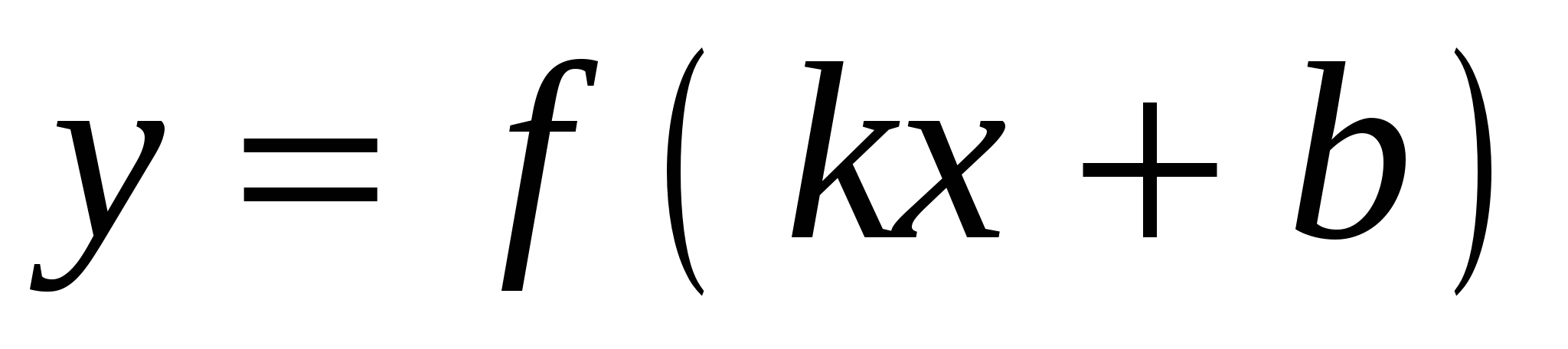

Уметь:

  • вычислять производные элементарных функций, применяя



2






167
Задачи, приводящие к понятию производной, п. 1



1






168
Определение производной, п. 2



1









§41. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ



4






169
Формулы дифференцирования, п.1



1






170

171
Правила дифференцирования, п. 2

  • правила вычисления производных и первообразных, используя справочные материалы;

  • вычислять производную суммы, произведения, частного функций;

  • находить производную сложной функции;

  • находить уравнение касательной, координаты точек касания;

  • уметь написать уравнение касательной к функции в заданной точке;

  • определять угол наклона касательной



2









172
Понятие и вычисление производной n-го порядка, п. 3



1






173

174

175
§42. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ



3












176

177

178
§43. УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ



3












179

180
Контрольная работа № 6 по теме: «ПРОИЗВОДНАЯ», §37 – 43
Контрольная работа
2









§44. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ
Знать и понимать:

  • точка экстремума (максимума, минимума) функции;

  • стационарная точка, критическая точка функции;

  • алгоритм исследования функции на монотонность и экстремумы;

  • алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на промежутке;

  • понятие о непрерывности функции.

Уметь:

  • исследовать функции и строить их графики с помощью производной;

  • решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;

  • решать геометрические, физические, экономические и другие прикладные задачи, в том числе задачи на наибольшие и наименьшие значения с применением аппарата математического анализа.



4






181
Исследование функций на монотонность, п. 1



1






182
Отыскание точек экстремума, п. 2



1






183

184
Применение производной для доказательства тождеств и неравенств, п. 2.



2









185

186
§45. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ



2












§46. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ ВЕЛИЧИН



5






187

188
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке, п. 1



2






189

190

191
Задачи на отыскание наибольших и наименьших значений величин, п.2




3












192

193
Контрольная работа № 7 по теме: «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ», §44 – 46
Контрольная работа
2












БЛОК 10 (ГЕОМЕТРИЯ)




ГЛАВА IV.

ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цель: обобщить изученный в базовой школе материал о векторах на плоскости, дать систематические сведения о действиях с векторами в пространстве.
8









§1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ
Знать и понимать:

  • понятие вектора на плоскости (из курса базовой школы);

  • понятие вектора в пространстве;

  • правила сложения, вычитания и умножения вектора на число;

  • понятие компланарных векторов;

  • правило сложения для трех некомпланарных векторов (правило параллелограмма);

  • теорема о разложении любого вектора по трем некомпланарным векторам

Уметь:

  • использовать векторный метод при решении задач;

  • выполнять действия над векторами в пространстве;

  • раскладывать вектор по трем некомпланарным векторам;

  • доказывать теоремы



2






194

195
Понятие вектора. Длина вектора. Коллинеарные векторы. Равенство векторов, п. 34, 35



2












§2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО



2






196
Сложение и вычитание векторов. Сумма нескольких векторов, п. 36, 37



1






197
Умножение вектора на число, п. 38. Действия над векторами, п. 34-38



1









§3. КОМПЛАНАРНЫЕ ВЕКТОРЫ



3






198
Компланарные векторы, п. 39



1






199
Правило сложения трех некомпланарных векторов (правило параллелепипеда), п. 40



1






200
Разложение вектора по трем некомпланарным векторам, п. 41



1






201
Контрольная работа № 5 по теме: «ВЕКТОРЫ В ПРОСТРАНСТВЕ», п. 34-41
Контрольная работа
1





1   2   3   4   5