Формулы суммы n первых членов арифметической прогрессии
 Скачать 55.24 Kb.
|
| МБОУ « Основная общеобразовательная Владимировская школа» Урок по алгебре 9 класс «Формулы суммы n первых членов арифметической прогрессии" Учитель: Овчарова Л. В. 2013 Тема: "Формулы суммы n первых членов арифметической прогрессии". Тип урока: Урок изучения нового материала.Класс: 9. Продолжительность урока: один академический час. Цели и задачи: образовательные - познакомить учащихся с выводом формулы сумм n первых членов арифметической прогрессии; научить учащихся применять полученные формулы при решении задач. развивающие - сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации. воспитательные - прививать учащимся интерес к предмету посредствам применения информационных технологий (с использованием компьютера), решения исторических задач;. Ход урока
1. Устный фронтальный опрос:
(bn): 7; 5; 3; 1; -1; … (xn): 2; 2,2; 2,6; 3,2; 4; … (cn): 6; 12; 18; 24; 30; … 2. Задания для индивидуальной работы у доски:
Тест да нет  II. Актуализация знаний Задача. Текст лектора. Новый русский решил отгородить бассейн на даче фигурной стеной. Позвав строителей, начал объяснять. - В нижний ряд укладывается 19 блоков, на него кладётся 17 блоков, затем 15 и так далее. Всего 8 рядов. «Арифметическая прогрессия какая-то получается», - произнес бригадир. Прав бригадир? Выпишите числа, соответствующие количеству блоков каждого ряда: 19, 17, 15, 13, 11, 9, 7, 5. Получили последовательность чисел. Опишите её. 2. Придумайте арифметическую прогрессию. Кто хочет доказать, что придуманная им последовательность чисел является ар. пр. Каким еще способом можно доказать? Найдите 20 член этой прогрессии. III. Обьяснение нового материала Задача Рабочий выложил плитку следующим образом: в первом ряду - 3 плитки, во втором - 5 плиток и т.д., увеличивая каждый ряд на 2 плитки. Сколько потребуется рабочему плиток, чтобы выложить 6 рядов Решение: Составьте к задаче последовательность из 6 чисел: 3, 5, 7, 9, 11,13 Нетрудно убедиться, что данная последовательность является арифметической прогрессией. Чтобы узнать количество всех плиток, надо узнать сумму этих чисел, т.е найти сумму первых 6 членов ар.прог. Подумайте как найти количество всех плиток (Ответы учеников) Д а, можно решить эту задачу непосредственным сложением чисел. Но этот способ не рационален. А если бы перед вами стояла задача: найти S100, как вы думаете сколько времени вам потребовалось? Рассказывают, что, когда, великий немецкий математик Карл Гаусс учился в начальной школе, преподаватель предложил ученикам самостоятельно найти сумму ряда от 1 до 100. Он предполагал, что ученики будут складывать эти числа по порядку, на что потребуется не менее 10 минут. Какого же было его удивление, когда маленький Карл через 1-2 минуты заявил, что он задание выполнил и дал правильный ответ. Как же так быстро далось маленькому мальчику найти ответ? Сам Гаусс объяснял это так: "Я заметил, что 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101 и т. д. Пара ровно отстоящих от краёв ряда чисел даёт 101 и последняя пара средних чисел даёт 101 = 50 + 51. Числа, взятые по паре с начала и с конца ряда встречаются в середине после 50 сложений этих пар. Поэтому надо 101 x 50 = 5050. Это число и будет суммой всех 100 чисел". Воспользуйтесь идеей Гаусса для решения задачи про плитки. Что получилось? А теперь попробуйте решить эту же задачу, но для 5 рядов. Можно ли решить эту задачу тем же самым сособом? Почему? Значит существует другой способ решения данной задачи. 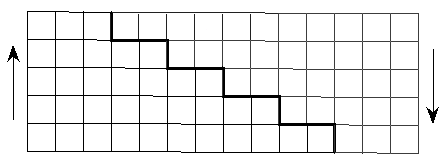 Рис. 1 Сумму 3+5+7+9+11 можно изобразить так, как показано на рис. 1 и из двух таких фигурок составить прямоугольник .Продолжим рассуждения: S = 3 + 5 + 7 + 9 + 11. Напишем в обратном порядке: S = 11 + 9 + 7 + 5 + 3. И сложим эти равенства: S = 3 + 5 + 7 + 9 + 11 + + 11 + 9 + 7 + 5 + 3. В каждом столбце стоят 2 числа, дающие в сумме 14. Поэтому: 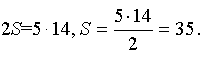 Подтвердим, что применяя этот способ, можно легко найти S100 натуральных чисел.(Самостоятельная работа учащихся) Во всех задачах мы находили Sn. Выведем формулу Sn для общего случая. Вывод: в общем случае будет n столбцов с одинаковой суммой, равной сумме первого и последнего членов. Поэтом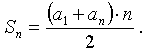у  Вернёмся на дачу к нашим героям. (компьютерная программа: диск 1С: Репетитор. Математика (часть I). Алгебра. Прогрессии. Строим стену). Текст лектора: Вернёмся на дачу к нашим героям. Как по - быстрее вычислить количество блоков в фигурной стене? Ребята, найдите ответ задачи. Что получилось? IV. Первичное закрепление №369, № 370 Готовимся к ГИА Решение задач из сборника Лысенко
Решение задач из сборника Лысенко
Решение задач из сборника Лысенко
Решение задач из сборника Лысенко
|