Программа по алгебре и началам анализа 11 класс (базовый уровень) Пояснительная записка
 Скачать 480.84 Kb. Скачать 480.84 Kb.
|
| 19 | Правила дифференцирования | 1 | Комбинированный | Взаимопроверка в парах. Работа с текстом | Формулы дифференцирования, правила дифференцирования, дифференцирование суммы, произведения, частного; производная сложной функции | Знают: как находить производные суммы, разности, произведения, частного; производные основных элементарных функций. Умеют: использовать для решения познавательных задач справочную литературу. (Р) | Умеют: выводить формулы нахождения производной; вычислять скорость изменения функции в точке; работать с учебником, отбирать и структурировать материал; передавать информацию сжато, полно, выборочно. (П) | Опорные конспекты учащихся | Использование справочной литературы, а также ресурсов Интернет, повтор. Простейшие уравнения В5 (2-3 задачи) п.46 №802-806(четные) | |||||
| 20 | 1 | Учебный практикум | Практикум, фронтальный опрос, работа с раздаточным материалом | Умеют: находить производные суммы, разности, произведения, частного; производные основных элементарных функций; объяснять изученные положения на самостоятельно подобранных конкретных примерах. (П) | Умеют: выводить формулы нахождения сложной функции; объяснять изученные положения на самостоятельно подобранных конкретных примерах. (ТВ) | Слайд лекция «Производная | Работа со справочной литературой повтор. Простейшие уравнения В5 (2-3 задачи) п.46 №807-811(четные) | |||||||
| 21 | 1 | Проблемный | Проблемные задачи, фронтальный опрос, решение упражнений | Умеют: записывать формулой функцию f(g(x)) и находить ее область определения и множество значений; оценивать информацию, факты, процессы, определять их актуальность. (П) | Умеют: записывать формулой функцию f(g(x)), находить ее производную и выяснять, при каких значениях переменной производная принимает положительные и отрицательные значения. (ТВ) | Опорные конспекты учащихся | Составление обобщающих информационных таблиц, повтор. Простейшие уравнения В5 (2-3 задачи) п.46 №812-815(четные) | |||||||
| 22 | Производные элементарных функций | 1 | Комбинированный | Фронтальный опрос. Решение качественных задач. Решение задач | Элементарные функции, производная показательной функции, производная логарифмической функции, производная тригонометрических функций | Знают: производные элементарных функций. Умеют: осуществлять поиск нескольких способов решения, аргументировать рациональный способ, проводить доказательные рассуждения. (Р) | Умеют: выводить формулы производных элементарных функций; проводить информационно-смысловой анализ текста; выбирать главное и основное; работать с чертежными инструментами. (П) | Слайд лекция «Производная | Поиск нужной информации в различных источниках повтор. Значения выражений В7 (10 выражений) п.47 №831-833(четные) | |||||
| 23 | 1 | Учебный практикум | Построение алгоритма действий, решение упражнений | Умеют: находить производные элементарных функций сложного аргумента; самостоятельно искать и отбирать необходимую для учебных задач информацию. (П) | Умеют: находить производную любой комбинации элементарных функций; воспроизводить прослушанную и прочитанную информацию с заданной степенью свернутости. (П) | Раздаточные дифференцированные задания | Работа со справочной литературой, повтор. Значения выражений В7 (10 выражений) п.47№834-838 (четные) | |||||||
| 24 | 1 | Проблемный | Проблемные задачи, фронтальный опрос, решение упражнений | Умеют: вычислять производные обратных тригонометрических функций; давать оценку информации, факты, процессам; определять понятия, приводить доказательства. (П) | Умеют: решать неравенства вида 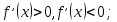 объяснять изученные положения на самостоятельно подобранных конкретных примерах; находить и устранять причины возникших трудностей. (ТВ) объяснять изученные положения на самостоятельно подобранных конкретных примерах; находить и устранять причины возникших трудностей. (ТВ) | Опорные конспекты учащихся | Составление обобщающих таблиц, повтор. Значения выражений В7 (10 выражений) п.47№ 839-842 (четные) , | |||||||
| 25 | Геометрический смысл производной | 1 | Комбинированный | Фронтальный опрос. Решение качественных задач. Решение задач | Угловой коэффициент прямой, касательная к графику функции, геометрический смысл производной, уравнение касательной, алгоритм составления уравнения касательной к графику функции, дифференциал функции | Умеют: составлять уравнения касательной к графику функции по алгоритму; извлекать необходимую информацию из учебно-научных текстов; собирать материал для сообщения по заданной теме. (Р) | Умеют: составлять уравнения касательной к графику функции при дополнительных условиях; приводить примеры, подбирать аргументы, формулировать выводы. (П) | Слайд лекция «Производная | Поиск нужной информации в различных источниках повтор. Значения выражений В7 (10 выражений) п.48 №857,858 (четные) РТ В8 (10 заданий) | |||||
| 26 | 1 | Проблемный | Построение алгоритма действий, решение упражнений | Умеют: определять, под каким углом пересекаются графики функций; работать с учебником, отбирать и структурировать материал; использовать элементы причинно- следственного и структурно-функционального анализа.(П) | Умеют: находить точки, в которых касательная к графику функции параллельна к графику функции y=kx+b; объяснять изученные положения на самостоятельно подобранных примерах. (ТВ) | Опорные конспекты учащихся | Составление обобщающих таблиц, повтор. Значения выражений В7 (10 выражений) п.48№860 (четные) РТ В8 ( 10 заданий) | |||||||
| 27 | 1 | Учебный практикум | Проблемные задачи, фронтальный опрос, решение упражнений | Умеют: показать, что графики двух заданных функций имеют одну общую точку и в этой точке общую касательную, написать уравнение этой касательной; критически оценивать информацию адекватно поставленной цели. (П) | Умеют: находить точки, в которых касательная к кривым параллельны, писать уравнения этих касательных; излагать информацию, обосновывая свой собственный подход. (ТВ) | Раздаточные дифференцированные задания | Работа со справочной литературой, повтор. Значения выражений В7 (10 выражений) п.48№861,862(2) РТ В8 (10 заданий) | |||||||
| 28 | Обобщающий урок по теме «Производная и ее геометрический смысл» | 1 | Урок обобщения и систематизации знаний | Проблемные задания , работа с демонстрационным материалом | | Совершенствуются умения в применении формул производных элементарных функций и правил дифференцирования, а также применение физического и геометрического смысла производной при решении задач. В результате изучения данной темы у учащихся формируются познавательные компетенции: сравнение, сопоставление, классификация объектов по одному или нескольким предложенным основаниям, критериям, а также определение адекватных способов решения учебной задачи на основе заданных алгоритмов | Раздаточные дифференцированные задания | Разработка кластера своего проекта обобщения материала, стр. 254 Проверь себя! | ||||||
| 29 | 1 | Учебный практикум | Решение упражнений, составление опорного конспекта | | | | Раздаточные дифференцированные задания | Разработка кластера своего проекта обобщения материала, сайт Д.Д.Гущина «Решу ЕГЭ» В8 (геометрический смысл производной) | ||||||
| 30 | Контрольная работа № 2 по теме «Производная и ее геометрический смысл» | 1 | Урок контроля, обобщения и коррекции знаний | Индивидуальное решение контрольных заданий | | Умеют: оформлять решения, выполнять задания по заданному алгоритму; работать с чертежными инструментами; предвидеть возможные последствия своих действий. (П) | Умеют: классифицировать и проводить сравнительный анализ, рассуждать и обобщать, аргументированно отвечать на вопросы; контролировать и оценивать свою деятельность; находить и устранять причины возникших трудностей. (ТВ) | Дифференцированные контрольно-измерительные материалы | Создание варианта контрольной работы по теме | |||||
| | Применение производной к исследованию функций | 16 | Основная цель:
| |||||||||||
| 31 | Возрастание и убывание функции | 1 | Комбинированный | Построение алгоритма действий, решение упражнений | Промежутки возрастания и убывания функции, знаки производной, теорема о достаточном условии возрастания функции, промежутки монотонности функции, граничные точки, внутренние точки промежутка, теорема Лагранжа | Умеют: находить интервалы возрастания и убывания функций, заданных в виде многочлена одной переменной; использовать для решения познавательных задач справочную литературу. (Р) | Умеют: находить интервалы возрастания и убывания любой комбинации элементарных функций; формировать вопросы, задачи, создавать проблемную ситуацию, публично выступать. (П) | Проблемные дифференцированные задания | Использование справочной литературы, а также материалов Интернет, Значения выражений В7 (10 выражений) п.49 №899, 900(2,4,6,8),РТ В8 | |||||
| 32 | 1 | Учебный практикум | Практикум, фронтальный опрос | Умеют: строить эскиз графика непрерывной функции, определенной на отрезке; находить и использовать информацию; отделять основную информацию от второстепенной. (П) | Умеют: по графику производной определять промежутки возрастания и убывания функции, решать проблемные задачи и ситуации; извлекать необходимую информацию из источников, созданных в различных знаковых системах. (ТВ) | Раздаточные дифференцированные задания | Составление обобщающих таблиц, повтор. Значения выражений В7 (10 выражений) п.49№902-905 (четные) | |||||||
| 33 | Экстремумы функции | 1 | Комбинированный | Составление опорного конспекта, ответы на вопросы | Окрестность точки, точка максимума функции, точка минимума функции, точки экстремума, критические точки, необходимое и достаточное условие экстремума, стационарные точки функции, теорема Ферма | Умеют: находить стационарные точки заданной функции в виде многочлена одной переменной; воспроизводить прослушанную и прочитанную информацию с заданной степенью свернутости; подбирать аргументы для объяснения решения. (Р) | Умеют: находить точки экстремума любой комбинации элементарных функций; проводить информационно-смысловой анализ; выбирать главное и основное, приводить примеры; работать с чертежными инструментами. (П) | Опорные конспекты учащихся | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.50 №910, 911 | |||||
| 34 | 1 | Учебный практикум | Опрос по теории. Построение алгоритма решения задач | Умеют: строить эскиз графика функции, если задан отрезок, значения функции в концах этого отрезка и знак производной в некоторых точках функции; рассуждать, обобщать, аргументировать решение и ошибки, участвовать в диалоге. (П) | Умеют: доказывать теорему Ферма и теорему о достаточном условии экстремума; работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; осуществлять проверку выводов, положений, закономерностей, теорем (ТВ) | Слайд лекция «Исследование функций» | Использование справочной литературы, а также материалов Интернет, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.50 №912,913 (четные) | |||||||
| 35 | 1 | Учебный практикум | Практикум, решение задач | Раздаточные дифференцированные задания | Составление обобщающих таблиц, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.50№914,915 (четные) | |||||||||
| 36 | Применение производной к построению графиков функций | 1 | комбинированный | Составление опорного конспекта, ответы на вопросы | Горизонтальная асимптота, вертикальная асимптота, построение графика, алгоритм построения графика функции | Знают: применение производной к исследованию функций и построению графиков. Умеют: объяснять изученные положения на самостоятельно подобранных конкретных примерах; публично выступать. (Р) | Умеют: совершать преобразования графиков; объяснять изученные положения на самостоятельно подобранных примерах; выполнять и оформлять тестовые задания, аргументировать решение и найденные ошибки, обобщать. (П) | Слайд лекция «Исследование функций» | Составление обобщающих таблиц, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.51№ 923,924 | |||||
| 37 | 1 | Слайд лекция «Исследование функций» | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.51 №925,929 | |||||||||||
| 38 | 1 | Учебный практикум | Построения алгоритма действия, решение упражнений | Умеют: применять производную к исследованию функций и построению графиков; при построении графика функции придерживаться заданного алгоритма построения; использовать для решения познавательных задач справочную литературу. (П) | Умеют: строить график функции, проводя полное исследование через производную; осуществлять проверку выводов, положений, закономерностей, теорем; находить и устранять причины возникших трудностей. (ТВ) | Раздаточные дифференцированные задания | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.51 №926(2,4), 928(1) | |||||||
| 39 | 1 | Раздаточные дифференцированные задания | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.51 № 927(2,4), 931(2) | |||||||||||
| 40 | Наибольшее и наименьшее значение функции | 1 | Комбинированный | Практикум, фронтальный опрос, решение качественных задач | Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке, алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке, задачи на отыскание наибольшего и наименьшего значений величин, задачи на оптимизацию | Знают: исследование в простейших случаях функции на монотонность. Умеют: находить наибольшие и наименьшие значения функций; находить и использовать информацию. (Р) | Умеют: находить наименьшее и наибольшее значение функций на интервале; составлять текст в научном стиле; использовать данные правила и формулы, аргументировать решение, формировать умение правильно оформлять работу. (П) | Опорные конспекты учащихся | Поиск нужной информации по заданной теме, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.52 №937, РТ В14 | |||||
| 41 | 1 | Опорные конспекты учащихся | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.52 №938, РТ В14 | |||||||||||
| 42 | 1 | Учебный практикум | Построение алгоритма действий, решение упражнений | Умеют: исследовать в простейших случаях функции на монотонность, находить наименьшее и наибольшее значение функции; использовать компьютерные технологии для создания базы данных. (П) | Умеют: решать геометрические задачи на нахождение наибольших и наименьших значений величин; использовать для решения познавательных задач справочную литературу; самостоятельно выбирать критерии для сравнения, сопоставления, оценки и классификации объектов. (ТВ) | Тестовые материалы | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.52 № 939, РТ В14 | |||||||
| 43 | 1 | Учебный практикум | Тестовые материалы | Работа со справочной литературой, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.52 № 942,943 РТ В14 | ||||||||||
| 44 | 1 | Проблемный | Проблемные задачи, фронтальный опрос, решение упражнений | Умеют: находить наибольшие и наименьшие значения функций, заданных на отрезке, интервале; работать с учебником, отбирать и структурировать материал; выбирать и использовать знаковые системы адекватно познавательной и коммуникативной ситуации. (П) | Умеют: решать алгебраические задачи на нахождение наибольших и наименьших значений величин; передавать информацию сжато, полно, выборочно; излагать информацию, обосновывая свой собственный подход; самостоятельно создавать алгоритм познавательной деятельности для решения задач творческого и поискового характера. (И) | Слайд лекция «Исследование функции» | Составление информационных таблиц, повтор. Задачи прикладного содержания В12 (2-3 задачи), п.52 №941 РТ В14 | |||||||
| 45 | Обобщающий урок по теме «Применение производной к исследованию функций» | 1 | Урок обобщения и систематизации знаний | Проблемные задания , работа с демонстрационным материалом | | Совершенствуются умения в нахождении промежутков возрастания или убывания функции, в нахождении точек максимума и минимума и построения графика функции. При изучении данной темы у учащихся формируются ключевые компетенции: способность самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем, умение мотивированно отказываться от образца, искать оригинальные решения. | Раздаточные дифференцированные задания | Разработка кластера своего проекта обобщения материала, стр. 284 Проверь себя! | ||||||
| 46 | ||||||||||||||