«Проектная деятельность учащихся в процессе обучения математике»
 Скачать 130.61 Kb. Скачать 130.61 Kb.
|
| Тема: «Проектная деятельность учащихся в процессе обучения математике» В современном обществе оказались востребованными такие качества индивидуума, необходимые для успешного функционирования в любой сфере жизни человека, как способность самостоятельно принимать решения о действии, анализировать и моделировать проблемную ситуацию, предлагать идею решения проблемы и брать на себя ответственность за последствия сделанного выбора, планировать действия и структурировать их во времени, строить взаимоотношения в коллективе и уметь продуктивно участвовать в коллективной деятельности и т. д. Но подобные целевые установки в принципе отсутствуют в традиционной системе образования. Возникшие противоречие между запросами социума к образованию и сложившейся школьной практикой призвано разрешить введение в систему обучения такой формы работы, как проектная деятельность. Проектная деятельность (или проектирование) – это обязательно практическая деятельность. Ее ведущая характеристика, как у любой деятельности, - целеполагание. Ставя задачу, формулируя цель проекта, учащиеся ищут под эту конкретную цель средства ее достижения. Это и есть основное назначение проектной деятельности: формирование у школьников способности действовать, оказавшись в новой ситуации, увидеть эту ситуацию как поле собственных действий по ее преобразованию. При этом речь идет о способности просчитать реальную практическую ситуацию через призму приобретенных в школе знаний, идя от задачи к поиску средств для ее решения. Последнее замечание имеет принципиальное замечание: само по себе включение элементов проектирования в обучение не даст ожидаемых результатов, если проектная деятельность будет осуществляться отдельно от основного образовательного процесса. Предметные знания, полученные в учебной работе, должны служить ресурсом учебного проекта, а выполнение проекта, в свою очередь, должно приводить к развитию познавательного интереса к содержанию обучения. Иными словами, при организации проектной деятельности важна сопряженность пространств учебной и проектной работ. Ключевыми моментами (смысловыми центрами) проектной деятельности являются:
Именно эти взаимосвязанные моменты задают структуру проектной деятельности, определяю ее основу. Изменения, произошедшие в последние годы в школьном математическом образовании, значительно расширили возможность организации проектной деятельности при изучении курса математики. Это связано, прежде всего с введением в содержание образования новой вероятностно-статистической линии. Она позволяет сделать идеей проекта рассмотрение реального социального аспекта нашей действительности. Программа курса математики предусматривает знакомство учащихся с элементами описательной статистики, с наглядными способами предъявления информации. Знания, полученные при изучении этого материала, могут и должны использоваться как средства в ходе проектной деятельности. Не следует забывать и о существенной роли проектов во внеурочной деятельности. Проектом может стать организация и подготовка недели математики, олимпиады, математической регаты и т. п. Выполняя проект, учащиеся будут работать с научно-популярной и математической литературой, решать и отбирать задачи, знакомиться с историей математики. Надо заметить, что возможности самостоятельных проектов по математике ограниченны, однако математическое содержание может являться существенной, но не основной частью межпредметного проекта, выполняя роль инструментария. Приведем пример таких исследований по литературе: как различаются по длине слова в стихотворениях различных стихотворных размеров, в произведениях различных поэтов, писателей. Математика здесь представлена описательной статистикой. Рассмотренные примеры – это примеры проектов, которые условно можно было назвать прикладными. Другой тип математического проекта, который назовем исследовательским. Сущность такого рода проектов – это рассмотрение некоторой математической проблемы. Последующие суждения и приведенные примеры изложили Мерлина Н. И., доктор педагогических наук, кандидат физико-математических наук, профессор, профессор кафедры прикладной математики Чувашского государственного университета им. И. Н. Ульянова, г. Чебоксары. Уткина Т. И., доктор педагогических наук, профессор, заведующий кафедрой алгебры, геометрии, теории и методики обучения математике Орского гуманитарно-технологического института ГБОУ ВПО «Оренбургский государственный университет», г. Орск. По их мнению, проведение эксперимента по математике, способ развития индивидуальной проектно-исследовательской деятельности. Современные изменения, происходящие в обществе, существенным образом повлияли на роль и приоритеты общего образования. Целесообразность подготовки выпускника общеобразовательной школы к инновационным преобразованиям общества стало жизненно необходимым условием его самоопределения и самореализации. В качестве одного из механизмов создания указанных условий, по нашему мнению, следует рассматривать приобретение опыта к анализу и исследованию ситуаций, с которыми выпускнику приходится сталкиваться после окончания школы при выборе своего профессионального пути. Неслучайно в Федеральном стандарте среднего (полного) общего образования индивидуальная проектно-исследовательская деятельность учащихся рассматривается в качестве класса универсальных учебных действий, которые представлены в качестве конечных результатов образования [8]. Поставленная задача является в настоящее время одним из приоритетных направлений содержания общего образования, которое должно прослеживаться на всех школьных предметах, в том числе и на математике. Процесс обучения математике в 10–11 классах позволяет на его основе развивать индивидуальную проектно-исследовательскую деятельность учащихся. Это связано с тем, что, во-первых, курс математики 10–11 классов является завершающим, систематизирующим и обобщающим разделом школьной математики. Во-вторых, содержательный компонент математики 10–11 классов раскрывает основные идеи и пути дальнейшего развития математического знания, использование которого позволяет усвоить фундаментальные основы построения математического анализа, установить связи с предметами естественнонаучного цикла. В-третьих, в процессе обучения математике в 10–11 классах учащиеся овладевают математическим инструментарием – математическими моделями. Их применение позволяет показать учащимся универсальность математического аппарата как средства описания различных явлений и процессов. Организация математической деятельности предполагает мысленное экспериментирование с тем или иным материалом с целью прослеживания его взаимосвязи. Как видим, резерв содержательного и процессуального компонентов процесса обучения математике в 10–11 классах обладает большим потенциалом для развития индивидуальной проектно-исследовательской деятельности учащихся. Под индивидуальной проектно-исследовательской деятельностью в исследовании понимается процесс достижения цели, который выстраивается по индивидуальной образовательной траектории на основе самостоятельного поиска теоретических знаний, предвидения и прогнозирования способов и процессов деятельности, и завершается реальным практическим или теоретическим результатом. Создание индивидуальной образовательной траектории предполагает выявление этапов индивидуальной проектно-исследовательской деятельности. Основываясь на результатах работы Н. В. Матяш [4], в исследовании были выделены этапы индивидуальной проектно-исследовательской деятельности: - ситуационно-исследовательский этап, целью которого является появление интереса у обучающихся на основе действия учебно-познавательных мотивов, осознание проблемы и формулирование цели деятельности, её планирование, поиск и отбор информации по теме, выбор средств и инструментария; - инструментально-операциональный этап, целью которого является обработка и осмысление информации обучающимся, самоконтроль деятельности, установление соответствия её поставленной цели, выполнение соответствующих технологических операций, предусмотренных разработанным планом, оформление результата; - рефлексивно-оценочный этап, его цель – формулировка выводов по соответствию результатов деятельности с заданной целью, проверка рациональности выполненных действий, поиск альтернативных путей решения и обозначение дальнейших перспектив развития проблемы, представление результата своей деятельности в виде сообщения, презентации, публикации и др. Этапы индивидуальной проектно-исследовательской деятельности тесно связаны с этапами процесса обучения математике, на каждом из которых используются задачи-ситуации. Под задачей-ситуацией понимается данная в определенных условиях и обстоятельствах цель деятельности, которая достигается определенной последовательностью действий, соответствующих сложившейся ситуации. Последовательность действий предполагает: осознание ситуации, построение модели, её теоретическое обоснование и практическое применение. В соответствии с этапами развития индивидуальной проектно-исследовательской деятельности выделены виды задач-ситуаций: на прогнозирование, на планирование, на создание проекта. Различные математические ситуации, возникающие в процессе решения задач-ситуаций, разрешимы с использованием эксперимента. Гибкость и вариативность решения математической ситуации, установление причинно-следственных, внутрипредметных и межпредметных связей в процессе проведения эксперимента также подтверждает целесообразность его использования при осуществлении проектно-исследовательской деятельности в процессе обучения математике в 10–11 классах. По мнению В. И. Загвязинского, эксперимент – самый точный метод изучения явлений, фиксирования фактов, слежения за изменением и развитием объекта исследования [2]. В. В. Давыдов в своих работах употребляет понятие «мыслительный эксперимент», который, по мнению автора, нацеливает учащихся на получение знаний как результата преобразования заданного материала, позволяющего вскрыть в нём существенные отношения и проследить происхождение внешних проявлений изучаемого материала [1]. В широком смысле эксперимент представляет собой целенаправленное и жестко контролируемое действие исследователя на объект для изучения его различных сторон, связей и отношений. По мнению Л. А. Михайлова [5], С. Х. Карпенкова [3], В. В. Налимова [7] и др., в любом эксперименте можно выделить следующие этапы: - подготовительный этап ориентирован на теоретическое обоснование эксперимента, формулировку гипотезы, его планирование, создание модели, выбор условий и средств исследования; - этап сбора экспериментальных данных направлен на работу с моделью, выполнение соответствующих технологических операций, многократную повторность измерений и строгий учёт факторов, влияющих на исследуемый объект; - этап обработки результатов содержит анализ и интерпретацию результатов эксперимента, сопоставление их с гипотезой, установление причинно-следственных связей между заданными условиями и характеристиками исследуемого объекта. На всех этапах эксперимента важна мыслительная деятельность экспериментатора, включающая отделение фактов, непосредственно влияющих на объект исследования, искусственное выделение некоторых его свойств, признаков или отношений, которые и являются предметом изучения, что способствует глубокому пониманию сути явлений и процессов. На основе проведённого в исследовании контент-анализа видно, что этапы индивидуальной проектно-исследовательской деятельности и этапы эксперимента находятся в тесной связи, повторяют друг друга или являются взаимозаменяемыми (рис.1) 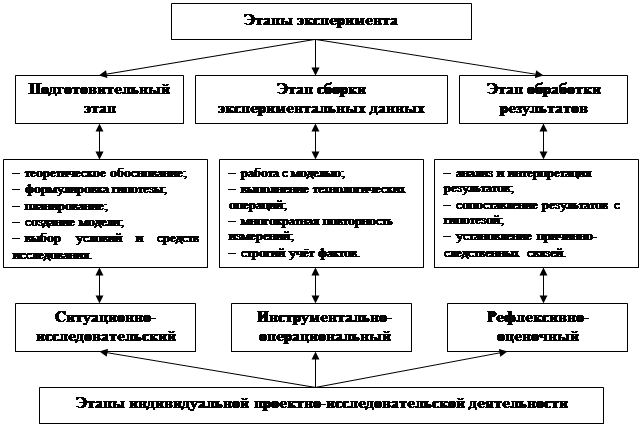 Рис. 1. Сопоставление этапов индивидуальной проектно-исследовательской деятельности с этапами эксперимента Приведём пример задачи-ситуации на прогнозирование, направленной на развитие индивидуальной проектно-исследовательской деятельности, для решения которой необходимо использование эксперимента. Тема: «Общие методы решения уравнений» [6]. Цель: сформировать представление учащихся об общих идеях и методах решения уравнений. 1. Прочитайте теоретический материал об общих методах решения уравнений и выделите особенности каждого из них (подчеркните их в тексте): Метод замены уравнения Такой метод решения уравнений применяется: - при решении показательных уравнений, когда переходим от уравнения - при решении логарифмических уравнений, когда переходим от уравнения - при решении иррациональных уравнений, когда переходим от уравнения Этот метод можно применять только в том случае, когда функция Метод разложения на множители Уравнение 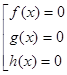 . Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние. . Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние.Метод введения новой переменной Если уравнение  , где , где Функционально-графический метод Идея этого метода решения уравнения 2. Установите соответствие между решёнными уравнениями и методом их решения (рис. 2):
Рис. 2. Соответствие между уравнениями и методом их решения 3. Решите уравнения и разбейте предложенные уравнения на группы по методам решения (табл. 1). Таблица 1 Примеры уравнений по методам решения
Использование задач-ситуаций, для решения которых необходимо применять эксперимент, выступает механизмом развития индивидуальной проектно-исследовательской деятельности обучающихся в учебном процессе по математике в 10–11 классах. В заключении небольшой перечень тем для проектов по математике. Проекты прикладного характера
Проекты исследовательского характера
Используемая литература 1. Давыдов В. В. О понятии развивающего обучения // Педагогика. – 1995. – №1. – С. 29-39. 2. Загвязинский В. И. Методология и методы психолого-педагогического исследования: учеб. пособие для студентов пед. вузов. – М.: Академия, 2001. – 202 с. 3. Концепции современного естествознания: учебник для вузов / [под ред. С. Х. Карпенкова]. – М.: Высшая школа, 2003. – 488 с. 4. Матяш Н. В. Инновационные педагогические технологии проектное обучение: учебное пособие для студентов учреждений ВПО. – М.: Издат. центр «Академия», 2011. – 144 с. 5. Михайлов Л. А. Концепции современного естествознания [Электронный ресурс]. – Режим доступа: http: www.e-reading-lib.org/bookreader.php/133233/Mihaiilov_-Koncep.html 6. Мордкович А. Г., Смирнова И.М. [и др.]. Математика. 11 класс: учебник для учащихся образовательных учреждений (базовый уровень). – 7-е изд., испр. – М.: Мнемозина, 2012. – 416 с. 7. Налимов В. В. Теория эксперимента. – М.: Наука, 1971. – 215 с. 8. Федеральный государственный образовательный стандарт среднего (полного) общего образования [Электронный ресурс]. – Режим доступа: http: Standart.edu.ru 9. Шамало Т. Н. Теоретические основы физического эксперимента в развивающем обучении: учебное пособие к спецкурсу. – СГПИ, 1990. – 96 с; |
 ример 1:
ример 1: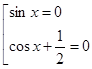 ,
, 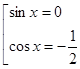 ,
,  ,
,  .
.