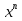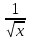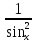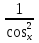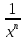Площадь криволинейной трапеции
 Скачать 114.02 Kb. Скачать 114.02 Kb.
|
                               Денисова Ольга Евгеньевна. Денисова Ольга Евгеньевна. Проект урока по алгебре и началам анализа в 11 а классе МБОУ «СОШ №4». Тема: Площадь криволинейной трапеции. Тип урока: обобщение материала, работа в парах и группах, использование компьютерных технологий для организации учебного процесса. Характеристика урока: данный урок входит в главу «Первообразная и интеграл», учащиеся овладели определением первообразной, правилами нахождения первообразной, определением криволинейной трапеции, формулой нахождения её площади. Учебные возможности класса: учащиеся имеют навыки работы в группе, у них достаточно развиты познавательные способности, привит интерес к предмету, учащиеся хорошо работают по алгоритму, при постановке проблемы не все учащиеся находят самостоятельное её решение, имеют разную скорость протекания мыслительных процессов. Цель: - Систематизировать, расширить знания по данной теме. Оборудование: экран, презентация, тест с электронного учебника, папки с приложениями, оценочные листы. Урок проходит по этапам. Результаты каждого этапа учащиеся заносят в оценочные листы. Задачи урока:
Методы обучения: словесные (диалог, полилог, беседа); Наглядные( работа с презентацией); Частично-поисковые (решение проблемной ситуации); Индуктивные (развитие умения общаться, высказывать своё мнение, доказывать его); Дедуктивные (анализ изученного, применение знаний к решению задач, обобщение) Формы обучения: парная и групповая Форма контроля: самоконтроль. Технологии: технология групповой работы -технология деятельностного подхода -проблемно-диалогического обучения. Предполагаемый результат: освоение темы, мотивирование на новые способы нахождения площади криволинейной трапеции, умение работать в группе.
Денисова Ольга Евгеньевна. Задание 2. План урока в логике системно-деятельностного подхода. Тема урока: Площадь криволинейной трапеции. Тип урока: урок обобщения материала, работа в парах, группах, использование компьютерных технологий для организации образовательного процесса. Цель:
Задачи:
Оборудование: экран, презентация, тест с электронного учебника, папки с приложениями, индивидуальные оценочные листы. Урок происходит по этапам. Результаты каждого этапа учащиеся заносят в оценочные листы:
1этап урока .Мобилизирующий этап.(8-10мин) (раздаточный материал и оценочные карты выданы каждому ученику) (Работа в парах -отвечают друг другу на вопросы) 1Дайте определение первообразной для функции f(x) на заданном промежутке. 2.Сформулируйте основное свойство первообразной. 3.В чём заключается геометрический смысл основного свойства первообразной? 4.Заполните таблицу первообразных
5.Запишите 3 правила нахождения первообразных. 6. Какие из заштрихованных фигур являются криволинейными трапециями? у у у 0 в Х а в х 0 а в Х 7. Какая фигура называется криволинейной трапецией? (Выставляют баллы в оценочные лист). 2 этап- Проверка домашней работы-10мин. Руководителям групп было дано задание по решению задач на нахождение площади фигуры не являющейся криволинейной трапецией.( Чертёж и решение заготовлены перед уроком. Руководитель одной из групп объясняет ребятам свой способ решения незнакомой для них проблемы. Учитель корректирует решение и его оформление.) - Определите тему урока. Исходя из темы сформулируйте цель урока. 3 этап. Закрепление (диф. работа в 3группах- руководители групп выбраны самими учащимися)-10 мин. 1 группа: Найдите площадь фигуры, ограниченной линиями y(x)=x2+2, g(x)=4-x 2 группа: Найдите площадь фигуры, ограниченной линиями y(x)=-x2-4x, g(x)=x+4 3 группа: Найдите площадь фигуры, ограниченной линиями y(x)=4/x2, g(x)=-3x+7 Руководитель группы выставляет баллы в оценочные листы, показывает решение на доске. Домашнее задание: по выбору. Базовый уровень-№ 355 (в,г), 356 (в,г) Повышенный уровень-задания на карточках, которые разложены на столах у каждой группы учащихся. 4 этап урока.Тест к п.29 (тест на электронном приложении к учебнику А.Н. Колмогорова).-12 мин.
А)4,5 Б)1,5 В)3 Г)6 2. Вычислить площадь фигуры, ограниченной линиями у=0; y=cosx, Х= 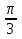 ; х= ; х=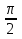 А)1 Б) 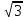 В) В)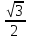 Г)2 Г)23. Вычислить площадь фигуры, ограниченной линиями у= 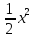 ; у=0; х=6. ; у=0; х=6.А)3 Б) 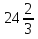 В)6 Г)36 В)6 Г)364. Вычислить площадь фигуры, ограниченной линиями у= 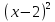 ; х=0; у=0. ; х=0; у=0.А)2 Б) 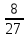 ; В) 2 ; В) 2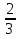 ; Г)3 ; Г)35. Вычислить площадь фигуры, ограниченной линиями у=3-3 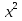 ;у=0. ;у=0.А)2 Б)4; В)3; г)6 6. Вычислить площадь фигуры, ограниченной линиями у= 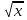 ; у=0; х=9. ; у=0; х=9.Ответ: 7. Вычислить площадь фигуры, ограниченной параболой у=-3 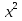 + 18х -15 и осью абсцисс. + 18х -15 и осью абсцисс.Ответ: 8. Вычислить площадь фигуры, ограниченной линиями у= 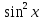 + +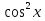 + +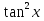 ; ; у=0; х=0; х= 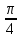 . .Ответ: Проверка теста.(1 ученик, справившийся с тестом быстрре других, отмечает ответы в электронном варианте, ученики сверяют ответы, выведенные на экран с помощью проектора и выставляют себе баллы в оценочный лист). Ученики подсчитывают общее количество баллов, переводят их в оценку. -Рефлексия.-3мин В каких навыках продвинулись дальше? Что нового узнали? Какой отметкой оцениваете свои знания по теме «Площадь криволинейной трапеции»? - Спасибо за урок! Денисова Ольга Евгеньевна. Задание 3. «Рефлексивный анализ собственной педагогической деятельности в контексте ФГОС ООО». В 2010 году я начала работать над темой «Проблемно-диалогическое обучение». Одной из причин, побудившей меня взять эту тему, было осознание того, что работая в классах с разным уровнем обученности детей, очень сложно выстроить урок так, чтобы все ребята были одновременно задействованы на уроке. Чтобы «сильные» ученики не скучали, в то время, когда идёт отработка материала со «слабыми» учениками, чтобы и те и другие могли развиваться на основе освоения универсальных способов деятельности. Начала работу с изучения литературы. Через интернет нашла учителей, работающих над этой темой, изучила их опыт, посмотрела представленные планы и конспекты уроков. Стала применять технологию на уроках в 5 классе. Класс был небольшой, ребята имели хорошую базу начальной школы. Разделила их на 3 группы, руководителей назначила сама, объяснила им меру их ответственности за усвоение учебного материала каждым членом группы. Сначала было не всё гладко: руководители пытались больший объём работы делать сами и с теми, кто хорошо усвоил материал, остальные откровенно списывали у них. Тогда на помощь пришли разноуровневые задания. Ребята стали успевать решать свои задания, проверять и помогать членам группы. Когда было предложено членам групп найти сложные задания для руководителей, они заинтересовались не только поиском, но и способами их решения. Таким образом, класс стал более дружным, меньше стали ябедничать, смеяться над ошибками товарищей, помогать усвоить материал, стали самостоятельно ставить цель урока, самооценка стала более адекватной. Качество знаний стало лучше, кроме этого ребята с удовольствием принимали участие в неделе математики. Первыми принесли ответы на викторины, самостоятельно готовили конкурсные домашние задания. В 2011-2012 учебном году переехала в Нарьян-Мар. Стала работать в старших классах. Навыков обучения в группах и парной работе у детей не было. Попытки применить технологию проблемно-диалогического обучения в полном объёме не удалась. Попробовала применить её элементы: постановка проблемы, целеполагание, самостоятельное осознание того как и где можно применять полученные на уроке знания. Во втором полугодии прошлого учебного года девятиклассники стали через интернет ресурсы в режиме онлайн прорешивать КИМы по математике, предлагать свои способы решения. На элективных курсах делиться своим нарешенным материалом, консультироваться не только с учителем, но и одноклассниками. В 10 классе ребята имели хорошие базовые знания за курс основной школы, кроме этого дети очень дружные, ответственные, поэтому в работе с ними более быстро удалось организовать работу в логике системно- деятельностного подхода. Они очень ответственно подходили к изучению предложенных проблем, готовили доклады, презентации, исторические справки. В СОШ № 4 есть хорошая традиция: ученики 10 профильных классов пишут курсовые работы, защита которых проходит в марте для учеников социально-гуманитарного профиля и в апреле для естественно-научного профиля. Вот где в полной мере старшеклассники учатся добывать информацию, обрабатывать и применять её. Сейчас эти ребята обучаются в 11 классе. Они решили остаться работать в тех же 3-х группах, что и в прошлом учебном году. Руководители групп не только помогают своим товарищам понять сложные моменты в изучении нового материала, но и оказывают консультационную помощь тем ребятам, которые пропустили уроки. В этом классе разноуровневые задания я предлагаю не только для работы в классе, но и в домашней работе, причём способным ребятам даю задание на опережение изученного материала и даю им возможность на уроке побывать в роли учителя, объяснить одноклассникам тему или предложить свой алгоритм решения задачи. Моя роль заключается в том, чтобы одобрить выбранный способ решения, подкорректировать его, выслушать мнения и предложения других учеников, представить свой способ, ну и, конечно, похвалить ученика за проделанную работу. Я считаю, что системно-деятельностный подход в обучении заставляет учителя искать те методы обучения, которые позволяют развивать ребёнка, проявлять его творческие способности, искать различные методы решения, не бояться ошибаться, понимать, что информацию интереснее добыть и понять самому, чем получить её в готовом виде. Но начинать надо с начальной школы, постепенно приучать детей к тому, что самостоятельное решение проблемы даст более хороший результат, чем просто воспроизведение услышанного или прочитанного. Значит вопросы: чему учить? Как учить? Ради чего учить? будут стоять перед нами - учителями при подготовке каждого урока. |