|
Урок рассчитан на 45 минут. Тип урока : комбинированный. Цели урока      Школа Школа: МАОУ Лицей №1, г. Балаково. Учитель: Ремезова Елена Николаевна, учитель высшей категории. Предмет: алгебра и начала анализа. Учебный план:5 часов в неделю. Класс: 10 (химико-биологический профиль). Тема. Отбор корней при решении тригонометрических уравнений.Место урока в теме. Второй урок из четырех запланированных по данной теме. Дата проведения урока. 29 января 2013 год. Урок рассчитан на 45 минут. Тип урока: комбинированный. Цели урока:
дидактические: сформировать умения применять геометрический метод отбора корней при решении тригонометрических уравнений; совершенствовать навыки решения тригонометрических уравнений различными методами;
развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь;
воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.
Оборудование: компьютер, мультимедийный проектор, экран, презентация «Отбор корней при решении тригонометрических уравнений», листы на каждого ученика для математического диктанта с заготовками числовых окружностей, листы самооценки.
Этапы
урока
|
Содержание урока
|
Время
(мин)
|
Деятельность
|
учителя
|
ученика
|
I
|
Организационный этап.
|
1
|
Приветствие учащихся, проверка готовности к уроку (тетради, ручки, карандаши, линейки).
|
Сообщают об отсутствующих. Записывают в тетради число, классная работа.
|
II
|
Повторение изученного материала.
Математический диктант. (Приложение 1).
Взаимопроверка математического диктанта (Приложение 2).
|
5
3
|
Предлагает написать математический диктант. Читает текст диктанта и демонстрирует его на экран через проектор.
Демонстрирует ответы на экран.
|
Выполняют диктант на листочках, на которых заранее приготовлены числовые окружности.
Выполняют проверку.
|
|
Устно решить простейшие тригонометрические уравнения (Приложение 3).
|
3
|
Уравнения демонстрирует на экран через медиапроектор.
|
Один ученик у доски решения показывает на числовой окружности. Все остальные решают уравнения и внимательно следят за ответами учащихся (фронтальный опрос).
|
|
Перечислите методы решения тригонометрических уравнений, которые мы изучили.
а) замена переменной;
б) разложение на множители;
в) деление обеих частей уравнения на cos(mx) для однородных уравнений первой степени, деление обеих частей уравнения на cos2(mx) для однородных уравнений второй степени.
|
1
|
Задает вопрос и ответы учащихся проецирует на экран.
|
Отвечают на поставленный вопрос.
|
III
|
Изучение нового материала.
|
|
|
|
|
Решить уравнение: 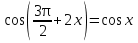 если x∊ если x∊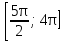 . .
Вопросы:
а) Что нужно сделать, чтобы выполнить предложенное задание?
б) Какими методами мы на прошлом уроке отбирали корни?
в) Как вы думаете, можно ли как-то ещё найти нужные корни?
Давайте данное уравнение решим и отберем корни тремя способами:
1 вариант – перебором корней;
2 вариант – составив двойное неравенство;
3 вариант – отметив корни на числовой окружности.
(Приложение 4).
|
6
|
Задает вопросы.
Следит за решением.
|
Отвечают на поставленные вопросы.
Сначала найти все корни уравнения, а затем отобрать те, которые удовлетворяют заданному условию.
Арифметическим, т.е. перебором значений целочисленного параметра и алгебраическим, составляя и решая двойное неравенство.
Можно, если отметить корни на числовой окружности и рассмотреть заданный промежуток.
Один ученик у доски находит все корни уравнения, а все остальные решают уравнение в тетради.
Затем три ученика у доски отбирают нужные корни разными способами.
|
|
Решить уравнения. При отборе корней используйте геометрический метод. (Приложение 5).
a)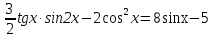 , ,
если x∊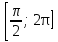 ; ;
б)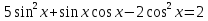 , если x∊ , если x∊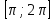
|
10
|
Следит за выполнением задания.
|
Выполняют задания. У доски решает ученик, все остальные в тетрадях
|
IV
|
Самостоятельная работа на закрепление изученного материала.
|
|
|
|
|
Самостоятельная работа в двух вариантах. Обязательно решить одно уравнение, второе дополнительно.
(Приложение 6).
|
10
|
Оказывает индивидуальное консультирование при затруднениях.
|
Выполняют работу. Могут обратиться к учителю за консультацией.
|
|
Взаимопроверка самостоятельной работы. Ответы проецируются на экран.
(Приложение 7).
|
3
|
Проецирует решения на экран.
|
Проверяют работы друг у друга. Результат отмечают в листе самооценки.
|
V
|
Домашнее задание.
(Приложение 8).
|
1
|
Раздает карточки с заданием на дом. Поясняет, что из предложенных пяти уравнений за 3 любые решенные верно уравнения геометрическимметодом выставляется оценка «3», за 4 – «4», за 5 – «5»
|
Читают задания и если возникают вопросы, задают учителю.
|
VI
|
Подведение итогов урока.
Отбор корней при решении тригонометрических уравнений с помощью числовой окружности заметно сокращает время выполнения задания, а также знание нескольких методов отбора корней дает возможность проверки правильности решения.
В листе самооценки подсчитайте количество набранных баллов и поставьте себе оценку за урок.
|
2
|
Выставляет оценку за работу на уроке.
|
Подсчитывают баллы, выставляют оценки.
| Приложение 1.Математический диктант.
Отметьте на числовой окружности точки, соответствующие числам: 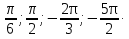
Запишите числа, соответствующие точкам A, B, C числовой окружности
Из числового множества X1=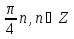 исключите те числа, которые принадлежат множеству X2={ исключите те числа, которые принадлежат множеству X2={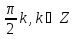 } и запишите получившееся числовое множество X. } и запишите получившееся числовое множество X.
Найдите объединение числовых множеств X1 и X2,
если X 1={ 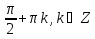 }, X 2={ 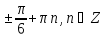 }.
Укажите декартовы координаты заданных точек:
A( 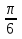 ), В( 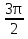 ), С( 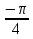 ).
Выделите на числовой окружности следующий промежуток:
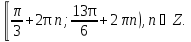 Приложение 2.Ответы к математическому диктанту. Приложение 2.Ответы к математическому диктанту.Вариант 1.
А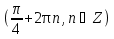 , В( , В(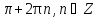 ), С( ), С(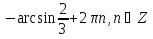 ). ).
X={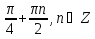 }. }.
X={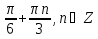 }. }.
A(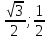 ), В(0; ), В(0;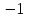 ), С( ), С(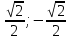 ). ).
Приложение 3.Простейшие тригонометрические уравнения.а) sin x=1; б) sin x= 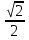 ; в) sin x= 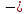 2; г) sin x= 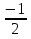 ; д) sin x= 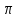 ; е) сos x= 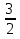 ; ж) сos x=0; з) сos x= 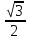 ; и) сos x= 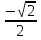 ; к) сos x= 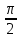 ; л) tg x= 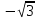 ; м) tg x=3. Ответы к решениям простейших тригонометрических уравнений.а) x= 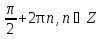 ; б) x 1= 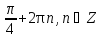 ; x 2= 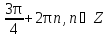 в) корней нет; г) x 1= 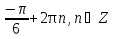 ; x 2= 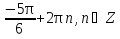 ; д) корней нет; е) корней нет ж) x= 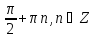 ; з) x 1= 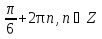 ; x 2= 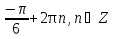 ; и) x 1= 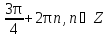 ; x 2= 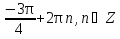 ; к) корней нет л) x= 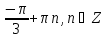 ; м) x=arctg3 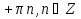 . Методы решения тригонометрических уравнений.а) замена переменной; б) разложение на множители; в) деление обеих частей уравнения на cos(mx) для однородных уравнений первой степени. деление обеих частей уравнения на cos 2(mx) для однородных уравнений второй степени. Приложение 4.Отбор корней разными методами при решении тригонометрического уравнения.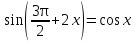 , если 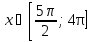 Решение. Решение.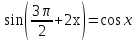 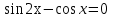 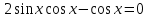 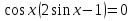 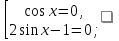 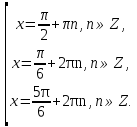 Ответ: Ответ: 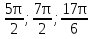 Приложение 5.Отбор корней с помощью числовой окружности. Приложение 5.Отбор корней с помощью числовой окружности.а) 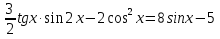 , если x∊ 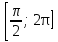 . ОДЗ: 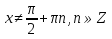 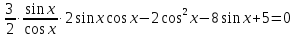 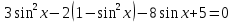 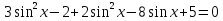 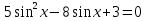 Заменим 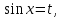 где 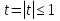 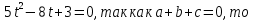 t1=1, t2= t1=1, t2=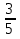 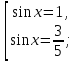 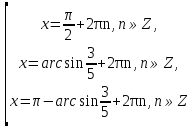 Учитывая ОДЗ 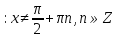 Ответ: Ответ: 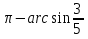 . .б) 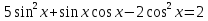 , если x∊ 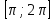 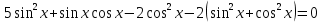 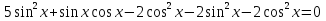 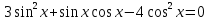 Разделим правую и левую часть уравнения на 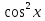 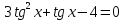 Заменим 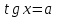 , где 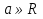 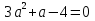 , , так как a+b+c=0, то a 1=1, a 2= 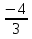 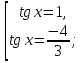 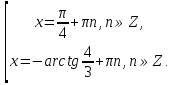 Ответ: Ответ: 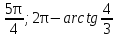 Приложение 6.Самостоятельная работа.Вариант 1. Приложение 6.Самостоятельная работа.Вариант 1.
sin2x=2sin х 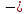 cos х cos х 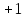 , если х∊ , если х∊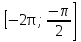 . .
sin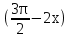 =sin x, если x∊ =sin x, если x∊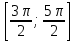 ; ;
Вариант 2.
соs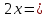 1 1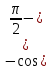 , если x∊ , если x∊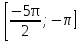 ; ;
sin2x + 4cos x = 2,75, если x∊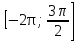 . .
Приложение 7.Решение самостоятельной работы.Вариант 1
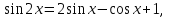 если х∊ 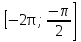 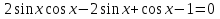 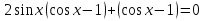 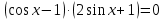 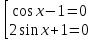 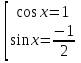 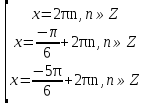 Ответ: Ответ: 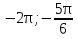
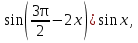 если х∊ если х∊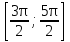
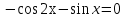 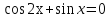 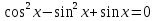 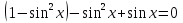 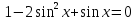 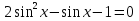 Заменим Заменим 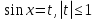 2a2 2a2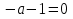 a1=1, a2= a1=1, a2=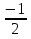 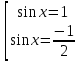 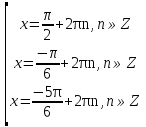 Ответ: Ответ: 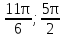 . .Вариант 2.
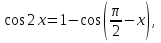 если х если х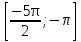
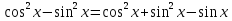 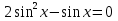 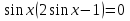 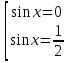 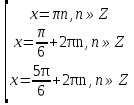 Ответ: Ответ: 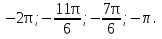
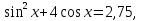 если x если x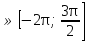
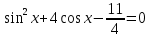 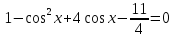 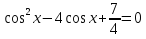 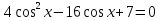 Заменим 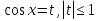 4t 2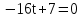 D 1=64 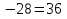 t 1=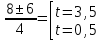 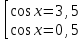 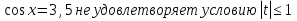 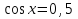 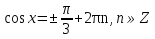 Ответ: Ответ: 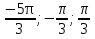 Приложение 8.Домашнее задание. Приложение 8.Домашнее задание.
6 sin2x + cos x 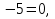 если x∊ если x∊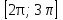 . .
4 cos2x + 4cos (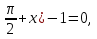 если x∊ если x∊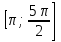 . .
cos 2x + 3 sin2x = 1,25, если x∊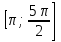 . .
sin 2x = cos x|cosx|, удовлетворяющие условию x  [0; 2 [0; 2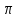 ]. ].
cos x + cos 2x – cos 3x = 1, если x∊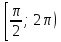 . .
|
|
|
 Скачать 120.43 Kb.
Скачать 120.43 Kb.



 Школа: МАОУ Лицей №1, г. Балаково.
Школа: МАОУ Лицей №1, г. Балаково.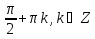 }, X2={
}, X2={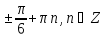 }.
}. 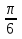 ), В(
), В(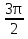 ), С(
), С(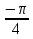 ).
).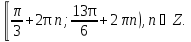
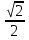 ;
;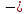 2;
2;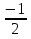 ;
;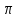 ;
;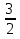 ;
;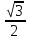 ;
;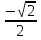 ;
;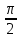 ;
;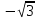 ;
;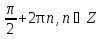 ;
;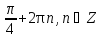 ; x2=
; x2=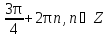
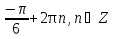 ; x2=
; x2=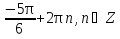 ;
;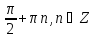 ;
;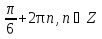 ; x2=
; x2=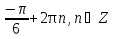 ;
;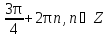 ; x2=
; x2=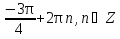 ;
;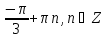 ;
;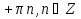 .
.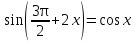 , если
, если 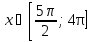
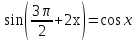
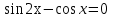
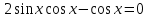
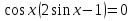
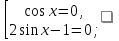
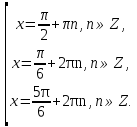
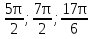
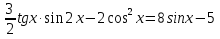 , если x∊
, если x∊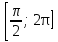 .
.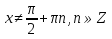
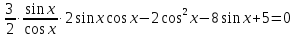
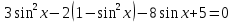
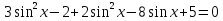
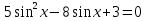
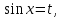 где
где 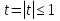
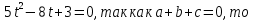 t1=1, t2=
t1=1, t2=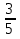
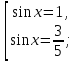
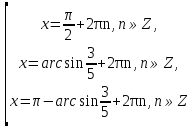
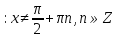
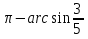 .
.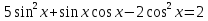 , если x∊
, если x∊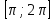
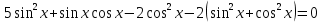
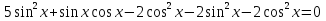
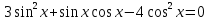
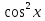
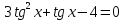
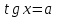 , где
, где 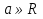
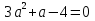 , так как a+b+c=0, то a1=1, a2=
, так как a+b+c=0, то a1=1, a2=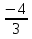
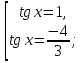
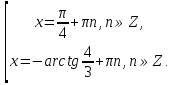
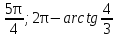
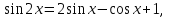 если х∊
если х∊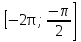
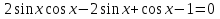
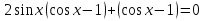
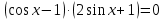
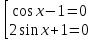
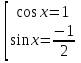
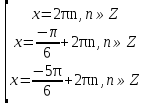
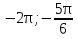
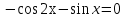
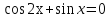
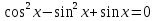
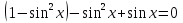
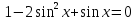
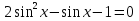
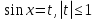
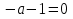
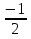
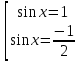
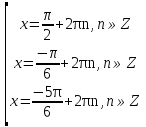
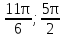 .
.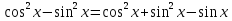
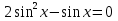
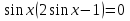
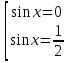
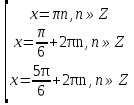
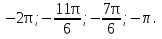
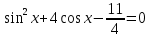
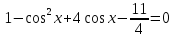
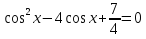
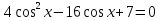
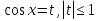
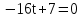
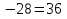
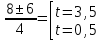
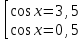
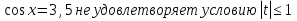
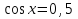
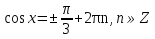
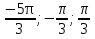
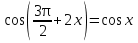 если x∊
если x∊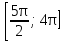 .
.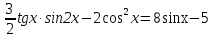 ,
, 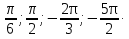
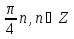 исключите те числа, которые принадлежат множеству X2={
исключите те числа, которые принадлежат множеству X2={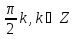 } и запишите получившееся числовое множество X.
} и запишите получившееся числовое множество X.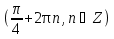 , В(
, В(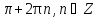 ), С(
), С(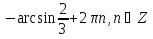 ).
).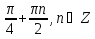 }.
}.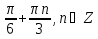 }.
}.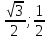 ), В(0;
), В(0;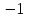 ), С(
), С(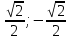 ).
).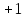 , если х∊
, если х∊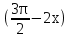 =sin x, если x∊
=sin x, если x∊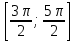 ;
;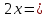 1
1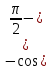 , если x∊
, если x∊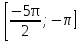 ;
;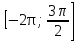 .
.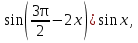 если х∊
если х∊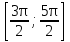
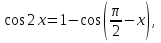 если х
если х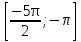
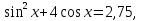 если x
если x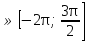
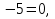 если x∊
если x∊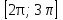 .
.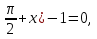 если x∊
если x∊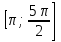 .
. [0; 2
[0; 2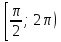 .
.