Разработка урока алгебры в 10 классе по теме «Тригонометрические уравнения»
 Скачать 61.27 Kb. Скачать 61.27 Kb.
|
| Разработка урока алгебры в 10 классе по теме «Тригонометрические уравнения» учителя математики Крапчатой И.А. Цели: дидактическая: овладеть навыками решения некоторых видов тригонометрических уравнений; развивающая: вариативность и успешность обучения на фоне открытости методической работы; воспитательная: нравственное воспитание учащихся, развитие коммуникативных умений, культуры и дисциплины умственного труда. Оборудование: Мультимедийная установка; задания на печатной основе; тетради для самостоятельных работ. Ход урока I. Организационный момент. Проверка готовности учащихся к уроку, запись домашнего задания и пояснение к нему. Сообщается тема урока. К доске вызываются 3 ученика, которые работают на доске по карточкам. II. Актуализация знаний, умений и навыков учащихся. а) Устная работа (задания показываются на экране с помощью мультимедийной установки) б) Фронтальная работа Учитель: Какие простейшие тригонометрические уравнения мы рассмотрели? Ученик: sin x = a, cos x = a, tg x = a, ctg x = а Учитель: Какова ориентировочная основа действий при решении уравнения sin x = а? Ученик Функция у = sin x возрастает на промежутке [– x = arcsin a. Арксинусом числа а называется число b, b Общий вид корней на области допустимых значений переменной х имеет вид: x = Частные случаи: sin x = 0; x = sin x = 1; x = sin x = – 1; x = – Учитель: Какова ориентировочная основа действий при решении уравнения cos x = а? Ученик: Функция у = cos x убывает на промежутке [о; x = arсcos a. Арккосинусом числа а называется число b, b Частные случаи: cos x = 1; x =2 cos x = 0; x = cos x = – 1; x = Учитель: Назовите формулу корней для решения уравнения tg x = a Ученик: : x = arctg a + Учитель: Назовите формулу корней для решения уравнения tg x = a Ученик: : x = arcctg a + в) Проверка учащихся, работающих у доски Ученик 1: Карточка №1 (уровень слабого учащегося) 1.Решить уравнение 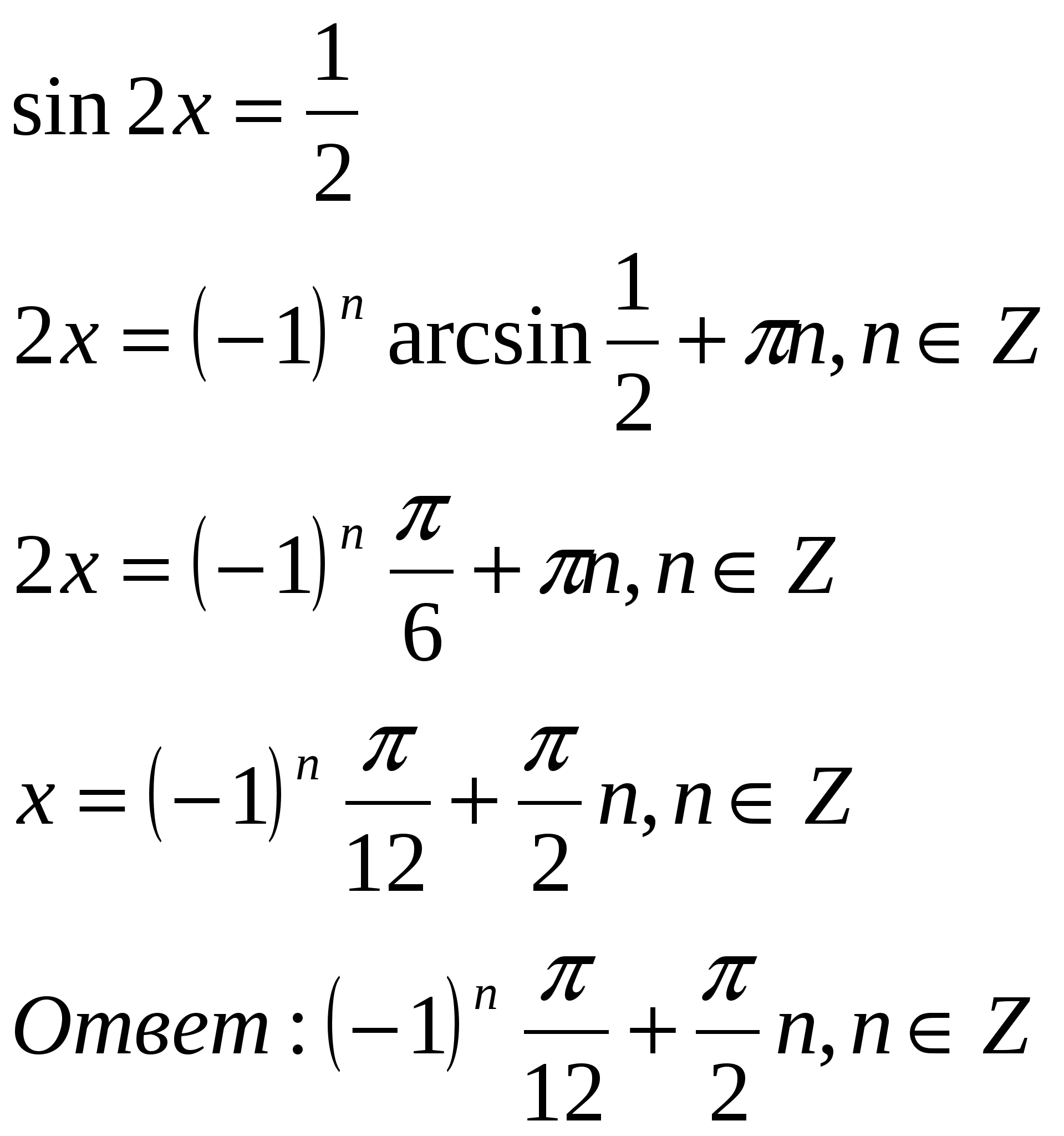 2. Решить уравнение 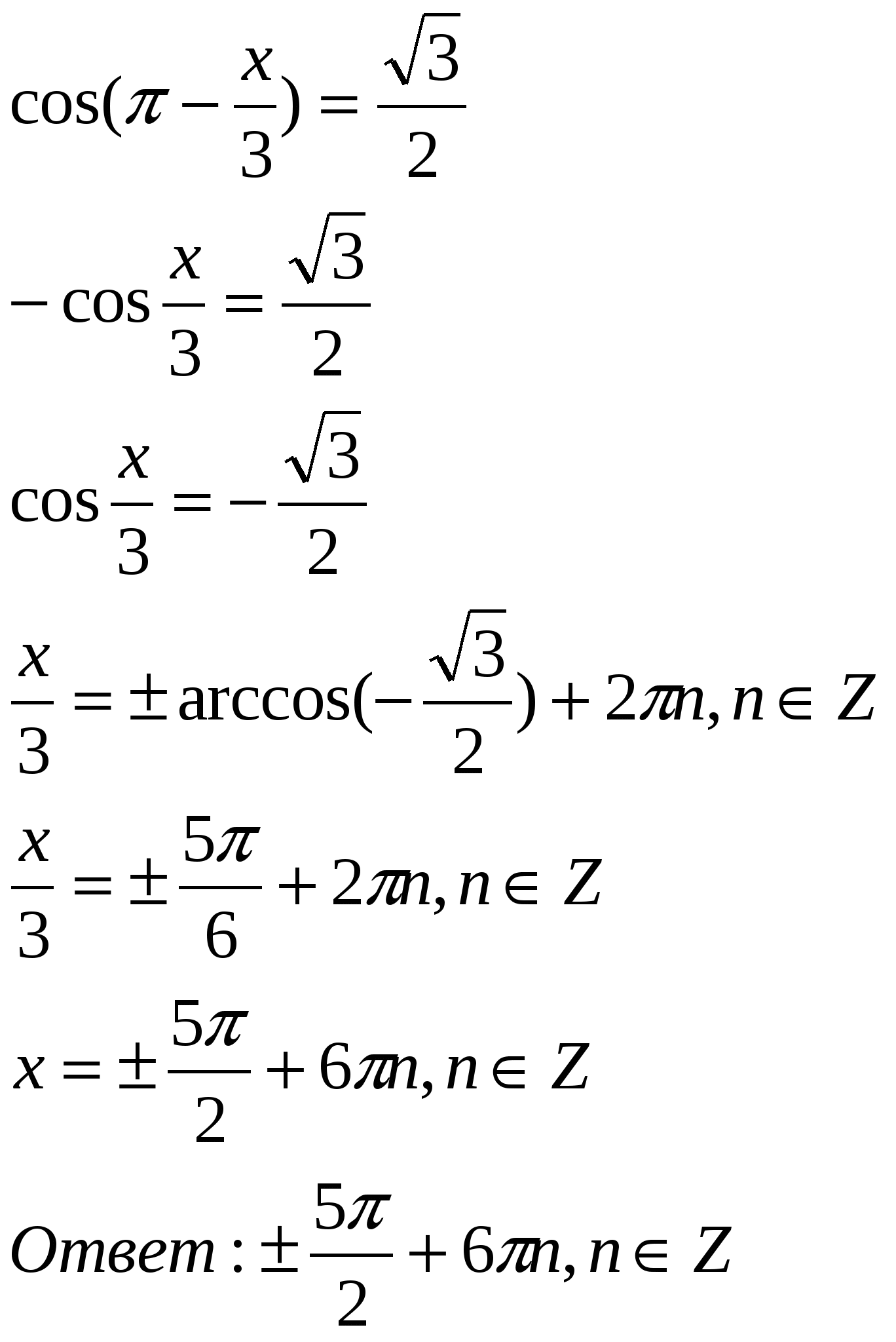 Ученик2: Карточка №2 (уровень среднего учащегося) 1. Решить уравнение  2. Решить уравнение  Ученик3: Карточка №3 (уровень сильного учащегося)
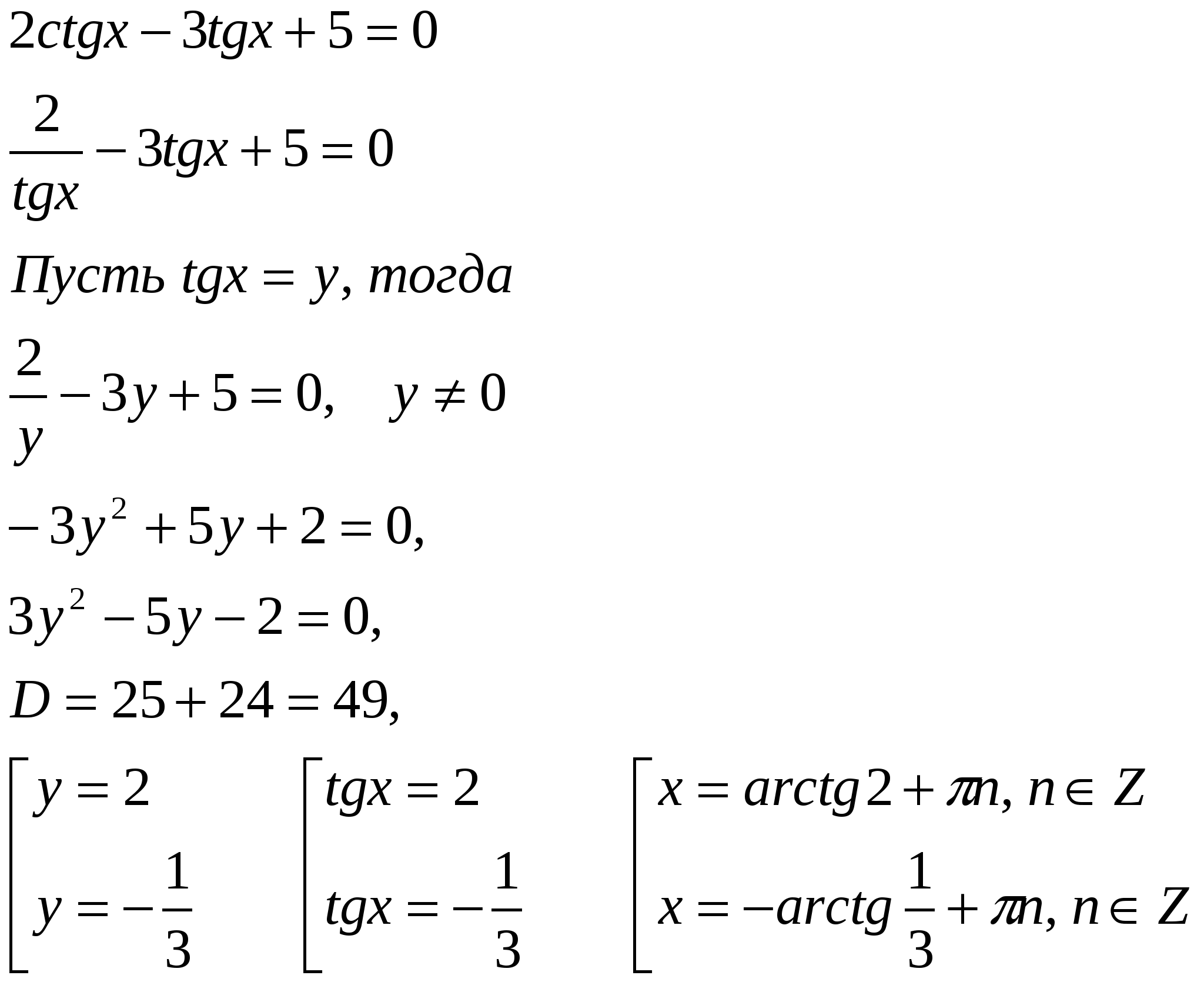 Ответ: 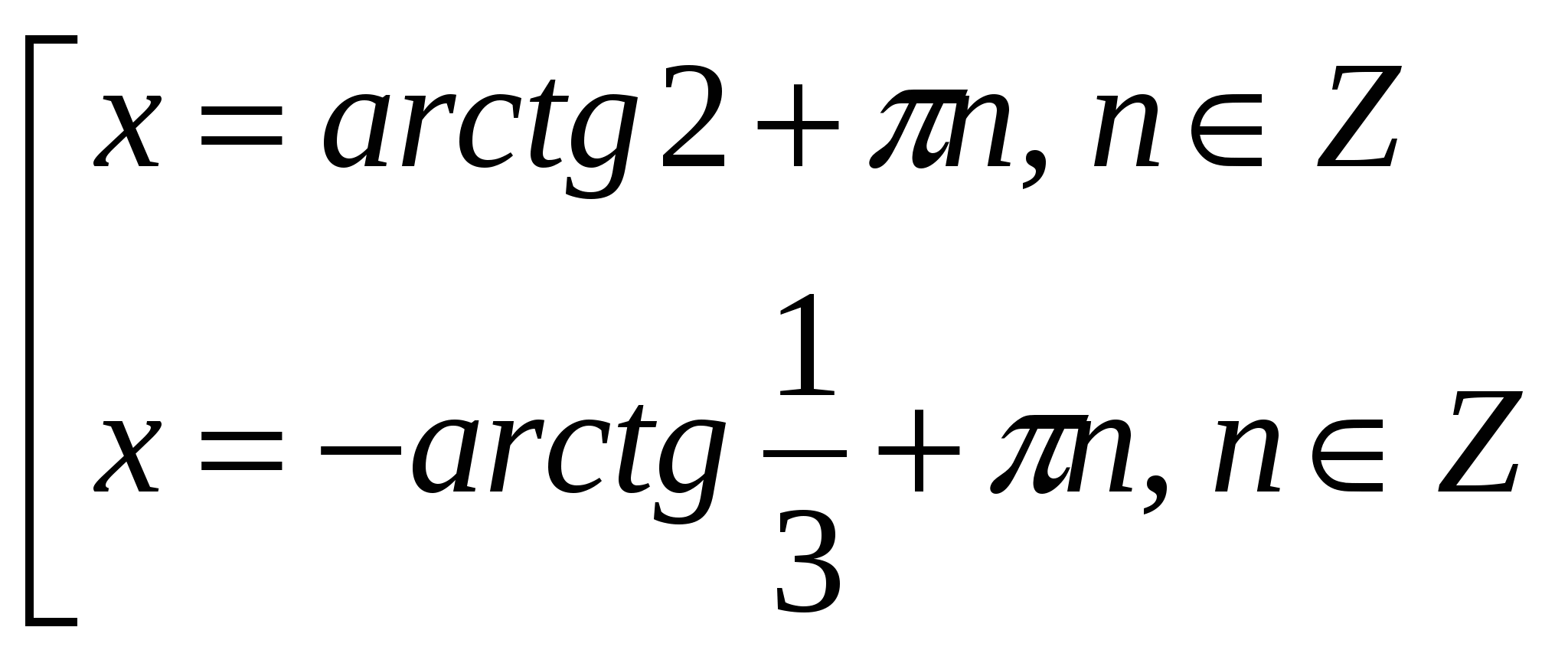
 III. Реализация целей урока. Учебная цель: овладеть навыками решения некоторых видов тригонометрических уравнений. Учитель: (на доске разбирает решение уравнений, учащиеся записывают их в тетрадях) 1. Решите уравнение: Решение: 1) данное уравнение равносильно: 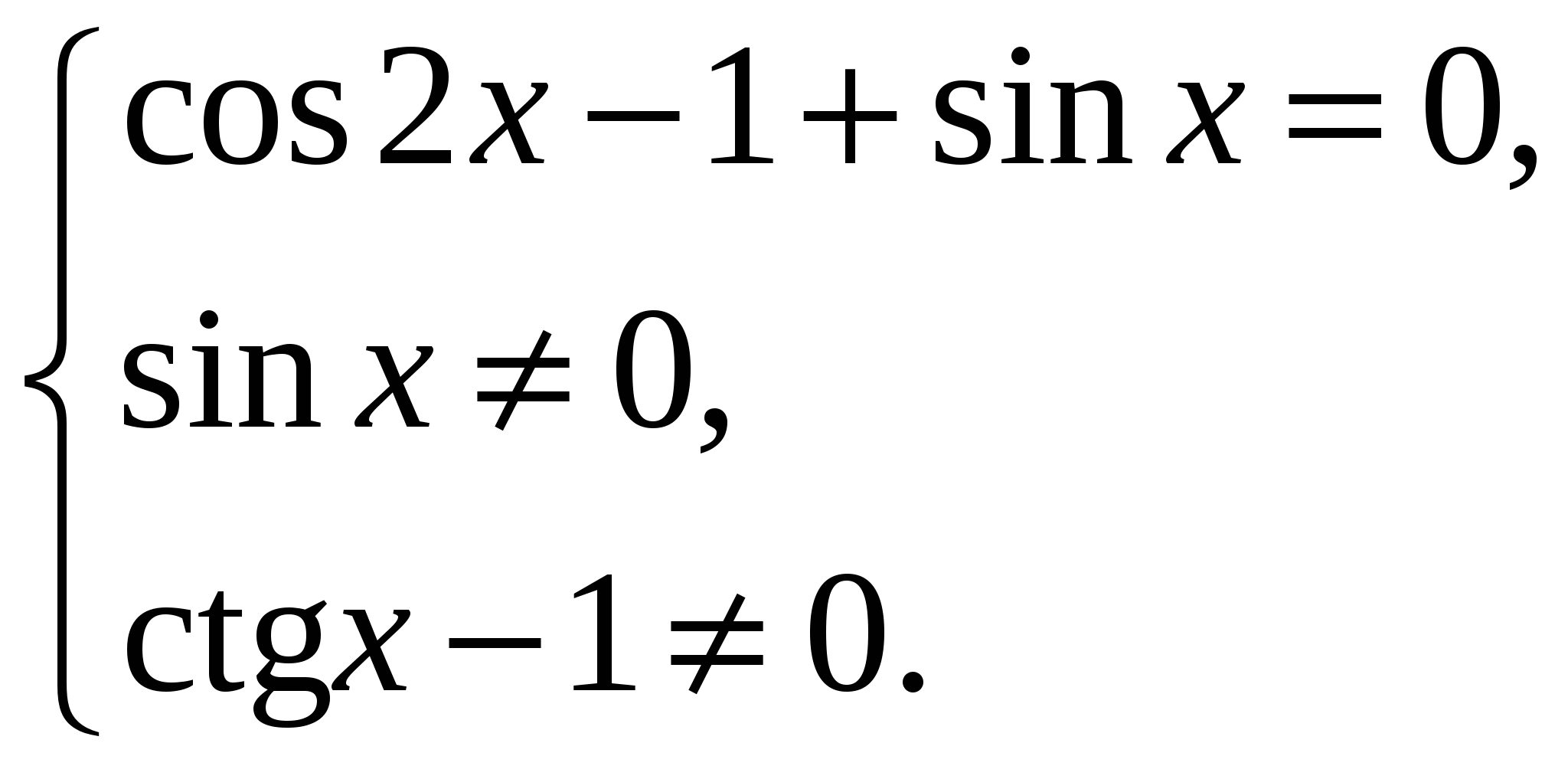 . .2) 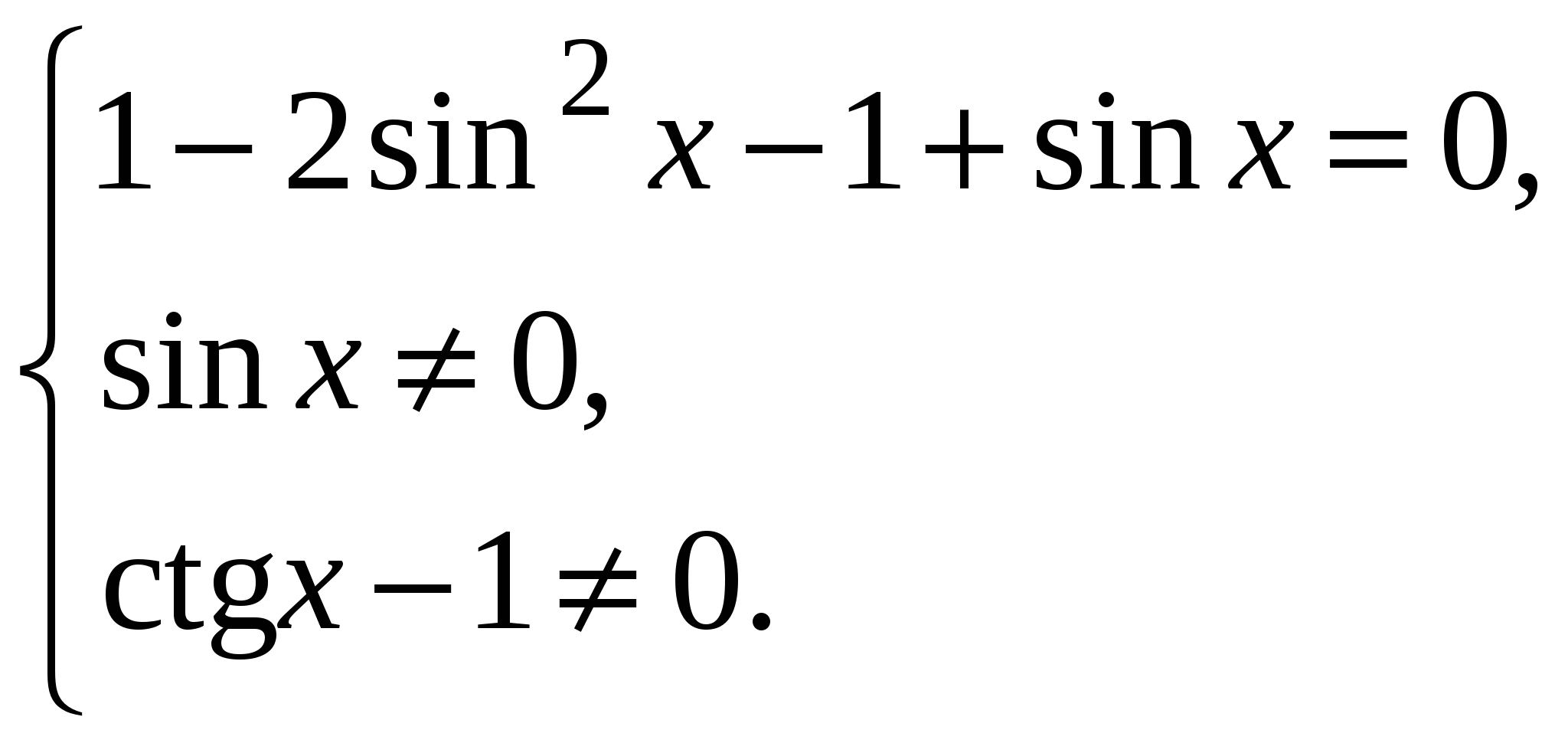  . . а) 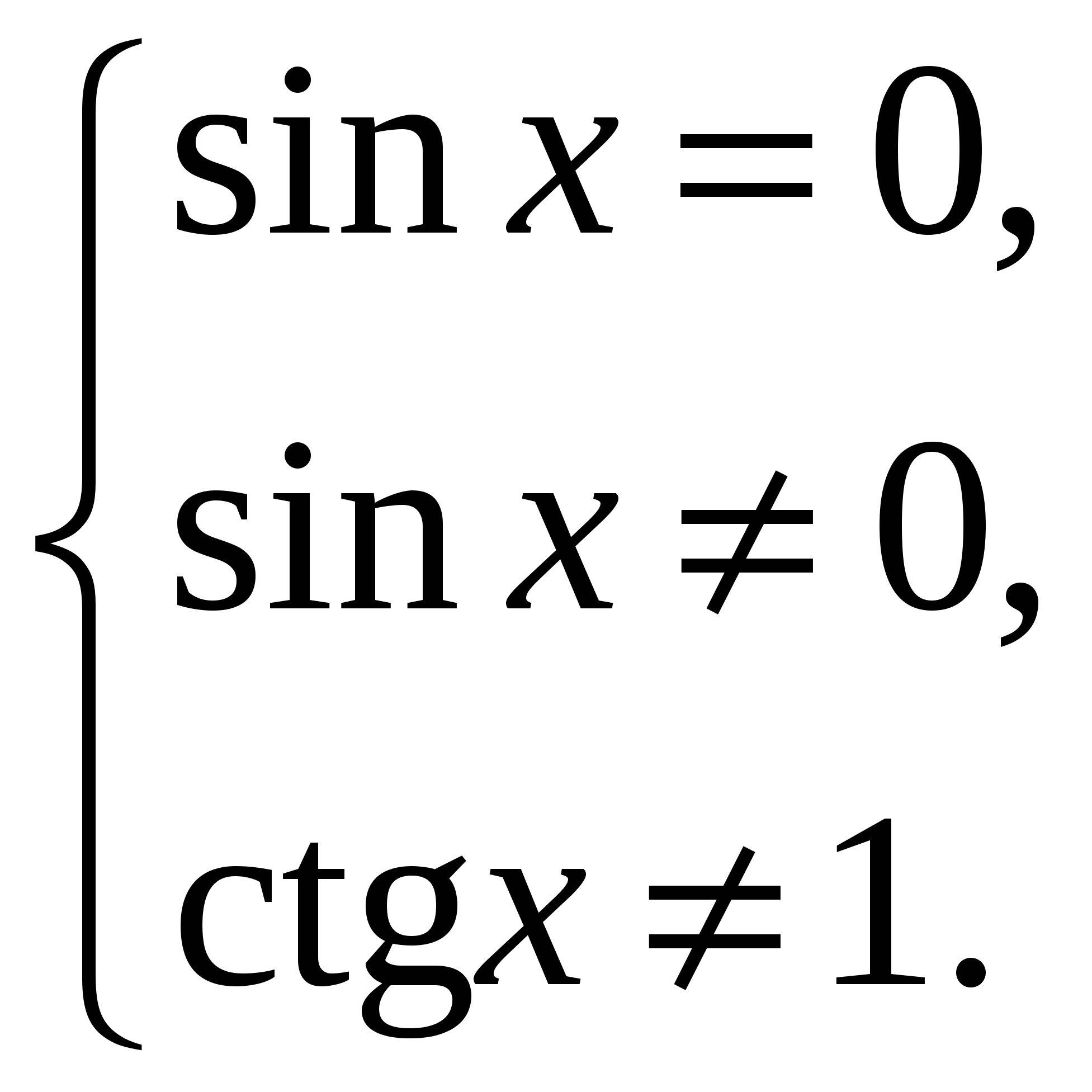 - не имеет решений, б) - не имеет решений, б) 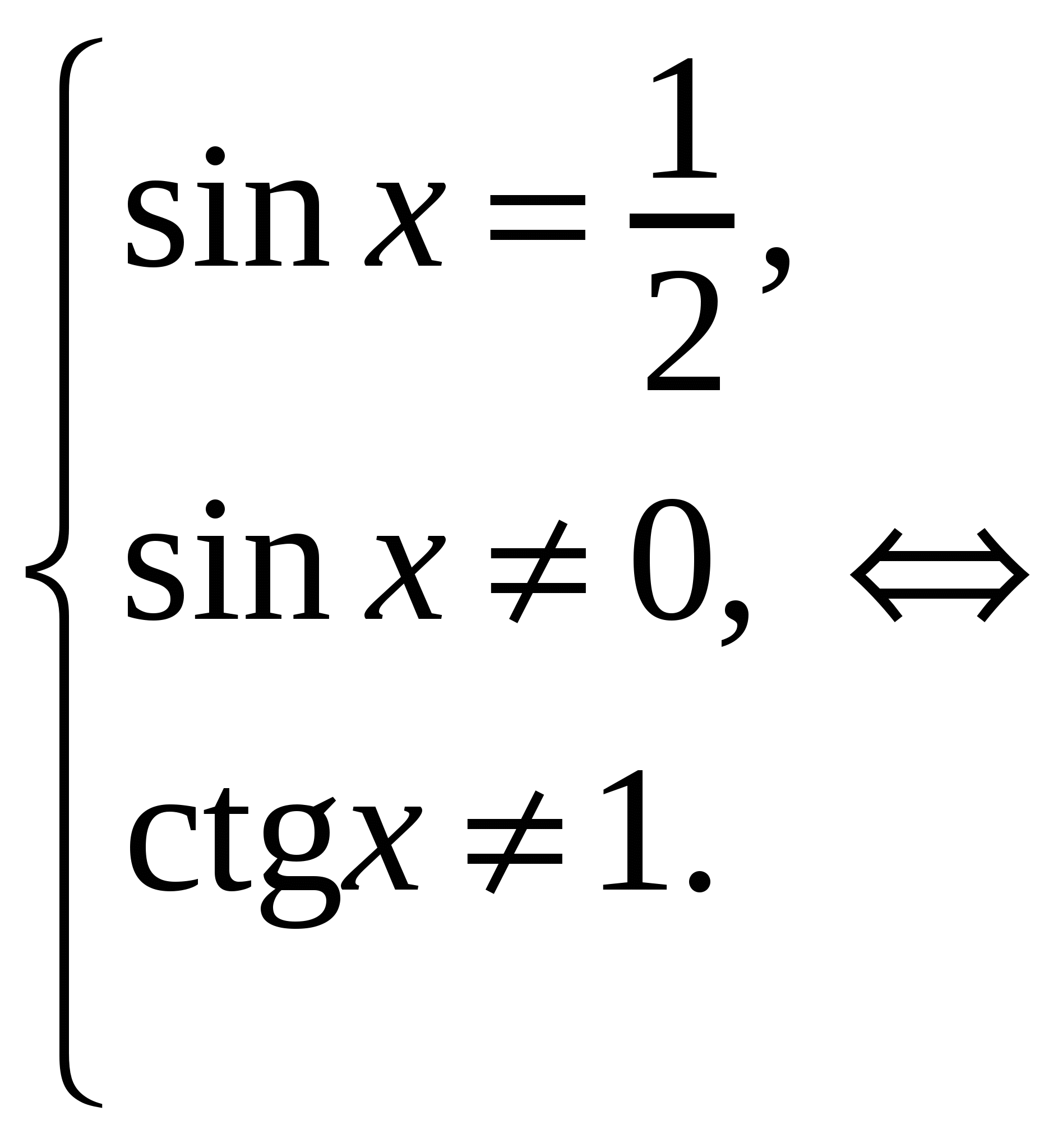 Ответ: 2. Решите уравнение Решение. 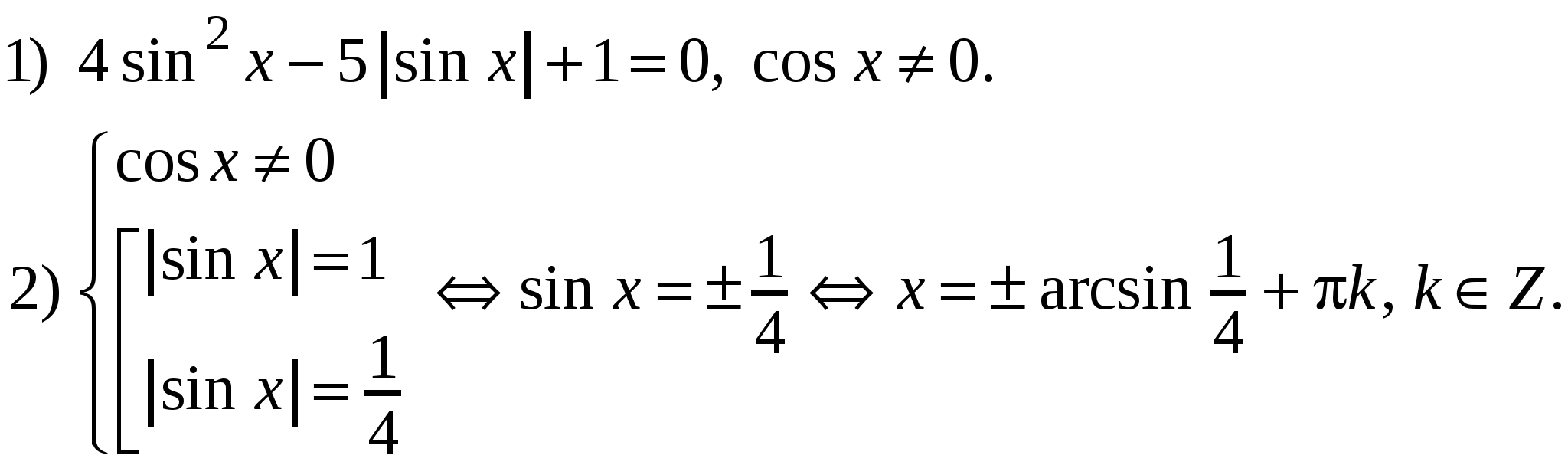 Ответ: IV. Самостоятельная работа по вариантам, задания на печатной основе. Вариант 1 (уровень слабого учащегося) А1. Решите уравнение
А2. Решите уравнение:
А3. Решите уравнение
А4. Решите уравнение:
А5. Решите уравнение
Вариант 2 (уровень слабого учащегося) А1. Решите уравнение
А2. Решите уравнение
А3. Решите уравнение
А4. Решите уравнение
А5. Решите уравнение
Вариант 3 (уровень среднего учащегося) А1. Решите уравнение
А2. Решите уравнение
В1 Решите уравнение: cos 2 x+3 sin x-3=0 Вариант 4 (уровень среднего учащегося) А1. Решите уравнение:
А2. Решите уравнение
В1 Решить уравнение: tg x-2 ctg x+1 = 0 Вариант 5 (уровень сильного учащегося) С1. Решите уравнение С2. Решите уравнение: Вариант 6 (уровень сильного учащегося) С1. Решите уравнение С2. Решите уравнение: 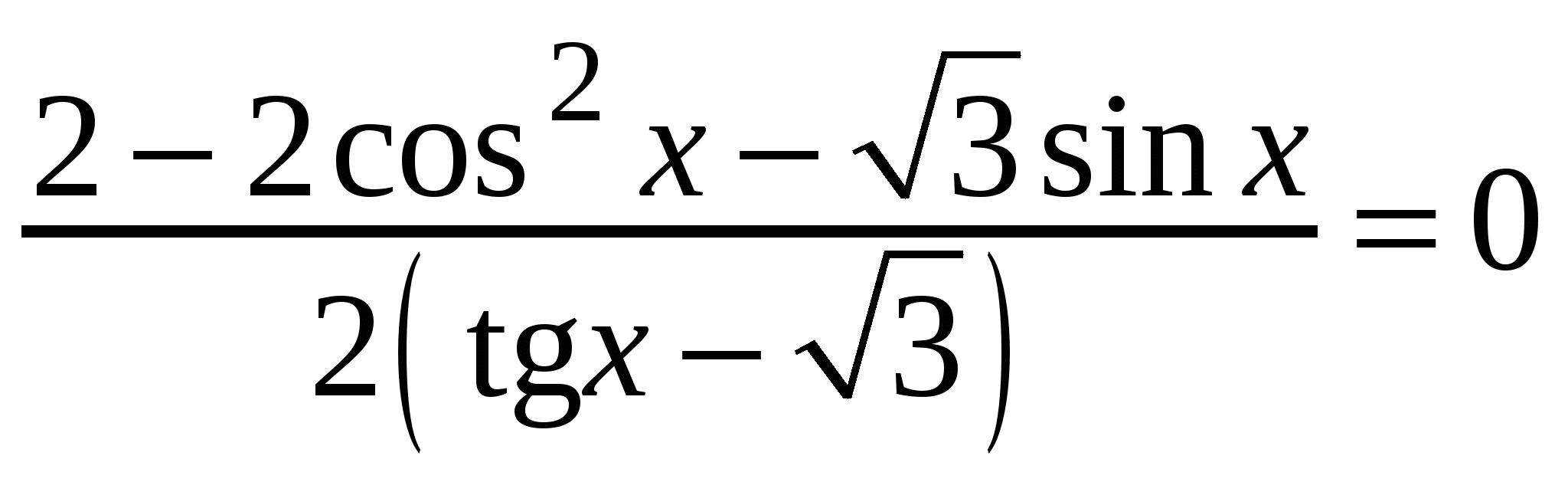 . .V. Подведение итога урока, выставление оценок. |