Организация самостоятельной работы учащихся на уроках математики

Название	Организация самостоятельной работы учащихся на уроках математики
Дата	05.04.2016
Размер	140.81 Kb.
Тип	Документы

Пьянзина Валентина Ивановна – учитель математики МБОУ «Большеигнатовская средняя общеобразовательная школа»
Тема «Организация самостоятельной работы учащихся на уроках математики».
« Знание только тогда знание,

когда оно приобретено усилием собственной мысли, а не памятью». Л.Н.Толстой

Организация самостоятельной работы – это ответственная и сложная работа учителя. Самостоятельная работа оказывает значительное влияние на глубину и прочность знаний учащихся, на развитие их познавательных способностей, на темп усвоения изученного материала.

Самостоятельную деятельность учащихся можно и нужно организовывать на различных уровнях: от воспроизведения действий по образцу и узнавания объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях. Учителю необходимо учитывать, что при составлении заданий для самостоятельной работы степень сложности должна отвечать учебным возможностям детей. Переход от одного уровня на другой должен осуществляться постепенно, когда учитель будет убежден, что учащийся справится со следующим уровнем самостоятельности. И очень важно, чтобы содержание самостоятельной работы и время ее выполнения отвечали основным целям обучения данной темы. Но злоупотребление самостоятельной работой также вредно, как и ее недооценка. Если включать в урок самостоятельную работу без особой необходимости, просто ради разнообразия, то в результате будет потрачено драгоценное время урока. Учитель должен тщательно продумать место и время самостоятельной работы, определить ее содержание, разбить задания по уровням сложности, поэтому учителю важно знать виды самостоятельных работ, их место в процессе обучения. Самостоятельные работы могут быть: 1) обучающимися, 2)тренировочными, 3)закрепляющими, 4)повторительными, 5)развивающими, 6)творческими, 7)контрольными.

Рассмотрим более подробно каждый из видов.
1. Обучающие самостоятельные работы. Смысл обучающихся самостоятельных работ заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ - развитие интереса к изучаемому материалу, привлечение каждого ученика к работе на уроке. При выполнении данного вида работ школьник сразу видит, что ему непонятно, и он может попросить дополнительно объяснить эту часть материала. Данный вид самостоятельных работ помогает выделить пробелы в знаниях прошлого материала у школьников. Самостоятельные работы по формированию знаний проводятся на этапе подготовки к введению нового содержания, также при непосредственном введении нового содержания, при первичном закреплении знаний, т.е. сразу после объяснения нового, когда знания учащихся еще не прочны. Учителю необходимо знать следующие особенности обучающих самостоятельных работ: составлять из заданий репродуктивного характера, проверять немедленно.
Так как самостоятельные обучающие работы проводятся во время объяснения нового материала или сразу после объяснения, то их немедленная проверка дает учителю четкую картину того, что происходит на уроке, какова степень понимания учащимися нового материала, на самом раннем этапе его обучения. Цель этих работ – не контроль, а обучение, поэтому им следует отводить достаточно времени на уроке. Проведение самостоятельной работы надо организовывать так, чтобы она не только обеспечивала восприятие программного материала, но и способствовала бы всестороннему развитию учащихся.

Пример 1. Тема « Свойства степени с натуральным показателем»

Самостоятельная работа.

Составить три примера на каждое свойство степени:

1). а

* а

= а

4). ( а в )

= а

2) а

: а

= а

5). (

)

, b

0.

3) ( а

)

= а

К обучающим самостоятельным работам можно отнести и самостоятельное составление алгоритмов, решение задач по алгоритму.

Пример 2. Для функции у(х) = х найти первообразную, график которой проходит через точку М(2;5).

Решение.

F(x) =

+C. Найдем число С, такое, чтобы график функции у =

+C проходил

через точку М( 2;5). Подставляя х = 2, у = 5, получим 5 =

+ С, откуда С = 3. Следовательно, F(x) =

+3.

АЛГОРИТМ. 1). Записать общий вид первообразной;

2). Подставить в полученную формулу координаты точки и рассмотреть уравнение относительно С;

3). Решить уравнение, найти С;

4). Записать значение С в формулу первообразной F(x) =

+C.

Пример 3. Тема «Свойство описанного четырехугольника»

ВАРИАНТ 1	ВАРИАНТ 2
1.В равносторонний треугольник вписана окружность радиусом 5см. Найти сторону треугольника.	1В равносторонний треугольник со стороной 6см вписана окружность. Найти радиус окружности.
2. Четырехугольник АВСД описан около окружности. Найти стороны АВ и СД, если ВС=8см, АД=10см, АВ в два раза больше СД.	2. Четырехугольник АВСД описан около окружности. Найти стороны ВС и АД, если АВ = 8см, СД=9см, ВС в два раза меньше АД.

2. Тренировочные самостоятельные работы. К ним относятся задания на распознавание различных объектов и свойств.
В тренировочных заданиях часто требуется воспроизвести или непосредственно применить теоремы, свойства тех или иных математических объектов и др.
Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Такая работа мало способствует умственному развитию детей, но она позволяет выработать основные умения и навыки, тем самым создать базу для дальнейшего изучения материала. При выполнении тренировочных самостоятельных работ необходима помощь учителя, также можно разрешить пользоваться учебником и записями в тетрадях, таблицами. Все это создает благоприятный климат для слабых учащихся. В таких условиях они легко включаются в работу и выполняют её. В тренировочные самостоятельные работы можно включить выполнение заданий по разноуровневым карточкам.

Пример. Тема « Свойства степени с натуральным показателем»

Вариант 1 (на «3»)	Вариант 2 (на «4»)	Вариант 3 (на «5»)
1. Упростите выражение: a) ; б) ; в) ; г) ; д) . 2. Вычислить: а) ; б) . 3. Записать в стандартном виде 1230000.	1. Представить в виде степени с основанием 2: а) 16; б) 8⁵; в) (16²)³; с основанием 5: а) 125; б) 25⁴. 2. Вычислить: а) ; б) . 3. Упростить: .	1. Вычислить: а) ; б) . 2. При каком значении n верно равенство: а) ; б) . 3. Вычислить: .

3. Закрепляющие самостоятельные работы. К ним можно отнести самостоятельные работы, которые способствуют развитию

логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно усвоен учебный материал. По результатам проверки заданий данного вида учитель определяет, нужно ли еще заниматься данной темой. Примеры. Тема урока « Свойство вписанного четырехугольника»

ВАРИАНТ 1	ВАРИАНТ 2
1. Равносторонний треугольник АВС вписан в окружность радиуса 4см. Найти его сторону.	1. Равносторонний треугольник МКС со стороной 6см вписан в окружность. Найти его радиус.
2. Прямоугольный треугольник с катетами 6см и 8см вписан в окружность. Найти его радиус.	2. Прямоугольный треугольник вписан в окружность радиуса 6,5см. Найти площадь треугольника, если один катет равен 5см.

4. Повторительные (обзорные или тематические) самостоятельные работы.

Они проводятся перед изучением новой темы, во время которых

учитель выясняет, подготовлены ли школьники, какие у них знания, какие проблемы могут затруднить изучение нового материала.

Пример. Тема урока «Разложение квадратного трехчлена на множители»

ВАРИАНТ 1	ВАРИАНТ 2
1.Разложить многочлен на множители:	1. Разложить многочлен на множители:
а) 3х+2х-5, в) 2х+5ху -7у, с) х- (5а+1)х +6а+а-2.	а) 7х -5х -2, в) 3х+5ху -8у, с) х- ( 5а+1)х +6а+5а-6.
2. СОКРАТИТЬ ДРОБЬ:	2.СОКРАТИТЬ ДРОБЬ:
а) , в)	а), в)

5. Самостоятельные работы развивающего характера.

Здесь можно дать задания на составление докладов, на подготовку к олимпиадам, научно творческим конференциям, проектам, на проведение в школе недели математики. На уроках можно включать задачи исследовательского характера

Примерная тематика проектов.

1	Темы проектных работ по математике для учащихся 5 класса
	Когда возникли натуральные числа, первые обозначения, разряды , классы. Мера длины в разных странах, сравнение с мерой длины в России. Единицы измерения площадей (объемов), когда возникла метрическая система мер. Почему возникла необходимость введения обыкновенных дробей. История возникновения десятичных дробей. Где, когда, зачем ввели проценты?
2	Темы проектных работ по алгебре для учащихся 7 класса
	История возникновения уравнений , решения каких уравнений дошли до наших дней? Как возникли формулы сокращенного умножения, какие формулы дошли и применяются в школьном курсе, а какие не применяются?
3	Темы проектных работ по геометрии для учащихся 7 класса
	История возникновения планиметрии, основные фигуры. Что такое признаки, кто ввел, как использовались прямоугольные треугольники в древности, связь признаков Кто открыл сумму углов треугольника, какие версии существовали в планиметрии?

6. Творческие самостоятельные работы, которые предполагают достаточно высокий уровень самостоятельности. Здесь можно включать и задачи на поиск нескольких способов решения.

Пример. Тема урока « Свойства и графики основных функций»

Вариант 1	Вариант 2
1. Построить графики функций:	1. Построить графики функций:
1) у = х + 2) y = + 3) y = 2x+1 +.	1) у = 2 х + 2) y = - 3) y= 2x+1 - .
2. Построить множество точек, координаты которых удовлетворяют условию:	2. Построить множество точек, координаты которых удовлетворяют условию:
1) = x-3, 2) +=1, 3) y x+2.	1) =2 x-3, 2) +=3, 3) y x+4.

7. Контрольные самостоятельные работы. Они выполняют функцию контроля. Контрольные задания должны быть равноценными по содержанию и объему работы; они должны быть направлены на отработку основных навыков; обеспечивать достоверную проверку уровня знаний.

Пример. Тема « Уравнения и системы неравенств».

ВАРИАНТ 1	ВАРИАНТ 2
1. Решить уравнение:	1. Решить уравнение:
А) , В) (3х -2) ( х-1) = 4( х-1)	А) , В) ( 2х-1) (х-2) = 5( х-2)
2. Решить систему уравнений:	2. . Решить систему уравнений:
;	;
3. Решить систему неравенств:	3. Решить систему неравенств:

Эффективность самостоятельной работы, формирование навыков самостоятельной деятельности во многом зависит от своевременного анализа результатов работы, когда у ученика еще не окончен процесс корректировки собственных знаний. Анализ самостоятельной работы должен носить обучающий характер, т.е. учитель должен не просто констатировать количество ошибок, а проводить их разбор, с тем, чтобы учащиеся смогли до конца понять вопросы, в которых сделали ошибки.

Опыт показывает, что систематически проводимая самостоятельная работа при правильной ее организации способствует получению учащимися более прочных знаний .Самостоятельная работа важнейшее условие саморегуляции личности, ее творческих возможностей. Самостоятельная работа ученика - главный путь воспитания самостоятельности. Но самостоятельная работа, привлекая современных школьников, вызывает в тоже время у многих серьезные затруднения. Она требует эмоционального и умственного напряжения, порождает массу неожиданных вопросов и ошибок, сомнения и переживания. Замечено, что особенно много затруднений возникает у ребят на начальном этапе выработки тех или иных умений и навыков, поэтому начинать эту работу надо в начальных классах. В своей работе я хочу осветить вопросы о правильности организации самостоятельной работы, так как я считаю, что самостоятельная работа служит эффективным средством формирования личности, побуждает умственную самостоятельность у детей. Она дисциплинирует мысль, рождает у школьников веру в себя, в свои силы и возможности. В процессе обучения математике задача учителя состоит не только в том, чтобы обеспечивать прочные знания, предусмотренные программой, но и в том, чтобы развивать самостоятельность и активность мышления учащихся. Самостоятельная работа - это такая познавательная учебная деятельность, когда последовательность мышления ученика, его умственные и практические операции и действия зависят и определяются самим учеником. Присутствие самостоятельной работы необходимо на уроках, в том числе и на уроках математики, так как они тренируют волю, воспитывают работоспособность, внимание, дисциплинируют учащихся. Учителю на уроках математики необходимо опираться на самостоятельную работу учеников, самостоятельное рассуждение, умозаключение. Самостоятельная работа - это метод, который очень помогает учителю для выяснения способностей учащихся. Работая самостоятельно, ученик должен постепенно овладеть такими общими приемами самостоятельной работы как ясное представление цели работы ее выполнение, проверка, исправление ошибок. При правильной методике организации проведения самостоятельных работ активизируется умственная деятельность детей. Если детям прививать навыки выполнения самостоятельной работы и использовать на уроках различные ее виды, то у детей вырабатывается самостоятельность и развивается мышление, они стремятся выполнять более трудные задания. В самостоятельной работе детей большое место занимает репродуктивная деятельность. Обязательным условием является индивидуализация самостоятельных заданий, то есть их посильность, учет меры сложности для каждого ребенка или группы детей, имеющих почти одинаковый уровень развития. Сформировать у детей необходимые навыки учебной деятельности позволяет умелое сочетание индивидуальной, групповой, фронтальной работы. Выбор формы работы зависит от цели, сложности заданий, уровня сформированности учебной деятельности и возможностей каждого ребенка. Если задание простое и посильно для всех, оно дается всей группе, и каждый выполняет его самостоятельно. Для индивидуальной самостоятельной работы должны быть подготовлены специальные дидактические пособия. Они должны содержат задания разной трудности. Традиционно самостоятельная работа рассматривается как индивидуальная познавательная деятельность ученика. Работая самостоятельно, ученик продвигается своим темпом, не связан с классом. При анализе общей структуры темы, учитель заранее определяет для себя: какие вопросы учащиеся могут усвоить самостоятельно, какие задания будут предложены с целью формирования обще-учебных умений, задания репродуктивного и творческого характера, направленные на развитие специальных умений, индивидуальных особенностей учащихся, формы организации коллективной самостоятельной деятельности на уроках математики (работа в парах). В тематическом плане важно отметить логическую последовательность работ, их разнообразие и усложнение. Второй этап планирования самостоятельной работы на уроках математики связан с подготовкой учителя к конкретным урокам. Важно продумать организацию, методическую инструментовку в зависимости от педагогической ситуации и особенности класса. Поэтому в поурочном плане учителя могут указать: место самостоятельной работы. В структуре урока; задания (их направленность и содержание); время, выделяемое для выполнения заданий. В начале урока оправданы непродолжительные работы, рассчитанные на 5-10 мин. чтобы включить весь класс в активную деятельность, мобилизовать внимание, память, мышление учащихся, создать рабочий настрой. Предлагая задания, аналогичные тем, которые учащиеся выполняли дома, учитель имеет возможность убедиться, кто из ребят справляется с заданием самостоятельно, кто допускает ошибки, затрудняется. Наряду с этим выясняется готовность класса к усвоению нового материала, к выполнению более сложных заданий. Такого рода самостоятельные работы носят и проверочный характер, так как направлены на выявление и актуализацию опорных знаний и умений, что служит подготовкой к усвоению нового материала. Дифференцированный подход к учащимся при планировании содержания и объема самостоятельной работы на уроках математики — один из возможных путей устранения перегрузки. Основная цель обучения - научить каждого ученика самостоятельно добывать знания, формировать навыки. Известно, что каждый ученик усваивает знания в зависимости от своих умственных способностей, памяти, темперамента, навыков учебного труда. Так как уровень знаний, познавательных способностей не у всех детей одинаковый, то на уроках при коллективной форме работы необходим дифференцированный подход в подборе заданий ( зачет в группах (работа в группах по теме производная)). Упражнения должны отличаться простотой, краткостью математического языка. Начинать работу следует с более простых упражнений, постепенно продвигаясь к более сложному (на этом этапе очень хорошо применять карточки- консультанты)

Учет индивидуальных особенностей учащихся в обучении, являясь общим дидактическим принципом, распространяется на работу по подготовке учащихся к самообразованию. Одним из эффективных путей учета в обучении индивидуальных различий является дифференцированный подход. Он важен и в плане развития познавательной самостоятельности и формирования у учащихся стремления к самообразованию. Дифференцированный подход предлагает мысленную разбивку учащихся на группы с учетом максимальных познавательных возможностей каждого. Наиболее часто используется отнесение учащихся к тем или иным группам, с учетом их образовательной подготовленности (сильные, средние, слабые). Но это не исключает группировку учащихся и по другим признакам. Дифференцированный подход к обучению означает, что учащимся дают задания различного уровня трудности. Причем самый низкий по трудности уровень соответствует требованиям учебной программы. Следует сказать о том, что дифференцированный подход сочетается с индивидуальным. Дифференцированные задания должны быть подготовлены к уроку заранее: записаны на доске, таблицах, карточках. Они содержат задания разной сложности. Особое внимание необходимо уделить развитию познавательного интереса к предмету, проведение творческих самостоятельных работ (сказки, кроссворды, биографии, различные доказательства одной и той же теоремы, поиски математически-исторических справок, подготовка докладов и презентаций) они требуют особой подготовки самого учителя. Жизнь человека — это движение по пути познания. Каждый шаг может обогащать нас, если благодаря новому мы начинаем видеть то, чего ранее не замечали или не понимали , чему не придавали значение. Уроки математики позволяют более правильно воспринимать окружающий мир, постигать истину, укреплять здравый смысл, находить свое место в мире, выбирать стиль поведения. Как будет вести себя человек, столкнувшись с незнакомым, неизведанным и непонятным? Один обойдет стороной, другой понаблюдает издалека, а кто-то попробует проникнуть в глубину и разобраться. Вот тут-то ему и пригодятся воля, навыки, мужество и самостоятельность. Чтобы дойти до конца. Чтобы найти выход. И если мои ученики дойдут до конца, значит, в этом есть и моя заслуга.
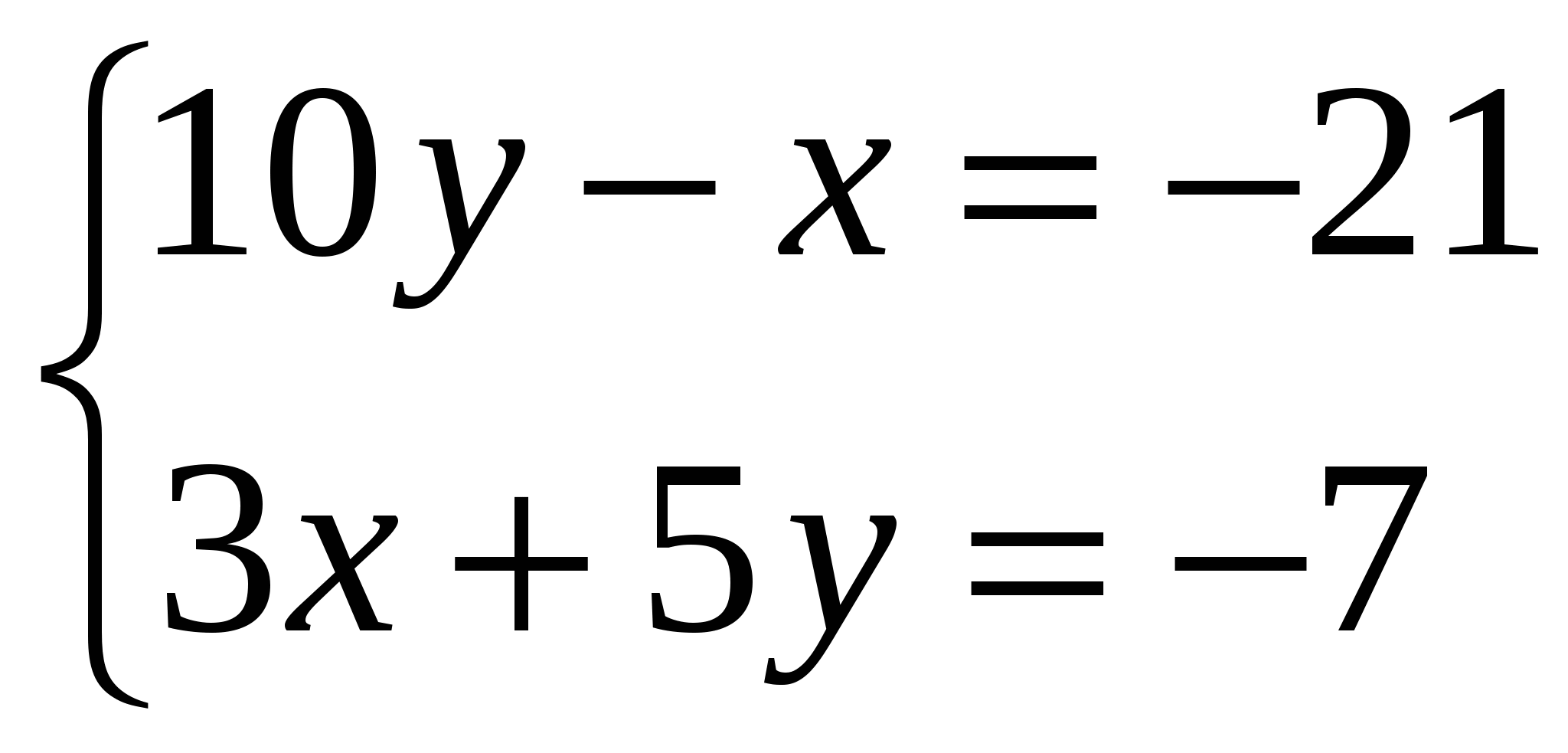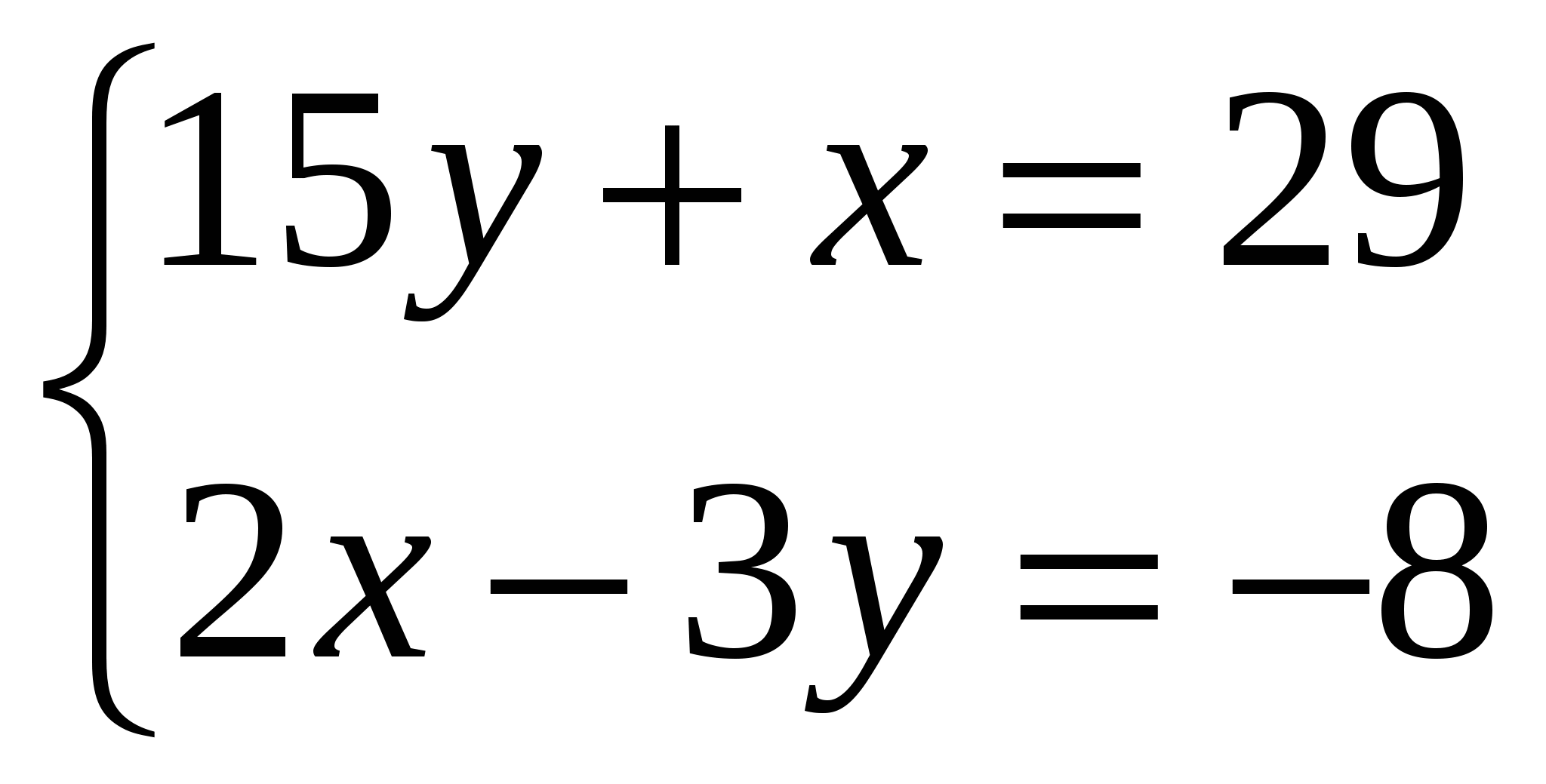