Самостоятельная работа учащихся на уроках математики в процессе личностно ориентированного обучения в современной школе
 Скачать 142.04 Kb. Скачать 142.04 Kb.
|
«Самостоятельная работа учащихся на уроках математики в процессе личностно ориентированного обучения в современной школе»Из опыта работы Н.В. Кириенко "Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью", – эти слова Л.Н. Толстого должны стать смыслом работы учителя. В процессе учения ученик участвует во многих различных видах деятельности, объективно направленных на осуществление целей обучения математике. Замечу, что если его деятельность объективно не направлена на осуществление этих целей, то говорят, что "ученик не учится", хотя и присутствует в классе. Этот случай рассматривать не будем. Будем предполагать, что хотя бы объективно все виды деятельности, которые реализует ученик, в той или иной степени направлены на осуществление целей обучения. Самостоятельную деятельность учащихся можно и нужно организовывать на различных уровнях: от воспроизведения действий по образцу узнавания объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях. Учителю необходимо учитывать, что при составлении заданий для самостоятельной работы степень сложности должна отвечать учебным возможностям детей. Переход с одного уровня на другой должен осуществляться постепенно, только когда учитель будет убежден, что учащийся справится со следующим уровнем самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают пробелы в знаниях. Очень важно, чтобы содержание самостоятельной работы, форма и время ее выполнения отвечали основным целям обучения данной теме на данном этапе. В то же время учителю нужно знать, что злоупотребление самостоятельной работой в учебном процессе также вредно, как и ее недооценка. Бывает так, что учитель включает в урок самостоятельную работу без особой необходимости, просто ради разнообразия, не продумав ее содержание и форму организации. Результаты бывают плачевны: или дети не готовы выполнить задание, или не хватило времени и т. п. А в результате – зря потрачено драгоценное время урока. Но если, составляя план урока, учитель тщательно продумал место и время самостоятельной работы, четко определил ее общее содержание, разбил задание по разным уровням сложности, то она сыграла свою положительную роль. В зависимости от целей, которые ставятся перед самостоятельными работами, они могут быть:
I. Смысл обучающих самостоятельных работ заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ – развитие интереса к изучаемому материалу, привлечение внимания каждого ученика к тому, что объясняет учитель. Здесь сразу выясняется непонятное, выявляются сложные моменты, дают себя знать пробелы в знаниях, которые мешают прочно усвоить изучаемый материал. Самостоятельные работы по формированию знаний проводятся при непосредственном введении нового содержания, при первичном закреплении знаний, т. е. сразу после объяснения нового, когда знания учащихся еще непрочны. Учителю необходимо знать следующие особенности обучающих самостоятельных работ: их надо составлять в основном из заданий репродуктивного характера, проверять немедленно и не ставить за них плохих оценок. Так как самостоятельные обучающие работы проводятся во время объяснения нового материала или сразу после объяснения, то их немедленная проверка дает учителю четкую картину того, что происходит на уроке, какова степень понимания учащимися нового материала на самом раннем этапе его изучения. Цель этих работ – не контроль, а обучение, поэтому им следует отводить много времени на уроке. При изучении темы "Логарифмы и их свойства" в классе после объяснений учителя можно предложить следующую самостоятельную работу: "Составьте по 2–3 примера, иллюстрирующих свойства логарифмов". Оформление работы может быть таким:  Конечно, не все учащиеся сразу найдут примеры с отрицательными числами, не все смогут оформить задания так, как показано в правом столбце, но, рассмотрев примеры учащихся, учитель сумеет направить их по нужному пути, одновременно продемонстрировав выражение целого числа через логарифм, подчеркнув, что такая запись нова только по виду ибо учащиеся давно умеют изображать одно и то же число в разных вариантах. Самостоятельно составляя примеры на изученные правила и свойства, учащиеся осмысленно их запоминают, учатся применять их, с интересом воспринимают изучаемый материал, так как они сами участвуют в его объяснении. К обучающим самостоятельным работам относятся так же самостоятельное составление алгоритмов, решение задач по алгоритму. Так в 6-м классе после изучения темы "Нахождение дроби от числа" предлагаю ребятам составить план (алгоритм) решения задач на нахождение процентов от числа. Вот что у них получается:
К старшим классам у ребят не возникает затруднений по составлению алгоритмов. Например, после того, как выведена формула первообразной, проходящей через данную точку, составляется следующий алгоритм:
II. К тренировочным относятся задания на распознавание различных объектов и их свойств. Например: среди функций, заданных формулами у = х + 0,5, у = – 0,5х + 4, у = 5х – 1, у = 0,5х + 1, у = 0,5х, выделить те, графики, которые параллельны графику функции у = 0,5х + 4. В тренировочных заданиях часто требуется воспроизвести или непосредственно применить теоремы, определения, свойства тех или иных математических объектов и др. Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Конечно, эта работа мало способствует умственному развитию детей, но она необходима, так как позволяет выработать основные умения и навыки и тем самым создать базу для дальнейшего изучения математики. При выполнении тренировочных самостоятельных работ учащимся (особенно слабым) еще необходима помощь учителя. Можно разрешить пользоваться и учебником, и записями в тетрадях, таблицами и т.п. Все это создает благоприятный климат для слабых учащихся. В таких условиях они очень легко включаются в работу и выполняют ее. К таким работам я отношу работы по обучающим карточкам. Такая карточка состоит из чередования трех блоков: 1 – опорная формула, написанная цветными чернилами; 2 – решенные примеры; 3 – Р. С. – реши сам. Приведу содержание двух карточек на тему "Действия со степенями" из курса алгебры 7-го класса.  К тренировочным самостоятельным работам можно отнести выполнение заданий по разноуровневым карточкам. Сейчас такие дидактические материалы выпущены и по алгебре, и по геометрии для всех классов. К этому виду работ я отношу работу учащихся по заполнению пропусков. После изучения темы "Умножение десятичных дробей" можно предложить такую работу. А. Чтобы найти произведение двух десятичных дробей, нужно: 1) выполнить ..., не обращая внимания на ..., 2) отделить ..., столько цифр ..., сколько их стоит после запятой вместе.... 3) если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут .... В. 1. Найдем произведение чисел 6, 42 и 30,5 1) Перемножим, не обращая внимания на запятые 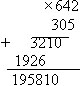 2) После запятой в обоих множителях ... цифр 3) Отделим запятой справа ... цифры 4) Получим 195,81. 2. Найти произведение чисел
Буквой А обозначены теоретические сведения. Если материал хорошо понят, то ребята заполняют пропуски очень быстро. Если же возникают проблемы, то заставляю еще раз читать текст пункта, помогаю разобраться в нем. Буквой В обозначены задания, закрепляющие теорию. Очень большую пользу приносят тренировочные самостоятельные работы с практической направленностью по геометрии. При выполнении таких работ учащиеся пользуются учебниками, справочной литературой, таблицами, что способствует развитию навыков самостоятельности, их подготовке к самообразованию. III. K закрепляющим можно отнести самостоятельные работы, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно, осмыслено усвоен учебный материал. По результатам проверки заданий данного вида учитель определяет, нужно ли еще заниматься данной темой. Работы предлагаю трех видов: - работа, состоящая из заданий по принципу «от простого к сложному», - работа с выделением упражнений обязательного уровня и упражнений дополнительной части; - работа, содержащая задания только одного уровня. Считаю, что контроль знаний с использованием дифференцированных заданий имеет ряд преимуществ, во – первых, у учащихся появляется право выбора, во – вторых, выполнив работу, ученик знает, какую отметку он получит за тот или иной уровень, в – третьих, ответственность за выбор ложиться на ученика, т.е. он сам выбирает задания того уровня, какой будет выполнять, соответственно он отвечает за отметку, которую получит. В своей работе очень часто применяю дифференцированные домашние задания. Это помогает решать две задачи: предупредить перегрузку учащихся и позволяет развивать интерес у тех ребят, для которых домашние задания слишком легкие. В классе, как правило, есть "сильные", "средние" и "слабые" ученики, поэтому для контроля усвоения какой-либо темы предлагается работа по индивидуальным карточкам. Она, с одной стороны, является контролем-диагностикой, с другой – выполняет развивающую функцию. Но самое главное – работа по карточкам позволяет установить обратную связь: ученик в ходе выполнения задания может задавать вопросы учителю. Результаты такой работы позволяют учителю делать выводы о достижении базового уровня знаний каждым учеником класса на данном этапе изучения того или иного материала  При изучении курса геометрии в 7 – 9-х классах перед учащимися ставятся задачи проводить доказательные рассуждения и устанавливать зависимости между элементами фигуры. Задача проводить доказательные рассуждения дифференцируется для разных групп учащихся: для сильных – проводить, для средних – воспроизводить, а для слабых – видеть ситуацию. Поэтому карточка должна включать, по крайней мере, два задания:
Карточка А рекомендуется для учащихся, не достигающих уровня обязательной подготовки:
Карточка Б рекомендуется для учащихся, достигающих уровня обязательной подготовки:
Карточка В рекомендуется для учащихся, достигающих продвинутого уровня подготовки.
Примеры карточек по теме "Равнобедренный треугольник": А.
Б.
В.
IV. Очень важны так называемые повторительные (обзорные или тематические) работы. Перед изучением новой темы учитель должен знать, подготовлены ли школьники, есть ли у них необходимые знания, какие пробелы смогут затруднить изучение нового материала. Например, в курсе алгебры и начал анализа 11-го класса перед изучением  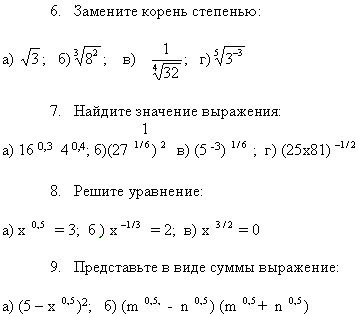 IV. Самостоятельными работами развивающего характера могут быть домашние задания по составлению докладов на определенные темы, подготовка к олимпиадам, научно-творческим конференциям, проведение в школе "дней математики", сочинение математических игр, сказок и др. На уроках – это самостоятельные работы, требующие умения решать исследовательские задачи. V. Большой интерес вызывают у учащихся творческие самостоятельные работы, которые предполагают высокий уровень самостоятельности. Это задания на поиск второго, третьего и т. д. способа решения задач. Например, для нахождения высоты, опущенной из вершины прямого угла, если известны три элемента данного треугольника, можно применить способы, основанные на следующих фактах: на определении синуса острого угла, на вычисление формулы площади треугольника, на теореме Пифагора. VII. Контрольные работы являются необходимым условием достижения планируемых результатов обучения. По существу разработка текстов контрольных работ должна быть одной из основных форм фиксирования целей обучения, в том числе и минимальных. Поэтому во – первых, контрольные задания должны быть равноценными по содержанию и объему работы; во – вторых они должны быть направлены на отработку основных навыков; в – третьих, – обеспечить достоверную проверку уровня обучения: в – четвертых, они должны стимулировать учащихся, позволять их продемонстрировать прогресс в своей общей подготовке К самостоятельным работам можно отнести и тестовые задания. Актуальность введения тестирования в школьную практику обусловлена тем, что все чаще ученикам предлагают именно такие формы проверочных заданий на уровне города, округа и в ВУЗах. Основными достоинствами тестовой формы контроля знаний является: учет индивидуальных способностей учащихся; контроль качества усвоения не только практического, но и теоретического учебного материала; возможность детальной проверки усвоения учащимися каждой темы курса; осуществление оперативной диагностики уровня усвоения учебного материала – каждым учеником; экономия учебного времени при контроле знаний и оценки результатов обученности; разнообразие форм контроля. На уроках учитель сталкивается с самой трудной и почти неразрешимой проблемой – нехваткой времени. Ведь хочется в один час урока, порой, включить и устный счет, и тренировочные упражнения, и проверочную работу, и …. При этом, конечно же, на рассказы об ученых практически не остается времени. На своих уроках я пытаюсь совместить “приятное” с “полезным”, предлагая учащимся для выполнения и проверки своих знаний серию тестовых заданий по различным темам курса математики. “Изюминка” в том, что эти работы сопровождаю маленькой информацией о том или ином математике. Тема: «Исследование функции с помощью производной». Алгебра, 10 кл. Уровень А. Задание. Перед Вами – график некоторой функции. Исследуя данный график, постарайтесь ответить на поставленные вопросы о свойствах функции. Ниже дана таблица ответов. Впишите в строку "Буква" этой таблицы букву выбранного Вами правильного варианта. Из полученных букв составьте имя известного математика, который внес большой вклад в развитие алгебры. Прочитайте краткую информацию об этом ученом. 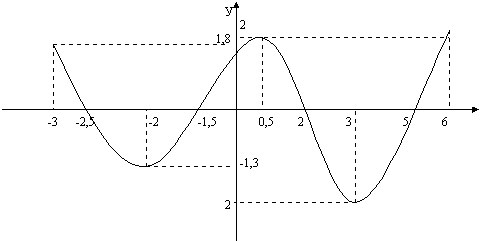
Таблица ответов:
………(1845-1918) - немецкий математик, творец теории множеств; дал обоснование теории действительных чисел. Его идеи и работы оказали большое влияние на развитие математики в целом, на понимание ее основ. Он получил ряд замечательных результатов, относящихся к теории бесконечных множеств, теории действительного числа. Ответ: Георг Кантор. Следует помнить, что тестовую форму контроля знаний следует использовать только в сочетании с традиционными контрольными и самостоятельными работами. Таким образом, образовательные стандарты и способы оценки их достижения являются ключевыми моментами, определяющими качество образования. Качество образования в значительной степени зависит от методической системы личности – ориентированного обучения, от умения учителя использовать ее таким образом, чтобы она способствовала активизации мыслительной деятельности учащихся, развивала их творческий потенциал, повышала самостоятельность учащихся. Образовательный процесс личностно – ориентированного обучения предоставляет каждому ученику, опираясь на его способности, склонности, интересы, ценностные ориентации и субъективный опыт, возможность реализовать себя в познании, учебной деятельности поведения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||