Методические рекомендации по выполнению контрольной работы по дисциплине «Прикладная математика»
 Скачать 365.62 Kb.
|
Таблица выбора вариантов
3.3. Задания для контрольной работы 3.3.1.Производная функции одной переменной Найти производные функций одной переменной; 1.  ; 2.  ; 3.  4.  ; 5.  ;6.  ;7.  ; 8.  ; 9.  ; 10.  . 3.3.2. Приложение производной и дифференциала к решению задач. 11.а) Точка движется по закону  . Найти величину скорости и ускорения в момент t=3 с, если путь измеряется в метрах.б) Сторона квадрата равна 10 дм. Найти приближенное приращение его площади при увеличении стороны на 0,1 дм. 12.а) Тело вращается вокруг оси по закону  . Найти угловую скорость вращения в момент t=1 c; угловое ускорение в момент t.б) Шар радиуса R=20 см был нагрет, в результате чего его объем увеличился на 40,5 см3. Вычислить приближенно удлинение радиуса шара. 13.а) Определить скорость движения точки в конце третьей секунды, если путь, пройденный точкой в t секунд, выражается формулой  и измеряется в метрах.б) Сторона куба, равная 0,7 м, удлинилась на 5 см. На сколько при этом приближенно увеличится объем куба? 14.а) Температура тела Т изменяется в зависимости от времени t по закону  . С какой скоростью нагревается это тело в момент t=4 c?б) Шар радиуса R=15 дм был нагрет, в результате чего длина радиуса увеличилась на 1 см. Найти приближенное значение приращения объема шара. 15.а) Количество электричества, протекшее через проводник за t секунд, определяется по формуле  . Найти силу тока в конце четвертой секунды.б) В прямоугольном параллелепипеде с квадратным основанием сторона основания равна 40 дм, а высота равна 20 дм. На сколько приближенно увеличится его объем, если сторону основания удлинить на 0,2 см? 16.а) Тело движется по закону  . Найти, в какие моменты времени скорости движения тела равны нулю?б) Радиус основания конуса равен 20 дм, а высота равна 25 дм. На сколько приближенно увеличится его объем, если радиус основания увеличить на 0,05 дм? 17.а) Угол поворота шкива определяется из уравнения  , где t время в секундах. Найти среднюю угловую скорость в промежутке времени от t=4 до t=6 и угловую скорость в момент t=6.б) Куб со стороной а=20 см был нагрет, в результате чего сторона его увеличилась на 0,01 см. найти приближенное значение приращения объема куба. 18.а) Тело вращается вокруг оси, причем закон изменения угла в зависимости от времени t определяется уравнением  . Найти угловую скорость вращения тела в момент t=3.б) Сторону куба, равную 0,6 м, удлинили на 1 см. На сколько при этом приближенно увеличится объем куба? 19.а) Тело движется по закону  . Найти максимальную скорость движения тела.б) в конусе радиус основания равен 25 дм, а высота его равна 2 дм. На сколько приближенно увеличится его объем, если радиус основания удлинить на 0,1 см? 20.а) Тело, брошенное вертикально вверх со скоростью v0 м/с, движется по закону  , где время t – в секундах, а путь s – в метрах. Найти скорость движения и ускорение в момент t; в конце третьей секунды, если v0=100 м/с.б) Шар радиуса R=20 дм был нагрет, в результате чего длина радиуса увеличилась на 0,3 см. Найти приближенное значение приращения объема шара. 3.3.3.Приложение производной и дифференциала к исследованию и построения графика функции. Исследовать функцию и построить ее график.      ,   ,  3.3.4 Интегральное исчисление а) Найти интегралы. б) Найти площадь плоской фигуры, ограниченной указанными линиями. Выполнить схематический чертеж. в) Найти объём тела вращения плоской фигуры, ограниченной указанными линиями. Выполнить схематический чертеж. 31. а)  ; б) y=x2-4x+3, осями координат и прямыми x=-1, x=3; в) Эллипс - вокруг малой оси: 4x2+9y2=36 32. а)  ;б) y=3/x, x+y-4=0; в) Эллипс - вокруг большой оси: 4x2+9y2=36. 33. а)  ; б) y=3x-x2, 5x-y-8=0; в) Дуга окружности x2+y2=16 в первой четверти между прямыми x=1 и x=3. 34. а)  ;б) y2=16x, y=x; в) Y2=4x, y=x, вокруг оси ох. 35. а)  б) между параболами y=8x-x2 и y=x2+18x-12; в) Y=x2, y2=8x, вокруг оси ох. 36. а)  ;б) между y=x2/2 и y=  ;в) Y=x2, y2=8x, вокруг оси оу. 37. а)  ; б) Y2=2x и x2+y2=8, осью ох; в) Y2=4ax, x=0, x=8, вокруг оси ох 38. а)  ; б) X2+y2=25, 2y-5=0; в) Y2=3x, x=1, x=3, вокруг оси ох 39. а)  ;б) x2+y2=16, x+y-4=0; в) Одной полуволны y=cos x, вокруг оси ох 40. а)  ;б) y=2-x2, y=x. в) Y2=3+x, x=3, вокруг оси ох. 3.3.5 Элементы линейной алгебры Решить систему методом Крамера и матричным способом: 41 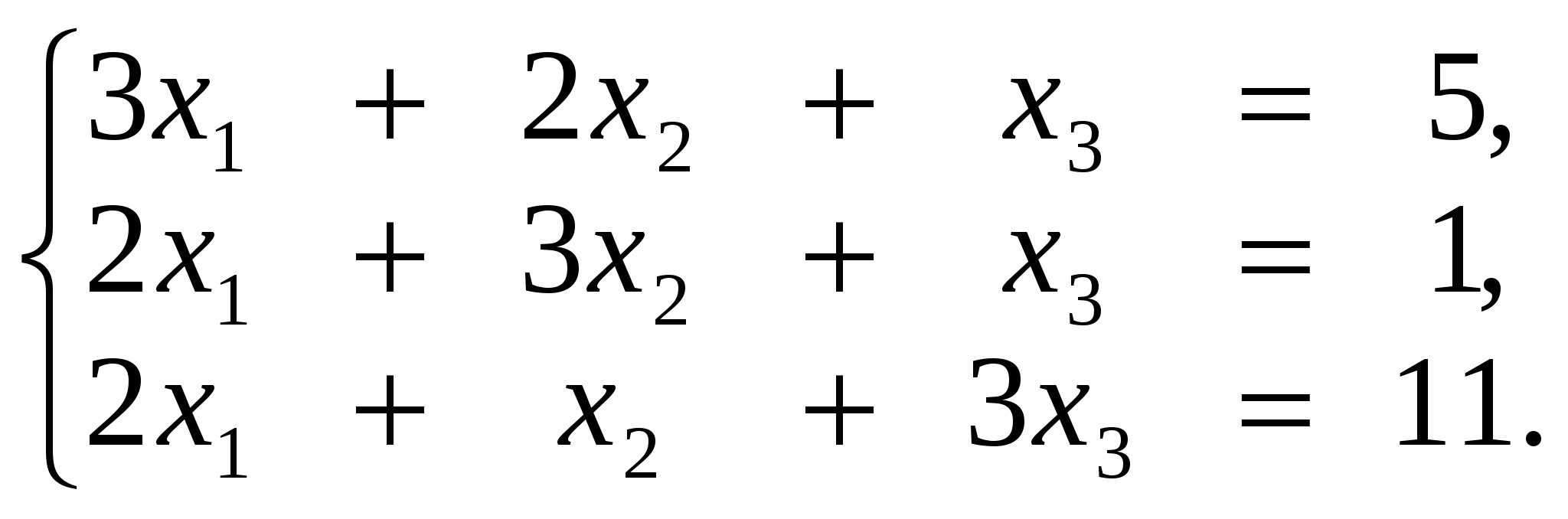 42  43 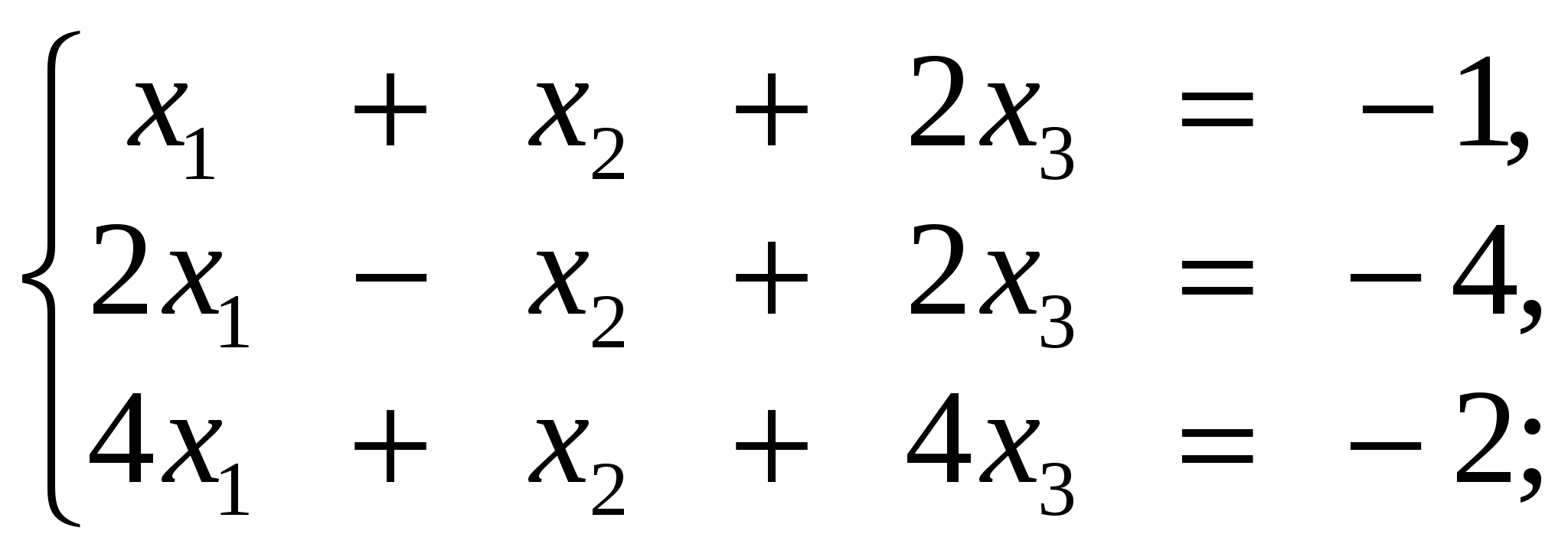 44 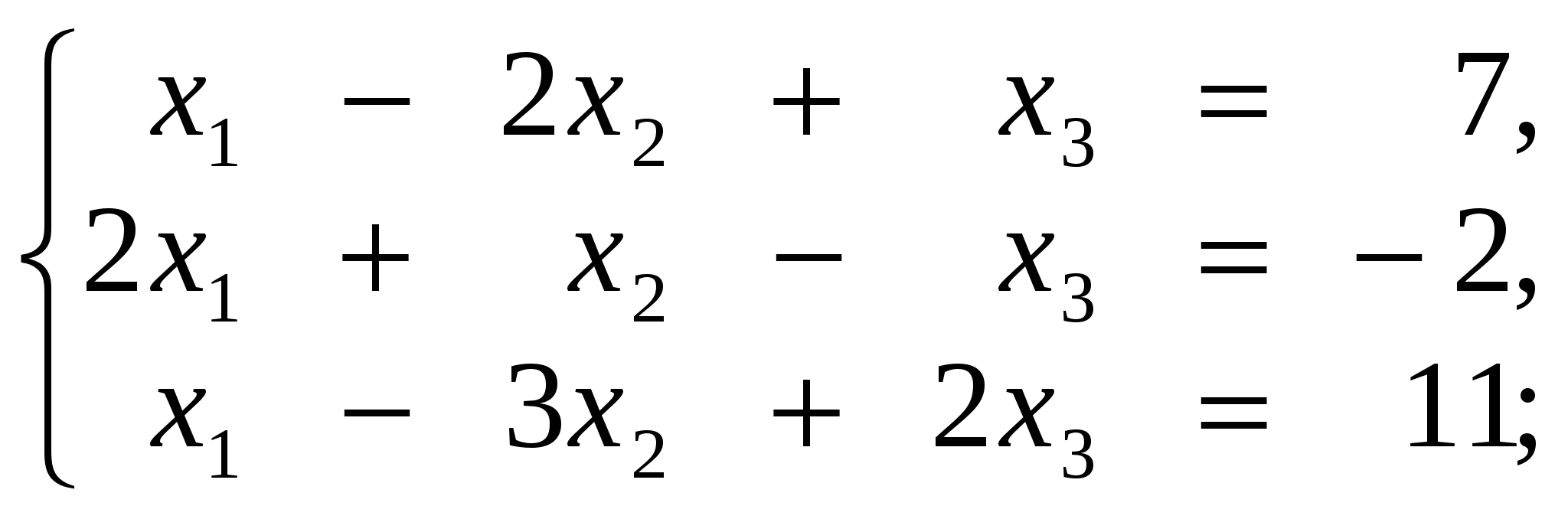 45 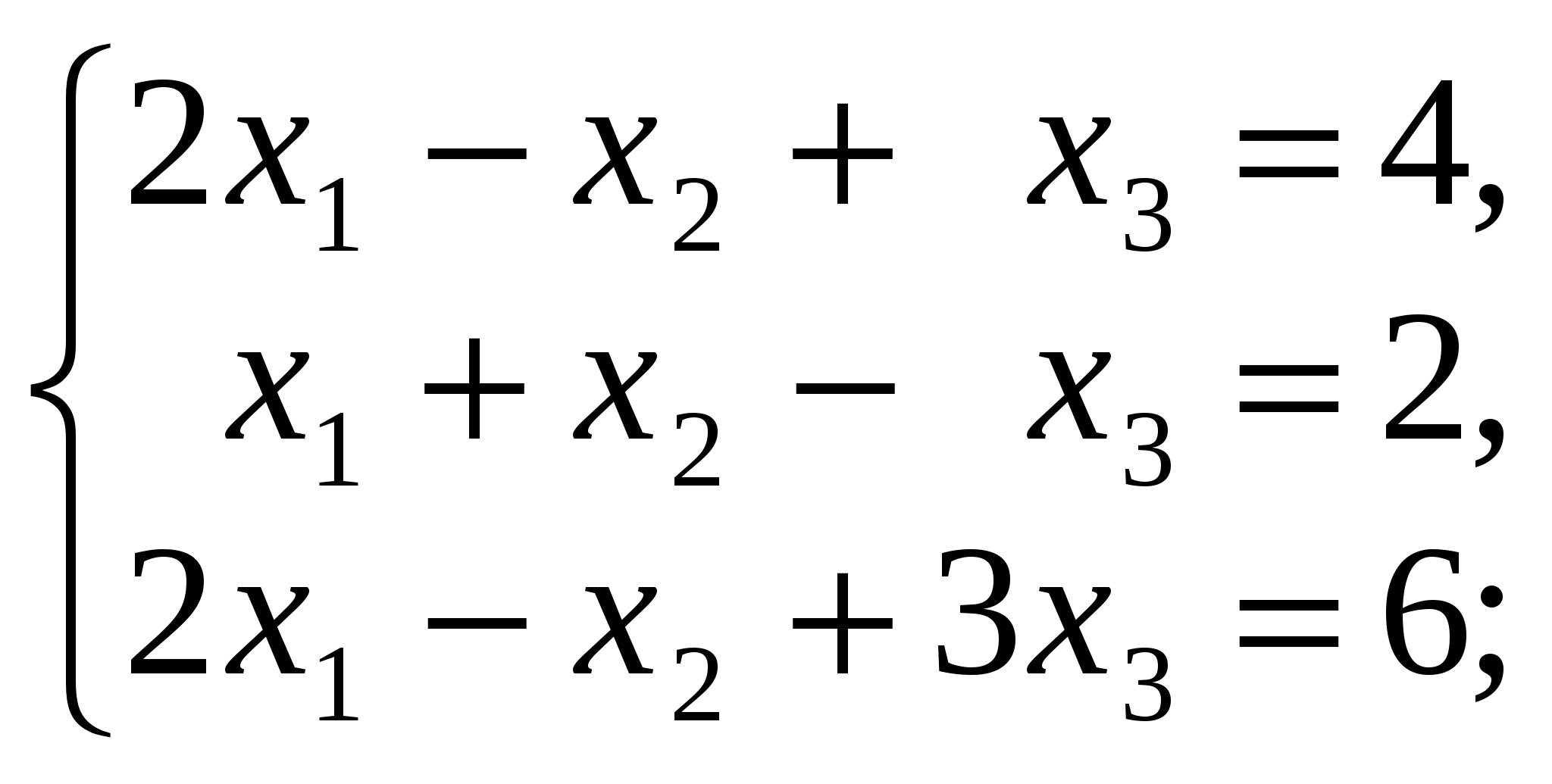 46 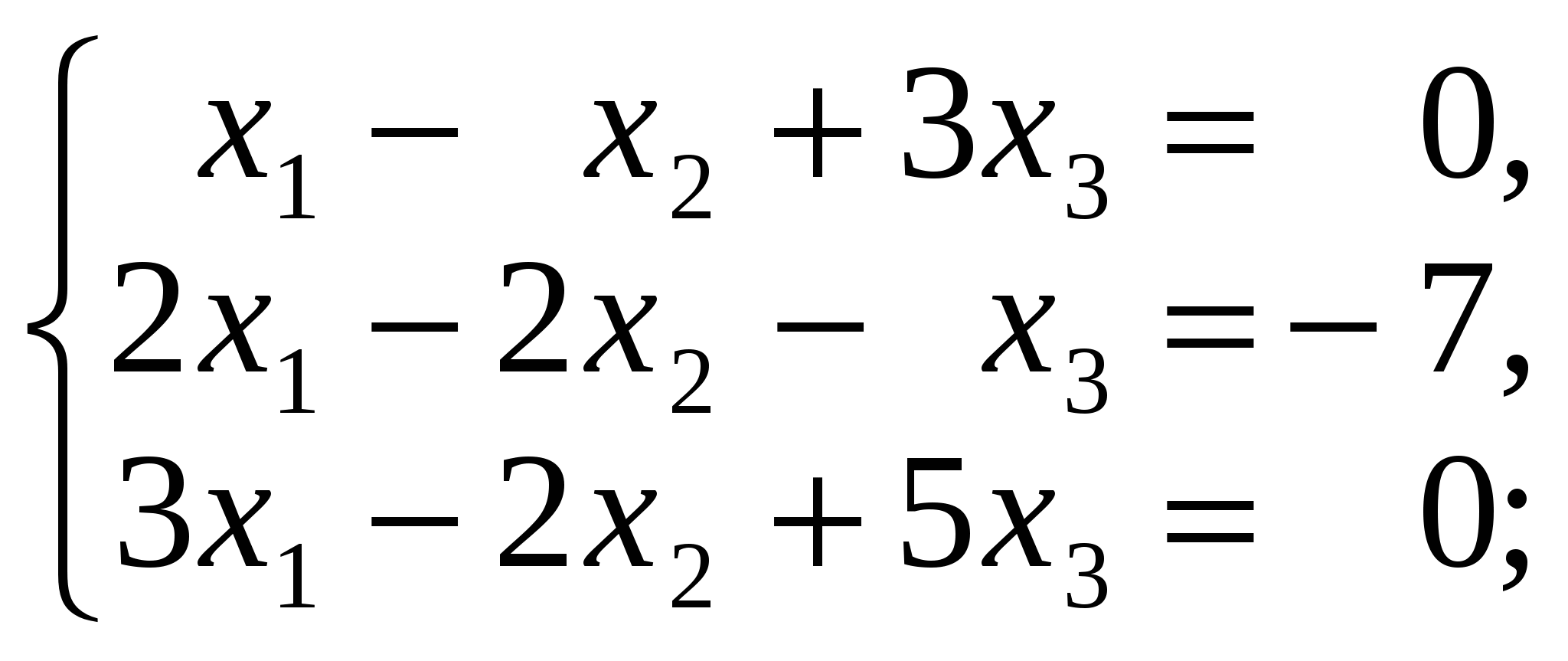 47 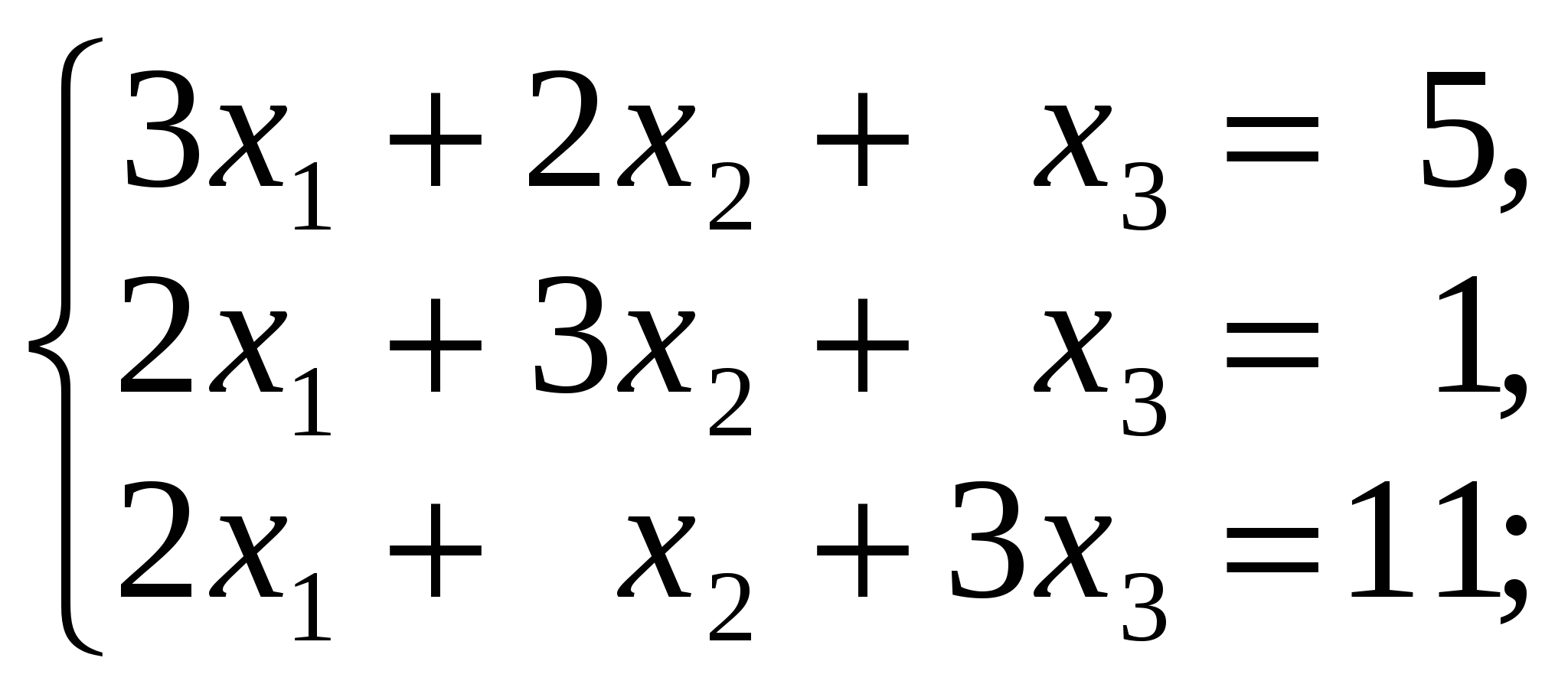 48 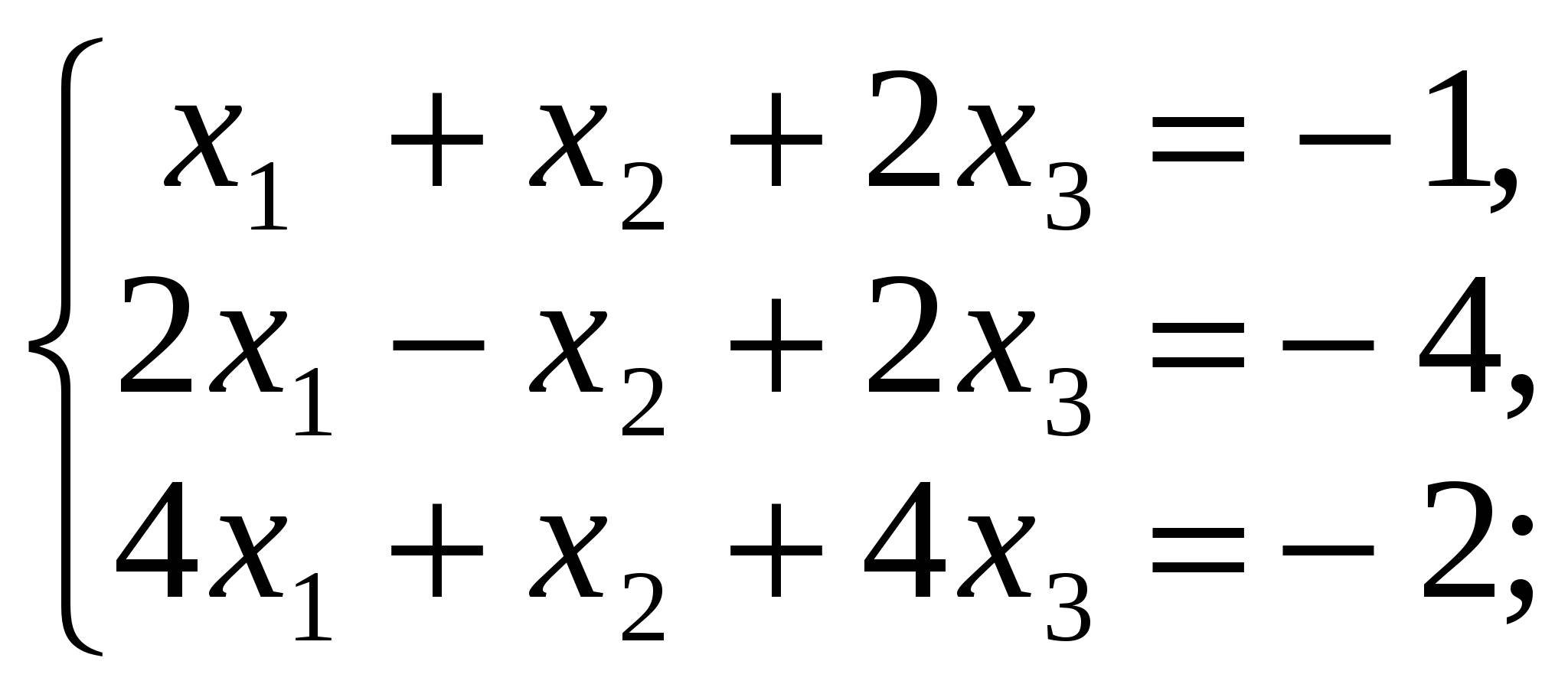 49 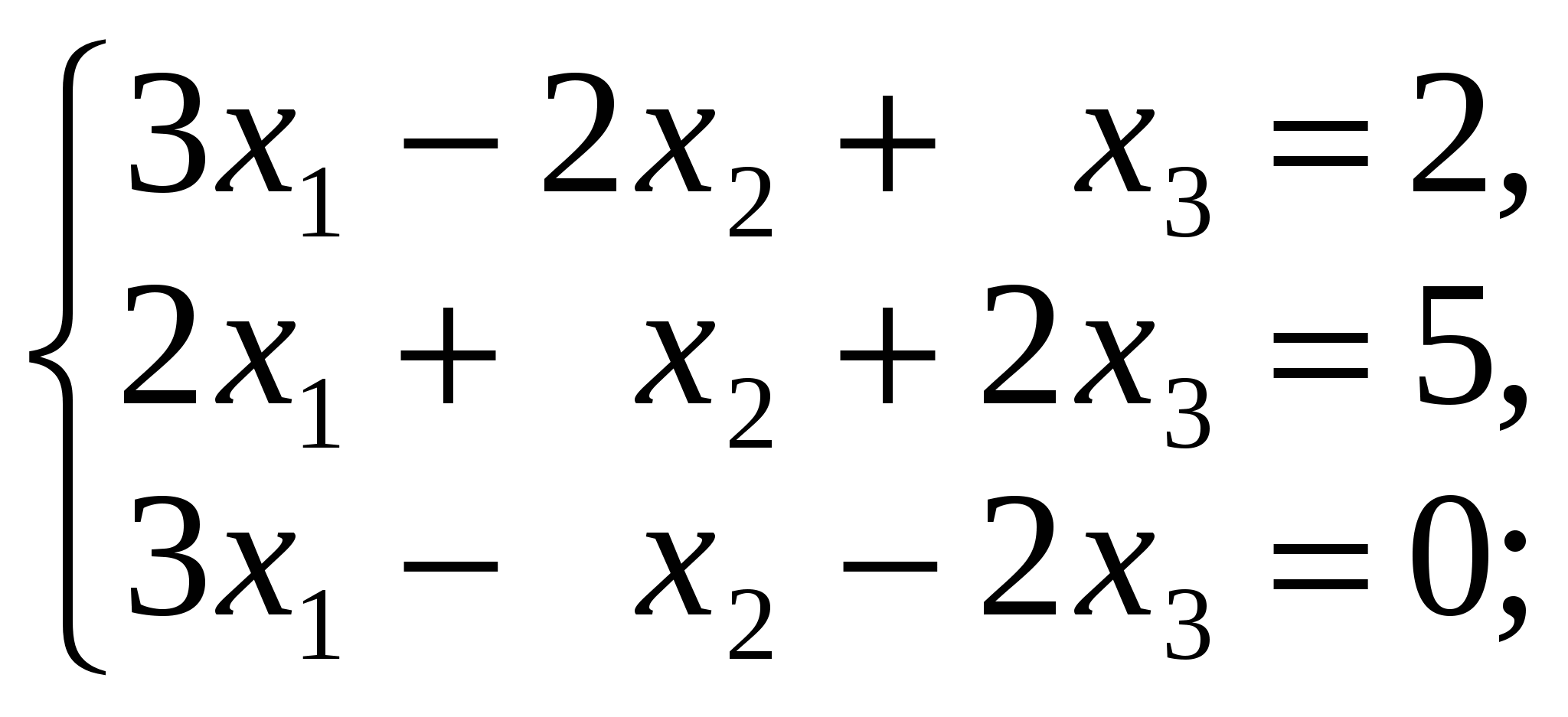 50 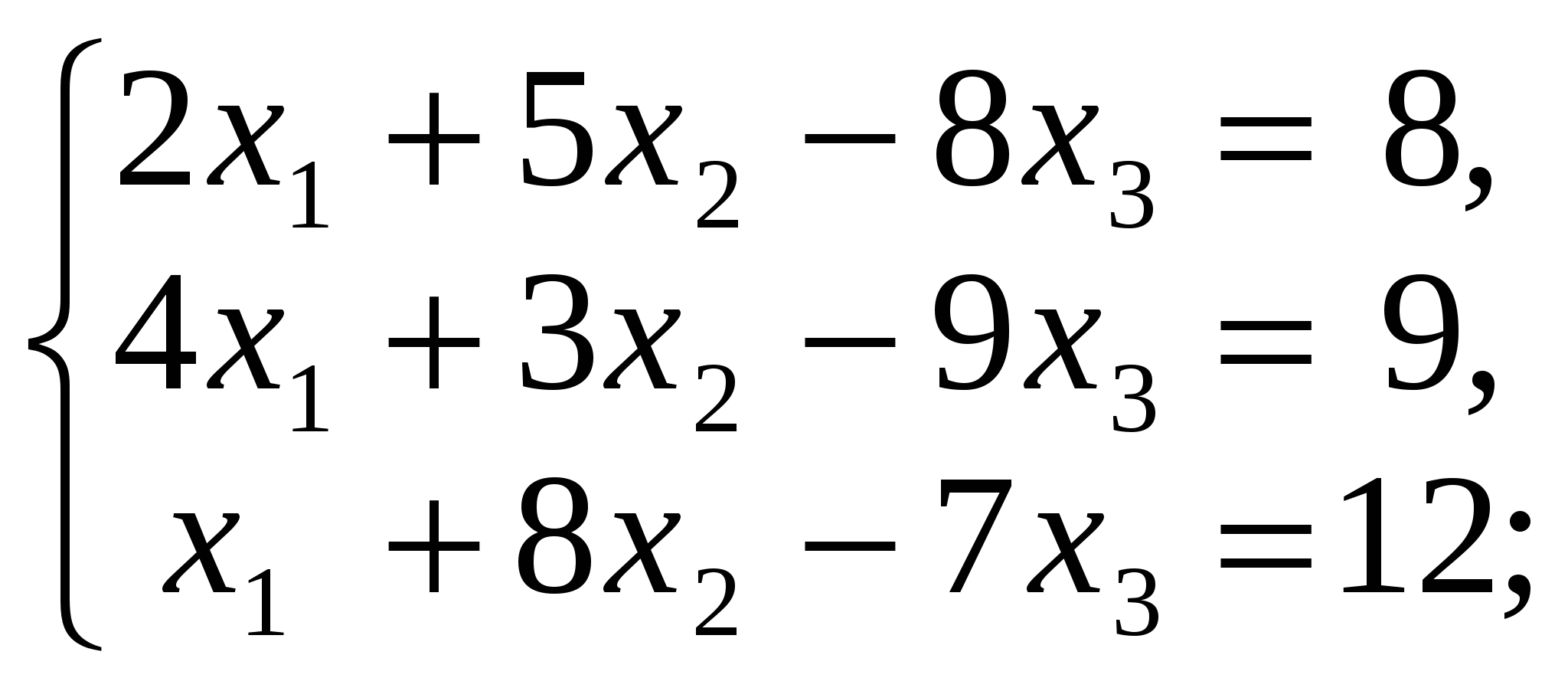 3.3.6.Теория комплексных чисел Выполнить действия в алгебраической форме и представить полученный результат в тригонометрической и в показательной форме. 71. а)  ;72. а)  ;73. а)  ; 74. а)  ; 75. а)  ; 76. а)  ; 77. а)  ; 78. а)  ;79. а)  ; 80. а)  .3.3.7. Элементы комбинаторики и теории вероятностей 81. а) Сколькими способами из группы, включающей 25 учащихся, можно выбрать актив группы в составе старосты и профорга? б) В урне находится 7 красных и 6 синих шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара красные. 82. а) Найти количество всех трехзначных чисел, состоящих из чисел 1,2,3,4,5. б) Набирая номер телефона, абонент забыл три последние цифры, и помня только, что они различны, набрал их наудачу. Какова вероятность, что он набрал нужные цифры. 83. а) Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек. б) К концу дня в магазине осталось 60 арбузов, из которых 50 спелых Покупатель выбирает 2 арбуза. Какова вероятность, что оба арбуза спелые? 84. а) Сколько всего игр должны провести 20 футбольных команд в однокруговом чемпионате? б) Девять книг, из которых 4 одинаковые, а остальные различны, расставлены наудачу на одной полке. Найти вероятность того, что эти 4 книги окажутся поставленными рядом. 85. а) В третьем классе изучается 10 предметов. В понедельник 4 урока. Сколькими способами можно составить расписание на этот день б) В партии из 24 деталей 6 бракованных. Из партии выбирают наугад детали. Найти вероятность того, что они все будут бракованными. 86. а) Сколькими способами можно из 20 человек назначить двух дежурных, из которых один старший? б) Карточка «Спортлото» содержит 49 чисел. В тираже участвуют 6 чисел. Какова вероятность того, что будет верно угадано 4 числа? 87. а) В подразделении 30 солдат и 3 офицера. Сколькими способами можно выделить патруль, состоящий из 3 солдат и одного офицера? б) Из группы, состоящей из 10 юношей и 8 девушек, выбирают по жребию дежурных. Какова вероятность того, что все выбранные окажутся юношами? 88. а) Из 8 различных цветков нужно составить букет так, чтобы в него входило не менее 2 цветков. Сколько существует способов для составления такого букета? б) Студент знает 20 из 25 вопросов программы. Вычислить вероятность того, что студент знает 2 вопроса из билета. 89. а) Сколькими способами можно выбрать четырёх человек на четыре различные должности из девяти кандидатов на эти должности? б) В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что 4 наугад выбранных билета будут выигрышными? 90. а) Из 7 бегунов и 3 прыгунов нужно составить команду из 5 человек, в которую должен входить хотя бы один прыгун. Сколькими способами это можно сделать?) В партии из 10 деталей имеются 3 нестандартных. Найти вероятность того, что 3 наудачу взятые детали
Раздел 1. Математический анализ Определение производной. Производной функции f(x) в точке х0 называется предел отношения приращения  функции в этой точке к приращению  аргумента, когда последнее стремиться к нулю: .Для производной функции у = f(x) употребляются обозначения:  или  .Функция f(x) , имеющая производную в каждой некоторого промежутка , называется дифференцируемой в этом промежутке. Производная сложной функции. Теорема: Если функция x=  имеет производную в точке t0, а функция f(x) имеет производную в точке x0= , то сложная функция  имеет производную в точке t0, определяемую по формуле  Пример: Найти производную функции y= ln5sinx. Сначала дифференцируем степенную функцию, затем -логарифмическую, затем- тригонометрическую. Полученные производные перемножаем.  Пример исследования функции. 1). Найти область определения функции. 2). Проверить функцию на четность или нечетность, периодичность. 3). Найти асимптоты графика функции, 4). Найти точки пересечения график функции с осями координат. 5). С помощью первой производной найти промежутки монотонности, ее экстремумы. 6). С помощью второй производной найти промежутки выпуклости и вогнутости, точки перегиба. 7). По результатам исследования построить график функции. Пример: Исследовать и построить график функции 
Точка x=1- точка разрыва второго рода, так как  то x=1-вертикальная асимптота.Горизонтальной асимптоты нет, так как  Наклонная асимптота: найдем k и b.  Тогда, уравнение наклонной асимптоты y= x+1.
Занесем результаты в таблицу
С 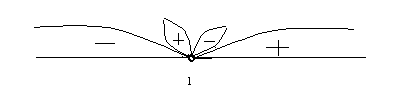 оставим таблицу:
 х Практика показывает, что часто приходится по заданной производной или по заданному дифференциалу функции находить функцию, от которой была взята производная и дифференциал, т.е. выполнять обратную задачу дифференцированию – интегрирование. Функция F(x) называется первообразной для функции f(x) на интервале (a;b), если в любой точке этого промежутка ее производная равна f(x), т.е. F(x)=f(x), х(a;b) Совокупность первообразных для функции f(x) или для дифференциала f(x)dx называется неопределенным интегралом и обозначается символом  , гдеf(x) – подынтегральная функция f(x)dx – подынтегральное выражение c – произвольная постоянная. Основные свойства неопределенного интеграла: 1. Производная неопределенного интеграла равна подынтегральной функции, т.е.  2. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла, т.е.  , где m=const3. Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от этих функций, т.е.  .4. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.  5. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С, т.е.  или  Если F(x)+C- первообразная функция для f(x), то приращение F(b)-F(a) первообразных функций при изменении аргумента x от x=a до x=b называется определенным интегралом и обозначается символом  , т.е.  , гдеa – нижний предел определенного интеграла b – верхний предел определенного интеграла. Основные свойства определенного интеграла: 1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:  .2. Постоянный множитель можно вынести за знак определенного интеграла, т.е.  , где m=const3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов от этих функций, т. е.  4. Если a, b, c принадлежат интервалу, на котором функция непрерывна, то  Определенный интеграл широко применяется на практике, в частности, при вычислении площадей плоских фигур и объемов тел вращении Раздел 4. Линейная алгебра Определители второго и третьего порядков. |
, но x=1-не принадлежит области определения функции. Решим неравенства методом интервалов. Отметим знаки интервалов на числовой прямой, учитывая кратность x=1.
(-0,4;1)
(x)
Критические точки: x=1, но она не принадлежит области определения функции. Решим неравенства методом интервалов : (x-1)3<(>)0.
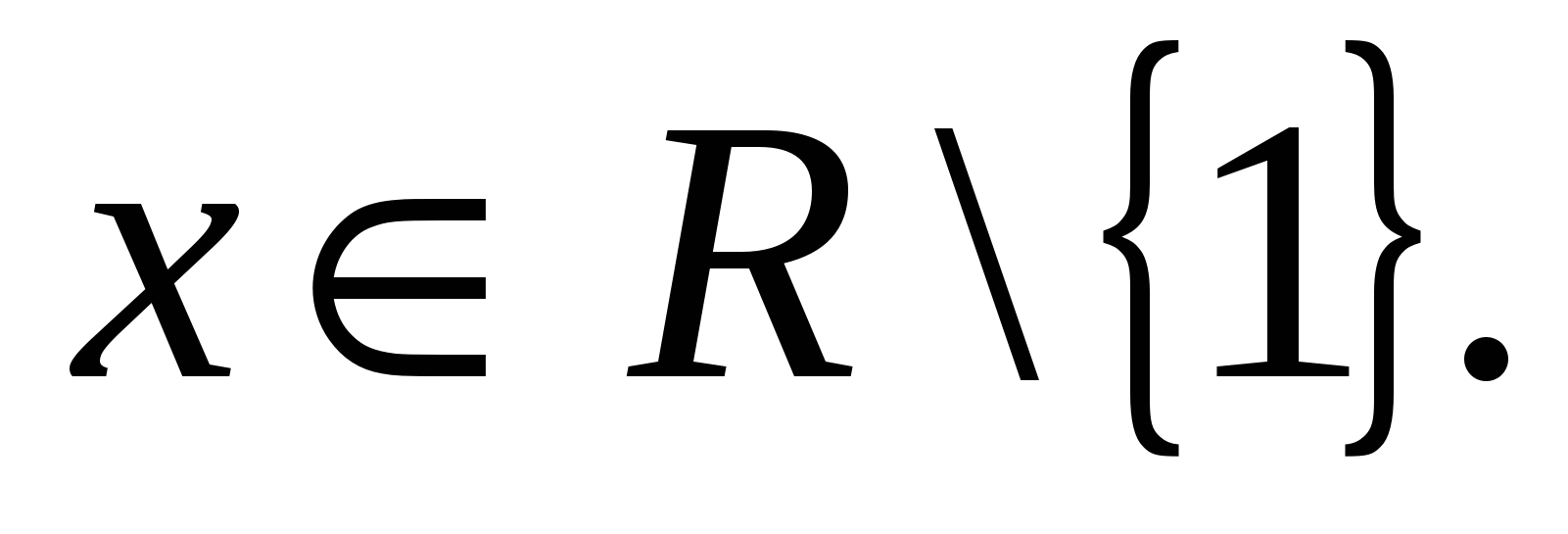
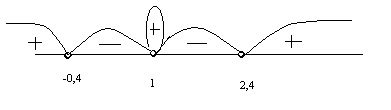
(x)
