Решение. Рассмотрим события a = «учащийся решит 11 задач» иВ = «учащийся решит больше 11 задач»
 Скачать 178.65 Kb.
|
| ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТИ С РЕШЕНИЯМИ
Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07. Ответ: 0,07.
Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156. Ответ: 0,156.
Решение. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035. Ответ: 0,035.
Решение. Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов. Пусть A, B, C и D — это события, в которых З. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 70 баллов. Тогда поскольку  для вероятности поступления имеем:   Ответ: 0,408.
Решение. Пусть завод произвел  тарелок. В продажу поступят все качественные тарелки и 20% невыявленных дефектных тарелок:  тарелок. Поскольку качественных из них  , вероятность купить качественную тарелку равна 
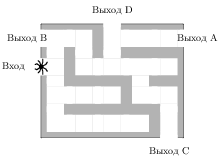 Решение. 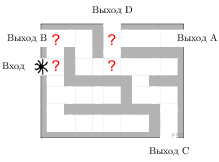 На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625. Ответ: 0,0625
Решение. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975. Ответ: 0,9975. Приведем другое решение. Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем: P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975.
Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09. Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91. Ответ: 0,91.
Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», тогда A + B = «чайник прослужит больше года». События A и В совместные, вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Вероятность произведения этих событий, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда: P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B), откуда, используя данные из условия, получаем 0,97 = P(A) + 0,89. Тем самым, для искомой вероятности имеем: P(A) = 0,97 − 0,89 = 0,08. Ответ: 0,08.
Решение. Пусть событие  состоит в том, что яйцо имеет высшую категорию, события  и  состоят в том, что яйцо произведено в первом и втором хозяйствах соответственно. Тогда события  и  — события, состоящие в том, что яйцо высшей категории произведено в первом и втором хозяйстве соответственно. По формуле полной вероятности, вероятность того, что будет куплено яйцо высшей категории, равна:   Поскольку по условию эта вероятность равна 0,35, поэтому для вероятности того, что купленное яйцо произведено в первом хозяйстве имеем:  Примечание Ивана Высоцкого. Это решение можно записать коротко. Пусть  — искомая вероятность того, что куплено яйцо, произведенное в первом хозяйстве. Тогда  — вероятность того, что куплено яйцо, произведенное во втором хозяйстве. По формуле полной вероятности имеем:  Ответ: 0,75. Приведем другое решение. Пусть в первом хозяйстве агрофирма закупает яиц, в том числе,  яиц высшей категории, а во втором хозяйстве —  яиц, в том числе  яиц высшей категории. Тем самым, всего агроформа закупает  яиц, в том числе  яиц высшей категории. По условию, высшую категорию имеют 35% яиц, тогда: Следовательно, у первого хозяйства закупают в три раза больше яиц, чем у второго. Поэтому вероятность того, что купленное яйцо окажется из первого хозяйства равна 
Решение. Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52. Ответ: 0,52. Приведем другое решение. Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52.
Решение. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35. Ответ: 0,35.
Решение. Рассмотрим события А = кофе закончится в первом автомате, В = кофе закончится во втором автомате. Тогда A·B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате. По условию P(A) = P(B) = 0,3; P(A·B) = 0,12. События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения: P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52. Ответ: 0,52. Приведем другое решение. Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятость х = 0,52. Примечание. Заметим, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.
Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна  Ответ: 0,02.
Решение. Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем:    Ответ: 0,0545.
Решение. Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836. Ответ: 0,8836.
Решение. Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем:  Ответ: 0,0296.
Решение. Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135. Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055. Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019. Ответ: 0,019.
Решение. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна  Ответ: 0,027.
Решение. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна Ответ: 0,027.
Решение. Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38. Ответ: 0,38.
Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
Решение. Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды: P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128; P(OXO) = 0,2·0,2·0,2 = 0,008; P(OOO) = 0,2·0,8·0,8 = 0,128. Указанные события несовместные, вероятность их сумы равна сумме вероятностей этих событий: P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392. Ответ: 0,392.
Решение. Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия): ...Д...Ш...Н..., ...Д...Н...Ш..., ...Ш...Н...Д..., ...Ш...Д...Н..., ...Н...Д...Ш..., ...Н...Ш...Д... Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна  Ответ: 0,33. Замечание. Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из  предыдущих групп: оно равно  Общее количество перестановок из всех групп равно  Поэтому искомая вероятность равна 
Решение. Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за n выстрелов. Вероятность промахнуться при первом выстреле равна 0,6, а при каждом следующем — 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при n выстрелах равна:  Осталось найти наименьшее натуральное решение неравенства  Последовательно проверяя значения , равные 1, 2, 3 и т. д. находим, что искомым решением является  . Следовательно, необходимо сделать 5 выстрелов. Ответ: 5. Примечание. Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов: Р(1) = 0,6. Р(2) = Р(1)·0,4 = 0,24. Р(3) = Р(2)·0,4 = 0,096. Р(4) = Р(3)·0,4 = 0,0384; Р(5) = Р(4)·0,4 = 0,015536. Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени. Приведем другое решение. Вероятность поразить мишень равна сумме вероятностей поразить ее при первом, втором, третьем и т. д. выстрелах. Поэтому задача сводится к нахождению наименьшего натурального решения неравенства  В нашем случае неравенство решается подбором, в общем случае понадобится формула суммы геометрической прогрессии, использование которой сведет задачу к простейшему логарифмическому неравенству.
Решение. Команда может получить не меньше 4 очков в двух играх тремя способами: 3+1, 1+3, 3+3. Эти события несовместны, вероятность их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем:   Ответ: 0,32.
Решение. Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна  . Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна  . Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна  Ответ: 0,1. Приведем комбинаторное решение. Всего способов выбрать 3 учащихся из 21 учащегося класса равно  . Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно  способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно  способами. Поэтому вероятность того, что девочки окажутся в одной группе равна  Приведем еще одно решение. Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Решение. Двухрублевые монеты могут лежать в одном кармане, если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:  Ответ: 0,4. Приведем другое решение. Количество способов взять 3 монеты из 6, чтобы переложить их в другой карман, равно  Количество способов выбрать 3 рублевых монеты из 4 рублевых монет равно 4. Количество способов взять вместе с двумя двухрублевыми монетами одну рублевую монету из имеющихся 4 рублевых монет тоже равно 4. Поэтому искомая вероятность того, что двухрублевые монеты лежат в разных карманах, равна
Решение. Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:  Другое рассуждение. Вероятность того, что Петя взял пятирублевую монету, затем десятирублевую, и затем еще одну десятирублевую (в указанном порядке) равна  Поскольку Петя мог достать пятирублевую монету не только первой, но и второй или третьей, вероятность достать набор из одной пятирублевой и двух десятирублевых монет в 3 раза больше. Тем самым, она равна 0,6. Ответ: 0,6. Приведем другое решение. Количество способов взять 3 монеты из 6, чтобы переложить их в другой карман, равно Количество способов выбрать 1 пятирублевую монету из 2 пятирублевых монет и взять вместе с ней еще 2 десятирублевых монеты из имеющихся 4 десятирублевых монет по правилу произведения равно  Поэтому искомая вероятность того, что пятирублевые монеты лежат в разных карманах, равна 
Решение. Возможны три варианта: орел-орел-решка, орел-решка-орел, решка-орел-орел. Эти события несовместные, вероятность их суммы равна сумме вероятностей этих событий:  Приведем другое решение. Можно перечислить все возможные случаи бросания монетки (О — орел, Р — решка): ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР и найти, в скольких из них орел выпал ровно два раза: ООР, ОРО, РОО. Тем самым, вероятность выпадения орла дважды равна 3 : 8 = 0,375. (Этот подход затруднителен в случае большого числа бросаний монетки.) Приведем еще одно решение. Вероятность выпадения монетки одной стороной и дважды — другой стороной равна 0,5·0,5·0,5 = 0,125. Выбрать из этих «трех» сторон два орла можно  способами. Следовательно, искомая вероятность равна 0,375. Примечание. Последнее рассуждение — не что иное, как вывод формулы Бернулли для нашего случая. В общем случае, если проводится испытаний, в каждом из которых некоторое событие наступает в вероятностью  , то вероятность наступления этого события ровно  раз дается формулой  Источник информации: Решу ЕГЭ. Образовательный портал для подготовки к экзаменам. Математика. Режим доступа: https://reshuege.ru/test?theme=185 |
.