«Проектная деятельность на уроках математики». ( выступление на шмо учителей математики). Учитель математики мбоу сош №6
 Скачать 57.57 Kb. Скачать 57.57 Kb.
|
| «Проектная деятельность на уроках математики». ( выступление на ШМО учителей математики). Учитель математики МБОУ СОШ № 6 Калашникова Любовь Михайловна Январь 2012 года Очень хорошо помогать своим ученикам и направлять их на верный путь. Но все это нужно делать очень осторожно, нужно делать это так, чтобы ученик не заметил помощи и подсказки и верил, что все это он делает сам. (Ф. Нейман ) С каждым годом школьное образование все больше реформируется и изменяется, поэтому в обучении появляются новые формы, методы и приемы. Однако и современные учителя используют способы обучения. Разработанные много лет назад. Метод проектов возник в 20-е годы прошлого столетия в США. Его также называли методом проблем. Основоположники этого метода – американский философ и педагог Дж. Дьюи , а также его ученик У.Х. Килпатрик. Идея этого метода : вовлечь каждого ученика в активный познавательный творческий процесс. У Килпатрик выделил несколько типов проекта: потребительский: имеющий своей целью потребление в широком значении слова, включая развлечение), проблемный ( представляет проект решения каких либо интеллектуальных препятствий, выступающих сопутствующими в создающемся проекте) и проект – упражнение. Дж.Дьюи предлагал строить обучение на активной основе, через целесообразную деятельность ученика, сообразуясь с его личным интересом именно в этом знании. У.Х. Килпатрик продолжил дело своего учителя. Главная его идея в методе проектов составляет следующие: деятельность ребенка должна выполняться с большим увлечением, которую выбрал он сам свободно, и она не должна строиться в русле учебного предмета. Лозунгом всей этой деятельности были слова: « Всё из жизни – всё для жизни». В современном понимании проектная деятельность- это способ достижения дидактической цели через детальную разработку проблемы, которая должна завершиться вполне реальным практическим результатом, оформленным тем или иным образом. Цели проектной деятельности таковы: воспитание людей, способных быть самостоятельными в мышлении и действиях; Развитие коммуникативных исследовательских навыков, умение работать с информацией, формулировать проблемы и находить пути их решения; развитие у учащихся критического мышления. Основные требования к использованию метода проектов:
Эти требования должны пронизывать все стадии осуществления проектной деятельности:
Метод проектов можно использовать в учебном процессе для решения различных небольших проблемных задач в рамках одного- двух уроков (мини проекты или краткосрочные проекты) В этом случае тема проекта связана с темой урока или применением данной темы в различных жизненных ситуациях. Примеры краткосрочных проектов ( в рамках изучения программного материала) 7 класс. Тема урока « Теорема о сумме углов треугольника». На каждой парте у учащихся произвольный треугольник. Как найти сумму углов этого треугольника? Это проблема и ее предлагается решить. Ученики работают в парах. Предлагают различные способы: а) измерение углов треугольника с помощью транспортира б) достроить треугольник до прямоугольника Роль учителя: направить поиск решения данной проблемы от экспериментального на путь доказательства и тут же поставить вопрос - а если сумма углов в треугольнике действительно меньше 180 градусов, а если больше 180 градусов? Т.е. учитель дает понять, что существуют и другие геометрии отличные от геометрии Евклида, где сумма углов меньше 180 градусов – геометрия Лобачевского, где сумма углов больше 180° - геометрия Римана. Эти геометрии выполняются в пространстве и имеют применение в жизни. Но мы находимся на плоскости и здесь выполняется геометрия Эвклида, где сумма углов в треугольнике равна 180 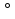 . Как это доказать? Организуется работа в группах по доказательству данной теоремы. . Как это доказать? Организуется работа в группах по доказательству данной теоремы.Результат решения проблемы три способа доказательства теоремы о сумме углов треугольника. 9 класс. Мини- проект был дан в форме домашнего задания к открытому уроку по теме « Квадратичная функция». Проект был представлен в виде презентации « Связь с реальным миром». Где учащиеся показали, что парабола встречается в жизни: траектория движения струи воды, попадание баскетбольного мяча в корзину, радуга, траектория движения комет, и так далее. 6 класс. Тема: « Координатная плоскость» Проблему предлагает учитель: - Вы все читали книгу Жюль Верна « Дети капитана Гранта». Вопрос, почему дети долго не могли найти своего отца? Как определить положение ладьи на шахматной доске? На экране вы видите билет. Какой билет? (ответ билет в цирк.) Что можно определить по этому билету? 10 класс. Тема : «Правильная пирамида.» После введения определения правильной пирамиды, ставлю проблему. Что общего для всех правильных пирамид? На столах учащихся разнообразные виды правильных пирамид: треугольная, четырехугольная, шестиугольная, восьмиугольная. Класс разбивается на 4 группы. Выдвигаются гипотезы, ведется исследование и от каждой группы выступление по поводу решения данной проблемы. Учитель должен продумывать весь ход работы на мини – проектом также , как и для решения более сложных для понимания вопросов. Ни саму проблему , ни гипотезы, ни методы исследования творческой, поисковой деятельности он не должен давать учащимся в готовом виде. Учитель лишь ненавязчиво направляет мысль учащихся в нужное русло. Но если ученики высказывают собственные суждения отличные от мнения учителя, более того, явно ошибочные с его точки зрения, учитель ни в коем случае не навязывает ребятам своего мнения. Для решения крупных задач ( проблем) по математике, сложных для пониманиях вопросов использую крупные проекты, которые в основном выполняются во внеурочной деятельности. Данные проекты в основном направлены на углубление и расширение знаний по математике. Этого так называемые среднесрочные проекты. ( макро- проекты), применяемые в основном во внеурочных формах работы ( кружки, факультативы, элективные курсы). Поле для выбора темы долгосрочных проектов по математике огромны. Проект может быть связан с изучением какой -либо темы по математике, которая не изучается в школьной программе или с приложениями математики в науке и практике. Примерами могут служить проекты последующим темам:
Для учащихся 11 класса разработала элективный курс по теме: « Решение уравнений высших степеней». Этот курс существенно дополняет школьный курс и необходим учащимся к подготовке в ЕГЭ. На вводном занятии знакомила учащихся с различными видами уравнений высших степеней. Сформулировали проблему: Найти способы решения данных уравнений. Используя литературу по теме, а также возможности интернета. Макро -проект разбили на мини- проекты для каждого учащегося. Например: формула Кардано, алгебраические уравнения и группы Галуа, схемы Горнера, и т.д. На итоговом занятии были заслушаны проекты выполненные учащимися. Оценивали каждый проект участники занятий, высказывая свое мнение по поводу каждого способа решения уравнений высших степеней. Результат элективного курса : учащиеся создали для себя методичку для решения уравнений высших степеней, в помощь для сдачи ЕГЭ. Рефлексия необходима после работы над любым проектом. Что вы приобрели для себя в процессе работы над проектом? Реализация методом проектов, методики сотрудничества перспективны при изучении математики; работа над проектами развивает мотивацию к обучению, более результативно, чем на традиционных уроках. Литература.
|