Решение логарифмических уравнений Цели урока
 Скачать 49.51 Kb.
|
| Разработка урока по алгебре и началам анализа в 11 классе по теме «Итоговое повторение. Решение логарифмических уравнений» Цели урока
- повторить основные алгоритмы решения логарифмических уравнений базового и повышенного уровня сложности путём вариативности заданий; - повторить основные формулы, связанные с логарифмами; - повторить решение некоторых других видов уравнений (показательно - логарифмичеких, с модулем, сумма квадрата и квадратного корня равна нулю и др.); - рассмотреть решение задания, содержащего параметр. 2. Развивающая: - развитие логического мышления учащихся; - развитие речевой и письменной культуры учащихся; - развитие умения применять имеющиеся знания в нестандартной ситуации. 3. Воспитательная: - умение работать в команде; -умение обоснованно отстаивать свою точку зрения; - воспитание уверенности в своих силах и знаниях; - развитие самостоятельности. Оборудование урока - карточки с индивидуальными заданиями для самостоятельной работы; - карточки с заданиями для домашней работы; - карточки с заданиями для групп; - документ – камера (или листы формата А1 и маркеры для каждой группы); - мультимедийный проектор, компьютер. Формы работы - фронтальная; - работа в группах; - индивидуальная. Ход урока I. Организационный момент. Учитель сообщает цели урока и план работы учащихся, обращая их внимание на то, что на уроке будут рассмотрены уравнения как из части В ЕГЭ по математике, так и возможные задания из части С. II. Запись домашнего задания. Каждый ученик получает индивидуальную карточку с домашним заданием. Часть заданий из Открытого банка заданий ЕГЭ по математике на сайте https://mathege.ru:8080/or/ege/Main, часть заданий составлена учителем (№6 и №7 у всех одинаковы). Пример одной из таких карточек: Домашнее задание Открытый банк заданий по математике на сайте http//:www.mathege.ru:8080/or/ege/Main каталог по заданиям В3
6х2log  и 4х – 3х2 принимают равные значения.
y = log  III. а) На досках заранее написаны решения уравнений. К доске вызываются по 1 ученику для поиска ошибок и правильного решения данного уравнения: 1) log 2 (- x) + log 2 (x2) = 3 2) lgx + lg (x + 3) = 1 3) log 5 x =  решений нет x + x + 3 = 1 log 5 x =  x = - 1 x = 5 
6log 2 x =  log 2 x = 11 x = 2 11 б) В это время с классом фронтально устная работа: решите уравнения:
В процессе обсуждения решений учитель ещё раз обращает внимание учащихся на необходимость выполнения проверки или учёта ОДЗ при решении уравнения (уравнение №3), а также на то, что принцип решения уравнения №7 и №8 одинаков, они отличаются только записью условия. Затем прослушиваются ответы у доски. Учащиеся с мест вносят коррективы и дополнения, если они необходимы. IV. Работа в группах. Класс заранее разделён на группы примерно одинаковые по уровню знаний. Каждая группа получает задание. Группе нужно предложить решение, записать в тетрадях и оформить решение на листе А1 (если нет документ – камеры). Учитель координирует работу групп. Задания для групп: I группа: Найдите все значения х, при каждом из которых выражения  и  принимают равные значения. II группа: Найдите нули функции у =ln2 (x2 +3x + 3) +  III группа: Найдите абсциссы точек пересечения графиков функций у =  и y =  IV группа: Найдите отрицательное значение а, при котором х = 4 является корнем уравнения log 4 (2x2 – xa – (a – 1)2) = 2 V группа: Найдите значение выражения 2х0 – 3у0, если (х0; у0) – решение системы 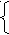 log 0,7 (1 – 12x + 3y) = 0log 5 (6y – 14x – 0,5) = - log 25 4 V. По окончании работы один учащийся от группы «защищает» решение перед другими группами (используется документ – камера, которая позволяет существенно сэкономить время. Если документ – камеры нет, то на доску с помощью магнитов прикрепляется лист А1 с оформленным решением ). Ученики других групп оформляют решения в тетрадях. VI. Самостоятельная работа на листочках. Каждому ученику (кроме очень слабых) выдаётся индивидуальное задание на карточке. Там одно из рассмотренных заданий, но не то, что было у его группы. Варианты заданий:
По окончании работы сдаются и проводится проверка через мультимедийный проектор. Пока класс работает по карточкам, учитель с очень слабыми учащимися проводит индивидуальную работу. Несколько человек работают на досках, несколько учеников могут работать за партами рядом с учителем. Примеры заданий для слабых учащихся: Решите уравнения:
VII. Итог урока. Учитель обращает внимание учащихся на то, что, несмотря на то, что в течение урока решались самые разнообразные задания, все они свелись к решению логарифмических уравнений. Выставление оценок. Использованные Интернет ресурсы: 1. https://mathege.ru:8080/or/ege/Main |
= 1
x · log 4
= log 4 7
· 2
и 
принимают равные значения?
и у = log
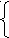lg(x2 + y2) = 1 + lg13
= - 2
(15 – 2x ) = - 1 4) log 0,2x + log 0,2(x+2) = log0,2 
= 2