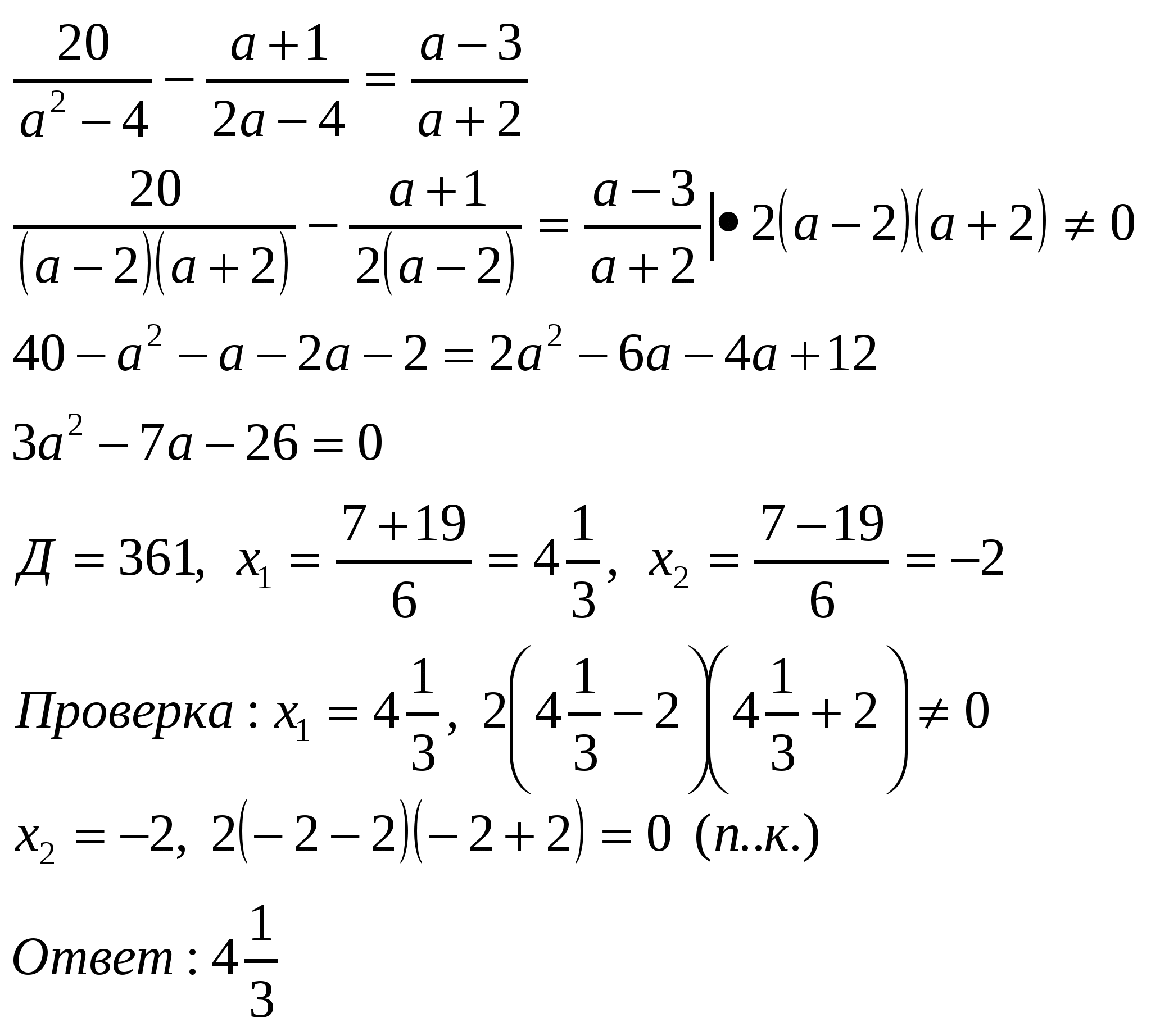|
Конспект урока решение дробно-рациональных уравнений фио (полностью) Попрыго Надежда Аннаньевна Место работы
ПЛАН-КОНСПЕКТ УРОКА
Решение дробно-рациональных уравнений
|
ФИО (полностью)
|
Попрыго Надежда Аннаньевна
|
|
Место работы
|
МБОУ ООШ №2
|
|
Должность
|
учитель
|
|
Предмет
|
математика
|
|
Класс
|
8 класс
|
|
Тема урока
|
Решение дробно-рациональных уравнений
Урок изучения нового материала
|
|
Базовый учебник
|
Макарычев Ю.Н. Алгебра. 8 класс: учеб. Для обучающихся общеобразовательных учреждений. М.:Мнемозина, 2010.
|
|
Технология
|
Технология развития критического мышления
|
Цель урока:
- обеспечить осознанное усвоение обучающимися алгоритма решения дробно-рациональных уравнений;
- активизировать мыслительную деятельность школьников через активное участие каждого в процессе работы.
Задачи урока:
- обучающие: расширить знания обучающихся об уравнениях, ввести понятие дробно-рационального уравнения, научиться применять алгоритм решения дробно-рациональных уравнений;
- развивающие: способствовать развитию аналитического мышления, формированию культуры чтения и речи;
- воспитательные: стимулировать самостоятельную деятельность, способствовать формированию коммуникативных навыков.
Тип урока: изучение нового материала.
Формы работы учащихся: индивидуальная, парная.
Приемы: «Кластер», «Верные - неверные утверждения», «Инсерт».
Оборудование: интерактивная доска.
Ход урока.
Этапы системно-деят.
|
Этапы урока
|
Деятельность учителя
|
Деятельность обучающихся
|
1. Мотивация к учебной деятельности
|
Вызов
|
Умение решать различные уравнения необходимо каждому школьнику. Сегодня мы расширим наши знания об уравнениях. А какие уравнения мы умеем решать?
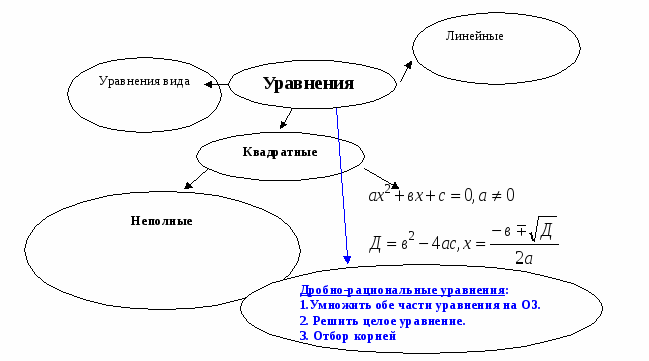
Составление кластера – учитель на доске с помощью учащихся
|
Учащиеся называют виды уравнений, которые умеют решать и способы их решения.
|
2.Актуализация опорных знаний
|
«Кластер»
|
3. Выявление места и причины затруднений
|
«Верные – неверные утверждения»
Верно ли, что:
Уравнение 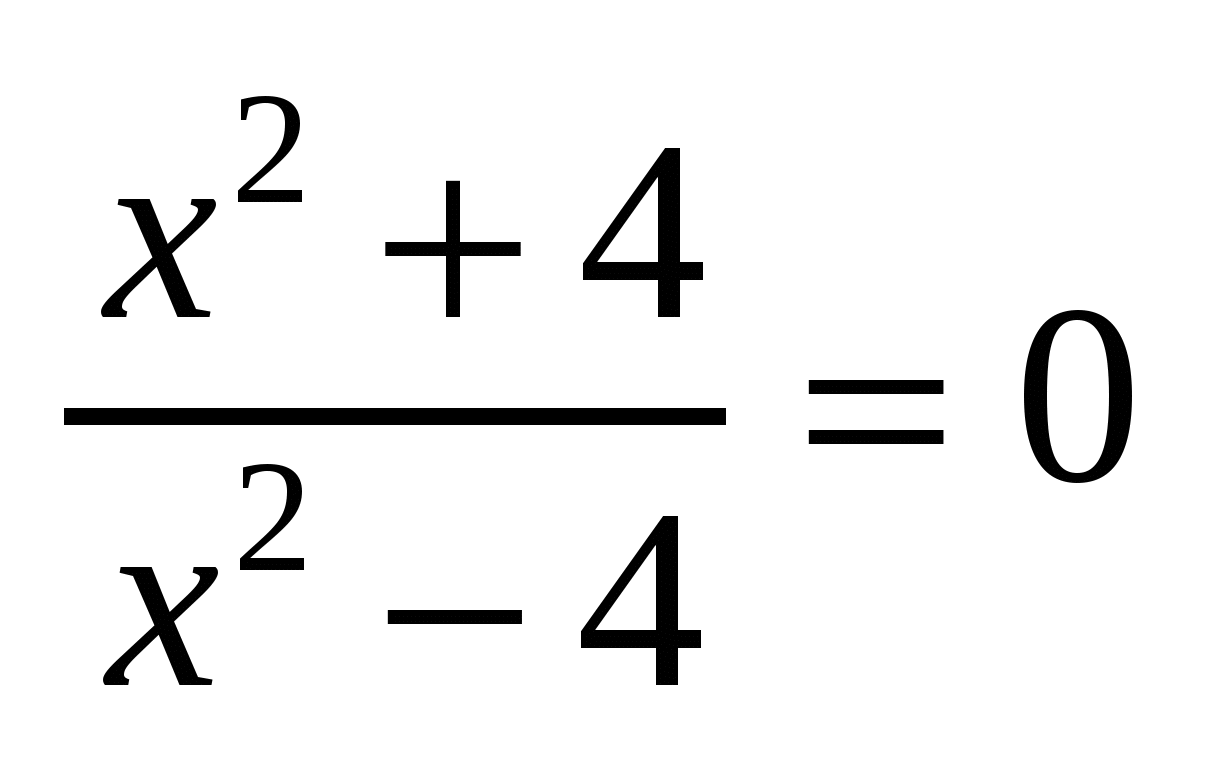 имеет корни -2 и 2 имеет корни -2 и 2
Уравнение 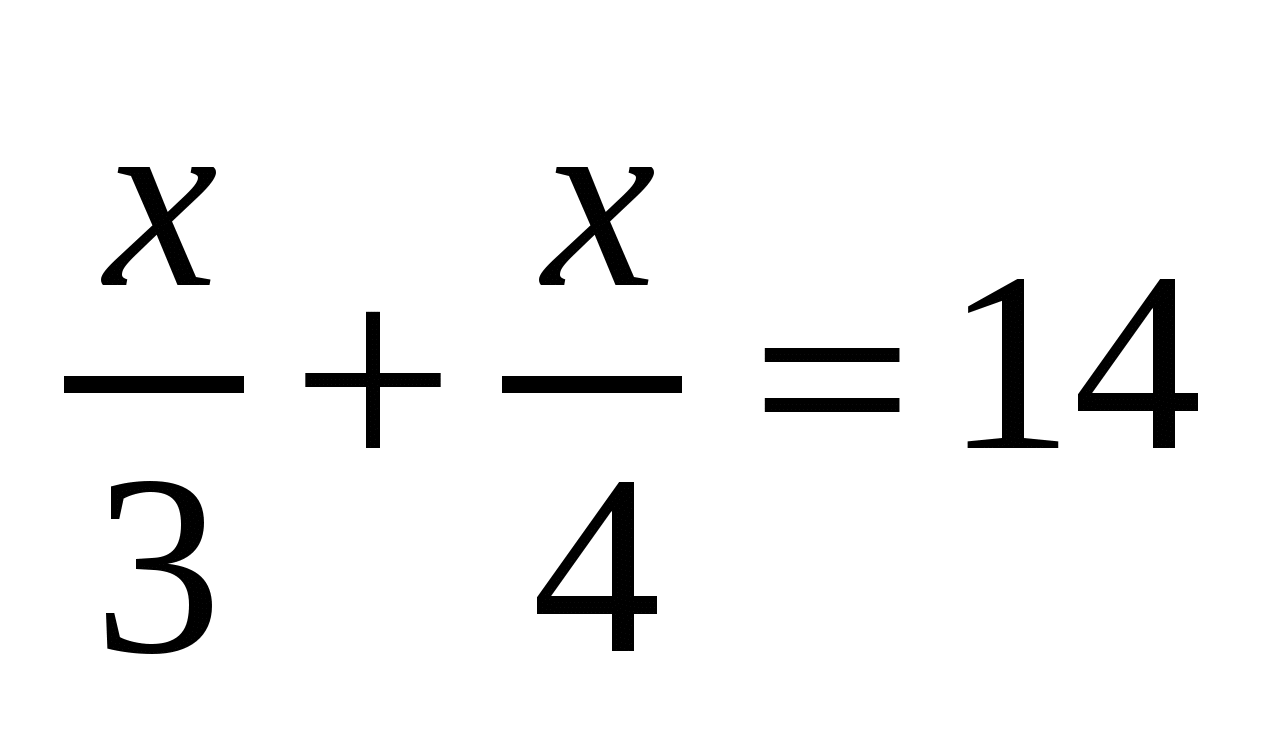 имеет корень 24 имеет корень 24
Уравнение 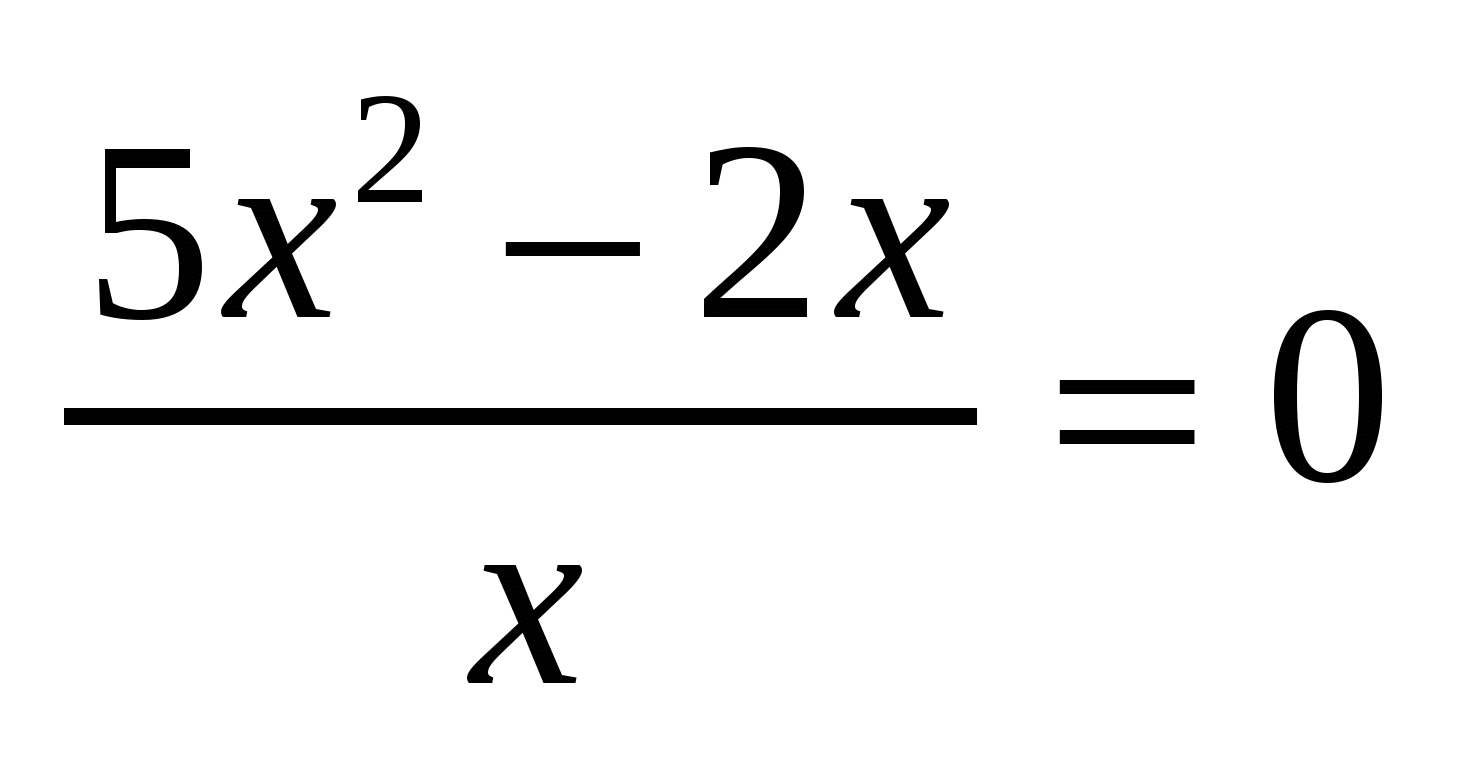 имеет корни 0 и 0,4 имеет корни 0 и 0,4
Уравнение 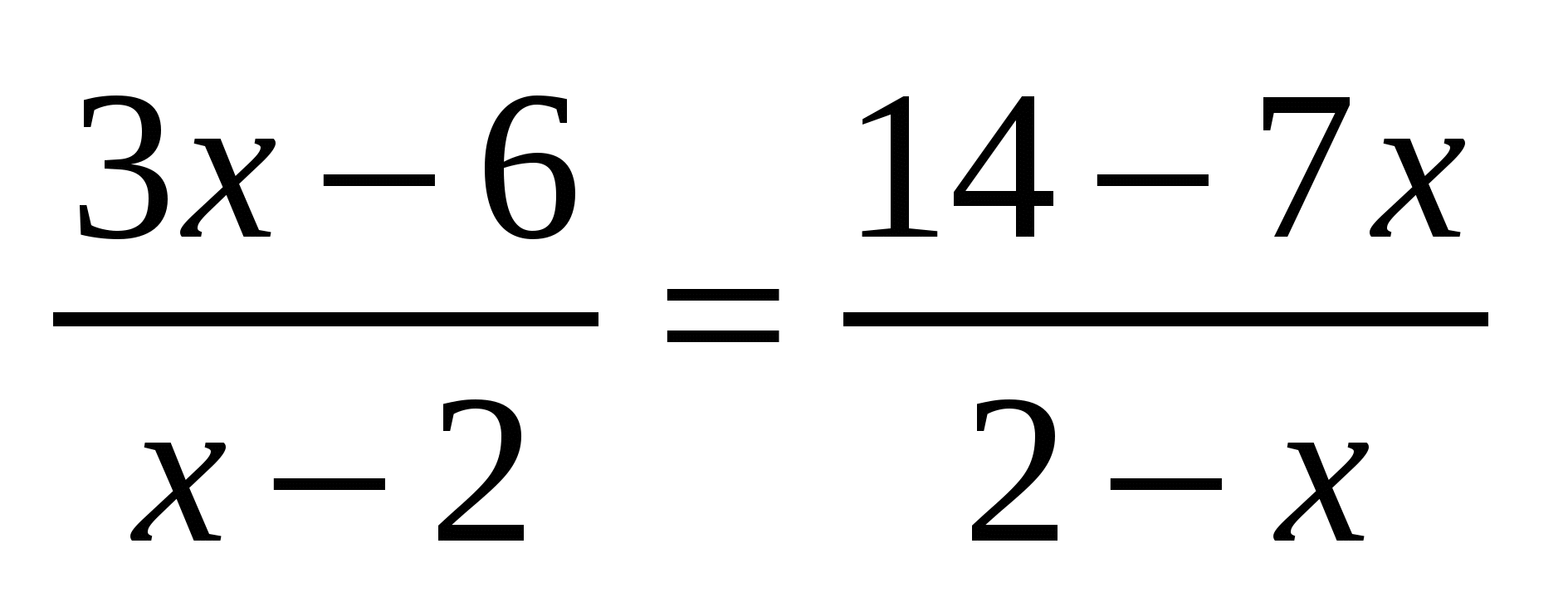 имеет корень 2 имеет корень 2
Уравнение 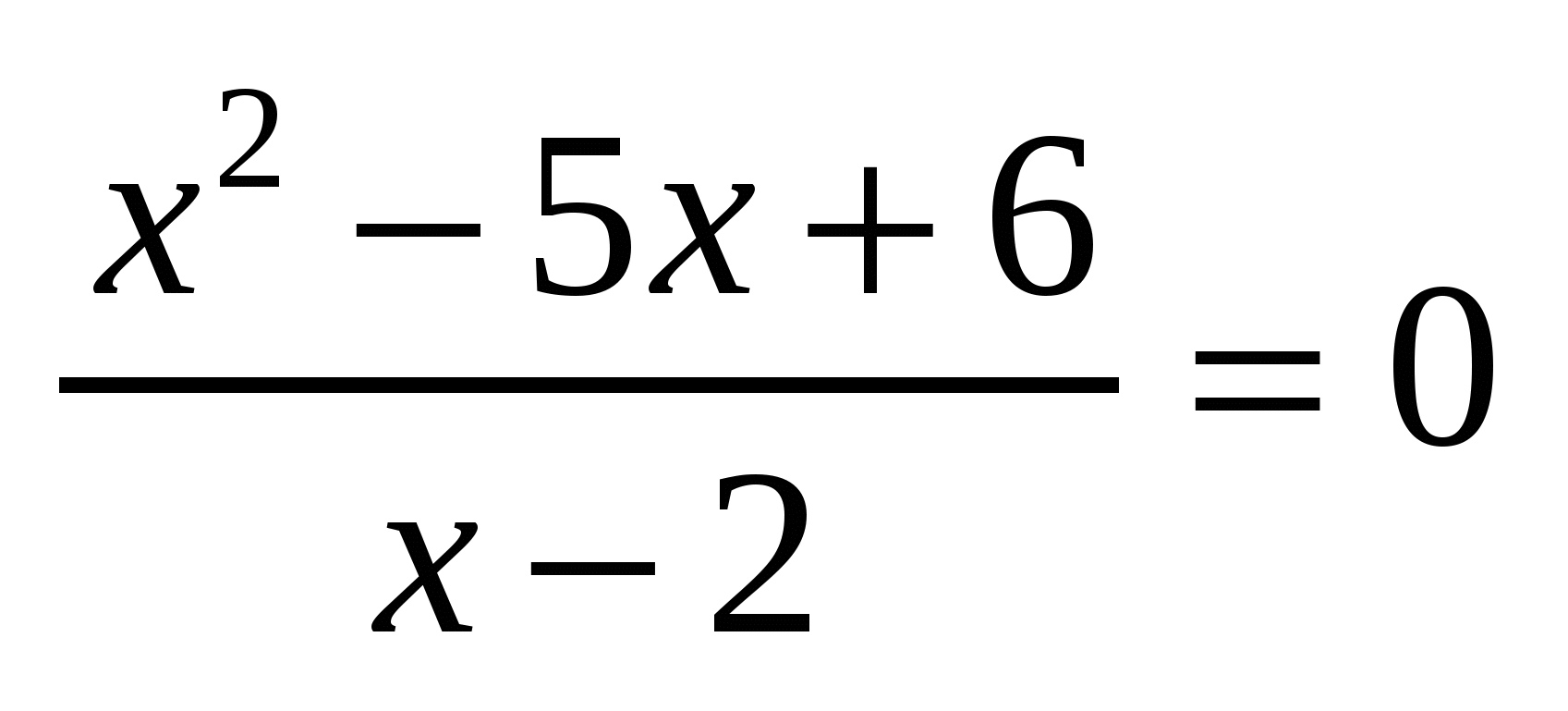 имеет корень 3 имеет корень 3
Проверяем ответы, на доске учитель заполняет таблицу
|
Учащиеся решают в тетрадях уравнения, работают в парах.
Учащиеся отвечают на вопросы задания, в тетрадях верные ответы отмечают знаком «+», неверные «-»
|
4. Построение проекта выхода из затруднений
|
Осмысление
|
«Инсерт»
Учащиеся работают с текстом п.34.
|
Учащиеся читают текст учебника, делают отметки «+» - знаю, «√»- новое, «?» – ничего не понял. Обсуждают в парах ответы на предыдущее задание.
|
Беседа по прочитанному тексту:
- Что вам было известно?
- Что новое узнали?
- Что непонятно?
- С каким видом уравнений познакомились?
|
Учащиеся отвечают на вопросы.
Дополняют кластер «Дробно-рациональные уравнения».
Возвращаемся к заданиям «Верно ли, что…?»
|
|
№1
|
№2
|
№3
|
№4
|
№5
|
+
|
+
|
+
|
+
|
-
|
-
|
+
|
-
|
-
|
+
|
|
Учащиеся высказывают иное мнение о корнях уравнений
|
5. Реализация построенного проекта, алгоритма
|
Рефлексия
|
Ответы на вопросы по заданию:
1.Объясните причину того, что числа -2 и 2 не являются корнями уравнения?
2.Прокомментируйте решение второго уравнения.
3. Почему после прочтения текста изменилось ваше мнение о корнях 3-го уравнения?
4. Найдите в тексте подтверждение того, что число 2 не является корнем уравнения.
5. Сформулируйте алгоритм решения 5-го уравнения.
|
Учащиеся отвечают на вопросы, опираясь на текст учебника, формулируют алгоритм решения дробно-рациональных уравнений, записывают в тетради:
1.Умножить обе части уравнения на общий знаменатель.
2.Решить целое уравнение
3.Отбор корней (знаменатель не равен нулю)
|
6. Первичное закрепление во внешней речи
|
Учащимся предлагается проанализировать готовое решение уравнения:
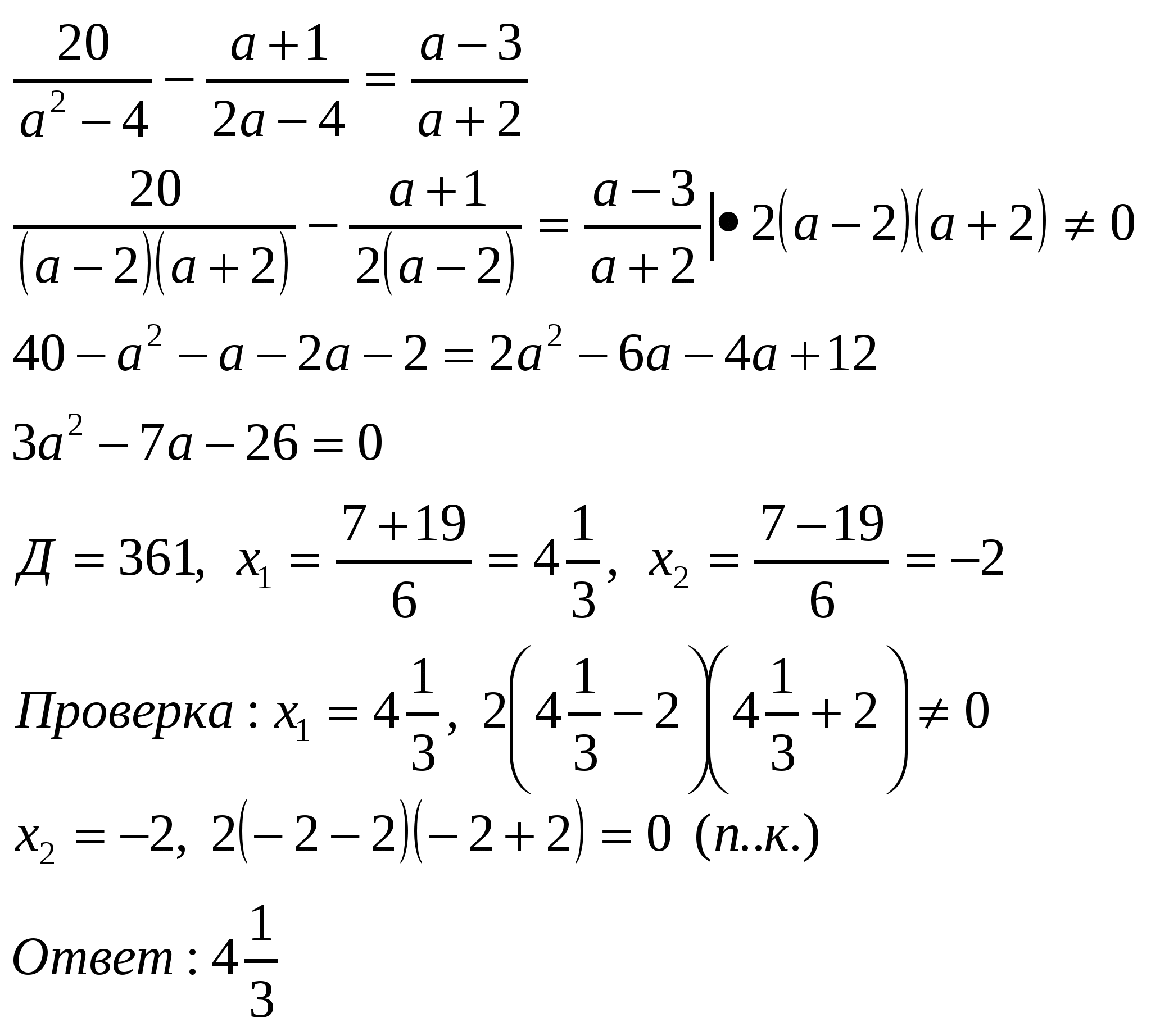
|
Учащиеся обсуждают в парах решение, комментируют решение, опираясь на алгоритм.
|
Решить уравнение из учебника №769(а)
|
№769 (а) ученик решает на доске
|
7. Самостоятельная работа с самопроверкой по эталону
|
Закрепление
|
Решить уравнения из учебника: №769 (б), 770(а, г).
Учитель контролирует решение, оказывает помощь.
|
Учащиеся решают уравнения в парах, проверка решения №769 (б) по готовому решению.
|
8. Включение в систему знаний
|
|
Составить задачу, при решении которой получилось уравнение: 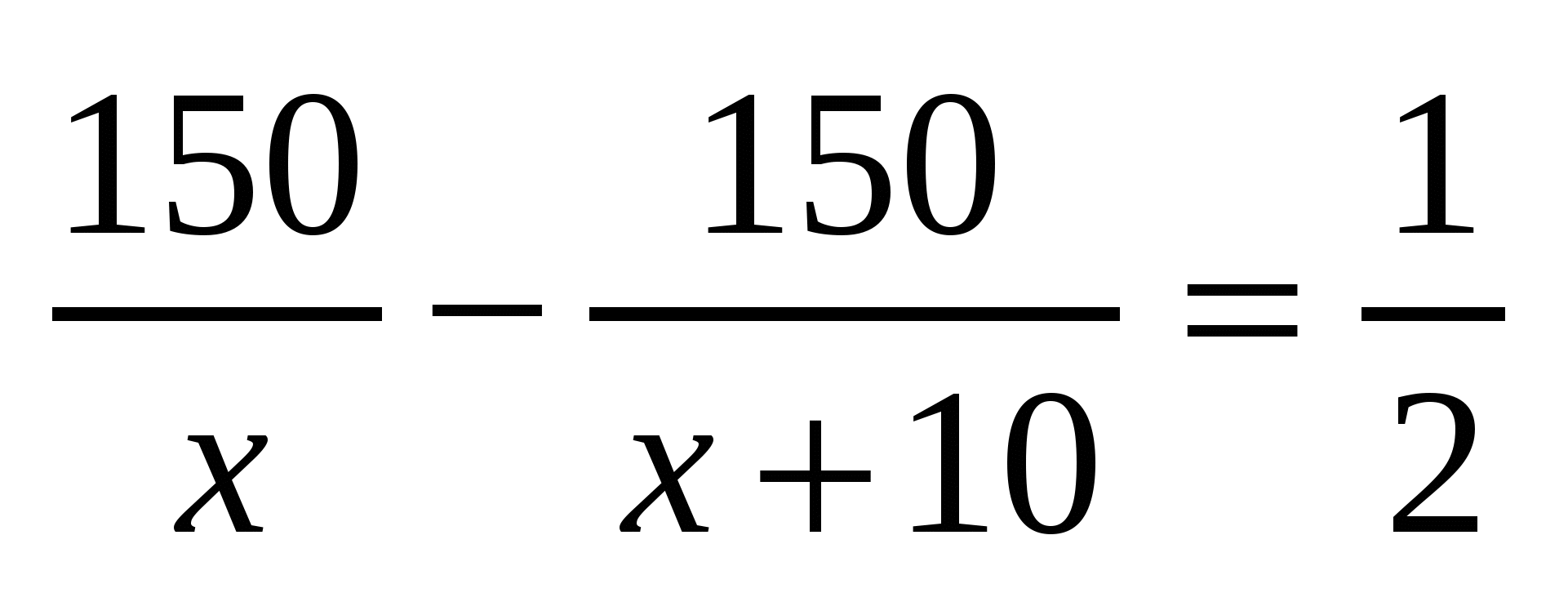
|
Учащиеся составляют задачу. Например:
«Из поселка в город, до которого 150 км, отправились одновременно грузовой и легковой автомобиль. Скорость легкового автомобиля на 10км/ч больше скорости грузового, и поэтому он затратил на весь путь на 0,5ч меньше времени, чем грузовой. Найти скорость грузового автомобиля.
Решают уравнение.
|
9. Рефлексия учебной деятельности
|
|
Подведение итогов урока.
Для чего нужны дробно-рациональные уравнения?
|
1.Сегодня на уроке я узнал ….
2. На уроке составили …
3. Запомнил, что ….
|
|
Домашнее задание
|
п.34, алгоритм решения дробно-рациональных уравнений. №769 (в), 770 (б, д), 780 (а, в)
|
|
Учебные ситуации
Краткая аннотация учебной ситуации
|
Вид учебной ситуации
|
Планируемые результаты изучения темы для учебной ситуации
|
Формируемые УУД (личностные, регулятивные, познавательные, коммуникативные)
|
Повторение - какие уравнения и способы их решения нам известны
|
|
Личностные – умение ясно, точно, грамотно излагать свои мысли в устной речи
Метапредметные – понимание сущности алгоритмических предписаний
Предметные - овладение приемами решения уравнений
|
Личностные – действие смыслообразования
Регулятивные – оценка, коррекция
Познавательные - структурирование знания, осознанное построение речевого высказывания в устной и письменной форме, обобщение, классификация
Коммуникативные – владение монологической и диалогической формами речи.
|
«Верные – неверные утверждения»
Верно ли, что корнем уравнение является число?
|
Ситуация – проблема
|
Личностные – критичность мышления,
Метапредметные – анализ материала
Предметные – умение решать уравнения
|
Личностные – действие смыслообразования
Регулятивные – целеполагание, саморегуляция
Познавательные – анализ, самостоятельное создание алгоритмов деятельности при решении уравнений
Коммуникативные – планирование учебного сотрудничества со сверстниками, управление поведением партнера
|
Работа с текстом учебника и обсуждение прочитанного
|
|
Личностные – умение понимать смысл поставленной задачи, критичность мышления
Метапредметные – умение находить информацию, необходимую для решения математических проблем и представлять ее в понятной форме, умение планировать деятельность.
Предметные – умение работать с математическим текстом
|
Личностные – действие смыслообразования
Регулятивные – планирование, контроль, коррекция, оценка
Познавательные – смысловое чтение, определение основной и второстепенной информации; анализ, синтез
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли
|
Анализ решения дробно-рационального уравнения
|
Ситуация – оценка
|
Личностные – критичность мышления, умение контролировать процесс и результат математической деятельности
Метапредметные – понимание сущности алгоритмических предписаний
Предметные – овладение приемами решения дробно-рациональных уравнений
|
Личностные – действие смыслообразования
Регулятивные – контроль и оценка
Познавательные – осознанное построение высказывания в устной и письменной форме, анализ
Коммуникативные – владение монологической речью
|
Решение уравнений из учебника
|
Ситуация-тренинг
|
Личностные – умение контролировать процесс и результат учебной математической деятельности, критичность мышления
Метапредметные - понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом
Предметные – овладение методами решения дробно-рациональных уравнений
|
Личностные – самоопределение и действие смыслообразования
Регулятивные – целеполагание, планирование, коррекция
Познавательные – обобщение и аналогия, осознанное построения речевого высказывания в письменной речи, контроль и оценка результатов деятельности
Коммуникативные – планирование учебного сотрудничества с учеником, управление поведением партнера
|
Составить задачу по заданному уравнению
|
Ситуация - иллюстрация
|
Личностные – критичность мышления, умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи
Метапредметные – умение видеть математическую задачу в окружающей жизни
Предметные – представление об уравнении, как математической модели, описывающей реальные события
|
Личностные – действие нравственно-этического оценивания усваиваемого содержания
Регулятивные – контроль
Познавательные – моделирование и преобразование модели, анализ, установление причинно-следственных связей,
Коммуникативные – умение с достаточной полнотой и точностью выражать свои мысли
| |
|
|
 Скачать 97.88 Kb.
Скачать 97.88 Kb.