«Свойства числовых неравенств»
 Скачать 39.95 Kb.
|
| Методическая разработка урока алгебры в 8 классе. Тема: «Свойства числовых неравенств». Образовательные цели: изучить свойства числовых неравенств, учить их применять. Развивающие: развивать гибкость мышления (через умение находить различные способы решения поставленной задачи); самостоятельность, рациональность (учить выбирать оптимальный способ решения задачи, обосновать избираемый метод решения), критичность (через самоконтроль своей деятельности), работать над развитием речи. Воспитательные: воспитывать интерес к предмету, умение вести диалог, умение работать с одноклассниками. Тип урока: урок «открытия» нового знания. Методы: объяснительно – иллюстративный, частично – поисковый, проблемный. Формы работы: фронтальная, индивидуальная, парная. Приёмы учебной деятельности: работа с учебником, формулировка суждений и умозаключений, конкретизация, сравнение. План урока. 1.Организационный момент. 2.Актуализация знаний . 3.Изучение нового. 4.Проверка понимания учащимися нового материала и первичное закрепление. 5.Домашнее задание. 6. Подведение итогов урока. Ход урока.
«Из двух чисел меньше то, изображение которого на числовой прямой расположено …» « Из двух чисел больше то, изображение которого на числовой прямой расположено …»
а) к обеим частям неравенства – 1 < 4 прибавить число 5; – 2. б) известно, что a < b, поставьте знак больше или меньше так, чтобы получилось верное неравенство a – 4 ? b – 4 ; b + 6 ? a + 6; 12 – a ? 12 – b в) сравните с нулём числа а и b, если известно, что a + 5 > b + 5 b>2 ; a – 1 < b – 1 b <1 – 0,1 г) расположите в порядке возрастания числа a + 8; b – 4; a + 3; a; b – 1; b, если известно, что a > b Вспомним, какие свойства используются при решении уравнений.
Возможно, это свойство справедливо и для числовых неравенств? Задание учащимся: Дано: a > b; b > 0 1. Умножьте обе части неравенства на ( b – a ) a( b – a ) > b( b – a ) 2.Раскройте скобки ab - a² > b² – ab 3.Вычесть из левой и правой части неравенства ab – a² ( преобразовать так, чтобы в левой части был нуль) ab – a² – ab + a² > b² – ab – ab + a² 4. Привести подобные слагаемые 0 > b² – 2ab + b² 0 > ( b – a )² 5.Но мы знаем, что ( b – a )², где b ≠ a число положительное Перед вами стоит задача: выяснить, как пришли к неверному результату? Проверка снизу вверх. По - видимому ошибка допущена при умножении обеих частей неравенства на ( b – a ). Чтобы ответить на вопрос: Почему получили неверный результат? Нам нужно изучить ещё одно свойство числовых неравенств. Доказательство теоремы 4 учащиеся проводят самостоятельно с помощью учебника. Вариант 1 – умножение на положительное число Вариант 2 – умножение на отрицательное число Теоремы доказываются учащимися всему классу. Работа оценивается. Применяем изученное свойство.
а) Умножьте обе части на 2; – 3 б) Разделите обе части неравенства на 5; – 1
а) к обеим частям неравенства прибавить 2 б) из обеих частей неравенства вычесть 7 в) обе части неравенства умножить на 2 г) умножить на – 3 д) разделить на 4 е) разделить на – 2 Ответы записываются учащимися в тетрадях, затем проверка.
a – 2 ? b – 2 3a ? 3b – 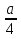 ? –  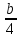b + 3 ? a + 3 – 2a ? – 2b
7a < 2a 5a > 3a – 3a < 3a – 5a > 2a Решить №752,753. Подведение итогов урока 1.С какими новыми свойствами числовых неравенств познакомились? 2. Что из изученного ранее применяли сегодня? Домашнее задание: п.29, №719,755 |
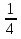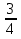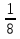и 
; 
и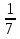 
; 19,1 и19,09. Какое число из каждой пары лежит правее на числовой оси?