Результаты изучения учебного предмета
Изучение математики в 7 классе направлено на достижение обучающимися личностных, метапредметных (регулятивных, познавательных и коммуникативных) и предметных результатов.
1. В направлении личностного развития:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений,
рассуждений.
2. В метапредметном направлении:
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные
стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии
с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
3. В предметном направлении:
предметным результатом изучения курса является сформированность следующих умений:
Знать, какая фигура называется отрезком; уметь обозначать точки и прямые на рисунке, изображать возможные случаи взаимного расположения точек и прямых, двух прямых, объяснить, что такое отрезок, изображать и обозначать отрезки на рисунке.
Объяснить, что такое луч, изображать и обозначать лучи, знать какая геометрическая фигура называется углом, что такое стороны и вершины угла, обозначать неразвёрнутые и развёрнутые углы, показывать на рисунке внутреннюю область неразвёрнутого угла, проводить луч, разделяющий его на два угла;
Какие геометрические фигуры называются равными, какая точка называется серединой отрезка, какой луч называется биссектрисой угла; сравнивать отрезки и углы, записывать результаты сравнения, отмечать с помощью масштабной линейки середину отрезка, с помощью транспортира проводить биссектрису угла;
Измерить данный отрезок с помощью масштабной линейки и выразить его длину в сантиметрах, миллиметрах, метрах, находить длину отрезка в тех случаях, когда точка делит данный отрезок на два отрезка, длины которых известны;
Что такое градусная мера угла, находить градусные меры углов, используя транспортир, изображать прямой, острый, тупой и развёрнутый углы;
Какие углы называются смежными и чему равна сумма смежных углов, какие углы называются вертикальными и каким свойством обладают вертикальные углы, какие прямые называются перпендикулярными; уметь строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке смежные и вертикальные углы;
Объяснить, какая фигура называется треугольником, и назвать его элементы; что такое периметр треугольника, какие треугольники называются равными, формулировку и доказательство первого признака равенства треугольников;
Определения перпендикуляра, проведённого из точки к данной прямой, медианы, биссектрисы, высоты треугольника, равнобедренного и равностороннего треугольников; знать формулировку теорем о перпендикуляре к прямой, о свойствах равнобедренного треугольника;
Формулировки и доказательства второго и третьего признаков равенства треугольников;
Определение окружности, уметь объяснить, что такое центр, радиус, хорда, диаметр, дуга окружности, выполнять с помощью циркуля и линейки простейшие построения: отрезка, равного данному; угла, равного данному; биссектрисы данного угла; прямой, проходящей через данную точку и перпендикулярную к данной прямой; середины данного отрезка;
Определение параллельных прямых, названия углов, образующихся при пересечении двух прямых секущей, формулировки признаков параллельности прямых; понимать, какие отрезки и лучи являются параллельными; уметь показать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности двух прямых;
Аксиому параллельных прямых и следствия из неё; доказывать свойства параллельных прямых и применять их при решении задач;
Доказывать теорему о сумме углов треугольника и её следствия; знать какой угол называется внешним углом треугольника, какой треугольник называется остроугольным, прямоугольным, тупоугольным;
Доказывать теорему о соотношениях между сторонами и углами треугольника и следствия из неё, теорему о неравенстве треугольника, применять их при решении задач;
Доказывать свойства прямоугольных треугольников, знать формулировки признаков равенства прямоугольных треугольников и доказывать их, применять свойства и признаки при решении задач;
Какой отрезок называется наклонной, проведённой из данной точки к данной прямой, что называется расстоянием от точки до прямой и расстоянием между двумя параллельными прямыми; уметь строить треугольник по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трём сторонам.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Используемые формы, способы и средства проверки и оценки результатов обучения.
Письменный контроль (самостоятельные и контрольные работы, проверка домашнего задания);
Тестовый (тестирование);
Устный опрос (собеседование, зачет)
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
В рабочей программе предусмотрено 6 контрольных работ по темам:
Перечень контрольных работ
Контрольная работа №1 «Измерение отрезков и углов»
Контрольная работа №2 «Треугольники»
Контрольная работа №3 «Параллельные прямые»
Контрольная работа №4 «Соотношения между сторонами и углами треугольника»
Контрольная работа №5 «Прямоугольные треугольники. Построение треугольника по трем элементам»
Итоговая контрольная работа №6
Приложение 1
Контрольная работа№1 по геометрии «Начальные геометрические сведения»
Вариант 1
Три точки В, С и Д лежат на одной прямой. Известно, что ВД — 17 см, ДС = 25 см. Какой может быть длина отрезка ВС?
Сумма вертикальных углов МОЕ и ДОС, образованных при пересечении прямых МС и ДЕ, равна 204°. Найдите угол МОД.
С помощью транспортира начертите угол, равный 78°, и прове�дите биссектрису смежного с ним угла.
Контрольная работа№1 по геометрии «Начальные геометрические сведения»
Вариант 2
Три точки М, N и К лежат на одной прямой. Известно, что МN = 15 см, NК = 18 см. Каким может быть расстояние МК?
Сумма вертикальных углов АОВ и СОД, образованных при пе�ресечении прямых АД и ВС, равна 108°. Найдите угол ВОД.
С помощью транспортира начертите угол, равный 132°, и про�ведите биссектрису одного из смежных с ним углов.
Контрольная работа№2 по геометрии «Треугольники»
Вариант 1
1). На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что 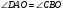 . .
С
А O
В
D
2). Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АDВ = АDВ =  АDС . Докажите, что АВ = АС . АDС . Докажите, что АВ = АС .
3). В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2 . Найдите стороны треугольника.
Контрольная работа№2 по геометрии «Треугольники»
Вариант 2
1). На рисунке 1 отрезки МЕ и РК точкой D делятся пополам. Докажите, что  КМD = КМD =  РЕD. РЕD.
М К
D
Р Е
2). На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ . Докажите, что луч DР – биссектриса угла МDК .
3). В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3 . Найдите стороны треугольника.
Контрольная работа№3 по геометрии «Параллельные прямые»
1 вариант.
1). Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ // QF.
2). Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если 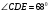 . .
3). На рисунке АС // ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка CD.
D
M
A B
C
Контрольная работа№3 по геометрии «Параллельные прямые»
2 вариант.
1). Отрезки МN и ЕF пересекаются в их середине Р. Докажите, что ЕN // МF.
2). Отрезок AD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне FD и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если 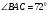 . .
3). На рисунке AB // DC, АВ = DC. Докажите, что точка О – середина отрезков АС и ВD.
В С
О
А D
Контрольная работа№4 по геометрии «Соотношения между сторонами и углами треугольника»
1 вариант.
1). На рисунке:  . Найдите сторону АВ треугольника АВС. . Найдите сторону АВ треугольника АВС.
Е
B М
А
C D
F
2). В треугольнике СDE точка М лежит на стороне СЕ, причём 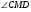 - острый. Докажите, что DE > DM. - острый. Докажите, что DE > DM.
3). Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Контрольная работа№4 по геометрии «Соотношения между сторонами и углами треугольника»
2 вариант.
1). На рисунке:  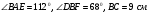 . Найдите сторону АС треугольника АВС. . Найдите сторону АС треугольника АВС.
Е М
A С
В
D F
2). В треугольнике MNP точка К лежит на стороне MN, причём 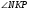 - острый. Докажите , что КР < МР. - острый. Докажите , что КР < МР.
3). Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа№5 по геометрии «Соотношения между сторонами и углами треугольника»
1 вариант.
1). В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NK в точке О, причём ОК = 9 см. Найдите расстояние от точки О до прямой МN.
2). Постройте прямоугольный треугольник по гипотенузе и острому углу.
3). Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу .
Контрольная работа№5 по геометрии «Соотношения между сторонами и углами треугольника»
2 вариант.
1). В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причём FC = 13 см. Найдите расстояние от точки F до прямой DE.
2). Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
3). В треугольнике АВС  , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС. , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.
Итоговая контрольная работа
Вариант 1
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ. На ней взята точка К. Докажите равенство треугольников АВК и СВК.
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса СК. Найдите углы треугольника АВС, если угол АКС = 60°.
Постройте прямоугольный треугольник по катету и противолежащему углу.
Итоговая контрольная работа
Вариант 2
В равнобедренном треугольнике АВС с основанием АС и углом при вершине В, равным 36°, проведена биссектриса АК. Докажите , что треугольники СКА и АКВ равнобедренные.
В
36°
К
А С
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВМ. На ней взята точка К. Докажите равенство треугольников АМК и СМК.
Постройте прямоугольный треугольник по катету и прилегающему углу.
СОГЛАСОВАНО
Протокол заседания методического совета МБОУ Селивановская СОШ
от_______ _____ года №_1_
Председатель МС
______________/Пушкарёва Н.В./
(подпись) Ф.И.О.
СОГЛАСОВАНО
Заместитель директора по УР
__________________/Пушкарёва Н.В./ (подпись) Ф.И.О.
20 года
дата
|
 Скачать 0.73 Mb.
Скачать 0.73 Mb.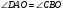 .
. АDВ =
АDВ =  АDС . Докажите, что АВ = АС .
АDС . Докажите, что АВ = АС . КМD =
КМD =  РЕD.
РЕD.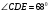 .
.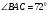 .
. . Найдите сторону АВ треугольника АВС.
. Найдите сторону АВ треугольника АВС.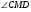 - острый. Докажите, что DE > DM.
- острый. Докажите, что DE > DM.
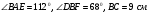 . Найдите сторону АС треугольника АВС.
. Найдите сторону АС треугольника АВС. 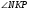 - острый. Докажите , что КР < МР.
- острый. Докажите , что КР < МР. , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.
, биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.