Забельникова Ольга Васильевна. Место работы и должность: мбоу-сош №4 города Тулы, учитель математики. Образование: высшее, тгпи им. Л. Н. Толстого, 1982г., диплом
 Скачать 464.62 Kb. Скачать 464.62 Kb.
|
| Тема: « Признаки делимости » (учебный комплект под редакцией Г.В.Дорофеева) 1, Найдите сумму цифр каждого числа: 361; 1284; 432; 2889, а). Какие из указанных чисел делятся на 3? б). Какие из указанных чисел делятся на 9? 2. Поставьте вместо * такую цифру, чтобы полученное число делилось на 3. 1*9. Делится ли полученное число на 9? ИПМ 8.2. Индивидуальные карточки-тесты для 11 класса. (Приложение). Тема: « Координаты точки и координаты вектора». (Геометрия 10-11 под редакцией Л.С.Атанасяна).
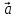 = =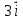 +2 +2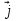 -5 -5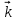 ; ;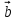 = =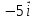 +3 +3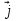 - -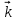 ; ;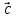 = =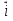 - -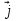 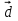 = =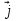 + +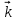 ; ;2. Для векторов 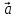 {5;-1;2}; {5;-1;2};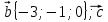 {0;-1,0} {0;-1,0} запишите разложение этих векторов по координатным векторам 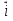 ; ;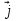 ; ;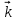 ; ;ИПМ 8.3. Индивидуальные карточки-тесты для 7 класса. (Приложение). Тема: «.Линейная функция и ее свойства» (Алгебра -7 под редакцией С.А.Теляковского).
у = Зх + 4; у = - 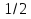 х; у = х; у = 5- 2х; у = 4; у = 6х. х; у = х; у = 5- 2х; у = 4; у = 6х.
а) у = Зх; б)у=-х; в) у = х; г) у= 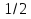 х хИПМ 8.4. Индивидуальные карточки с ошибкой в решении. (Приложение) Тема: « Решение неравенств 2-ой степени »(Алгебра-9 под редакцией С.А.Теляковского). Обязательное задание. Решите неравенство: 2х2-13х + 16 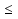 0 0 1). Рассмотрим функцию f(x)= 2 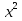 -13х+16; х -13х+16; х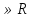 . График парабола, ветви . График парабола, ветвинаправлены вверх. 2). Выясним взаимное расположение графика этой функции и оси х. Для этого найдем нули функции: f(x)= 0 , если 2х2 - 13х +16 = 0 D = 169-4  2 2 16 = 169-144 = 25- две точки пересечения с осью абсцисс. 16 = 169-144 = 25- две точки пересечения с осью абсцисс.13- 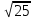 13+ 13+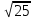 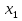 =----------- = 2; х2 =-------- = 7. =----------- = 2; х2 =-------- = 7.4 4 Изобразим схематично график функции f(x)=2х2–13х+16.  f(x) f(x)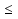 0, если х 0, если х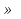 [2;7]. [2;7].Дополнительное задание. Решите неравенство: (х-4)(5-х) 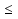 0. 0.Решение: (х-4)(5-х) 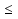 0; 0;-(х-4)(х-5) 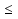 0; 0;(х-4)(х-5) 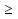 0; 0;Числа 4; 5 - нули функции f(x)=(х-4)(х-5), разбивают ООФ на интервалы, внутри которых функция сохраняет знак, при переходе через "нуль" функции знаки чередуются. 4 5 х 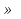 ( (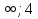 ) )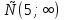 . .ИПМ 8.5. Индивидуальные карточки по математике для 6 класса. (Приложение). Тема; «Вычитание рациональных чисел». 1) Выполните вычитание: а)-5-(-3); б) 3,95-4; в) 6,34 - (-1,66). 2) Решите уравнение: y-3,96=-2 3) Найдите расстояние между точками A(- 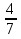 );B(- );B(-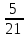 ) )Примечание: решение первого задания оценивается 3-мя баллами, решение каждого следующего добавляет по 1 баллу. ИПМ 8.6.Индивидуальные карточки по геометрии для 11 класса. (Приложение). Тема: «Простейшие задачи в координатах». 1) Вычислите угол между векторами 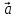 {2:-2;0} и {2:-2;0} и 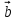 {3;0;3}. З балла. {3;0;3}. З балла.2) Вычислите углы между вектором 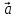 {2;1;2} и координатными векторами. {2;1;2} и координатными векторами.4 балла. 3) Точки А(1;-1;3); В(3;-1;1); С(-1;1;3) - вершины треугольника. Найдите углы треугольника и его площадь. 5 баллов. ИПМ 9.Разноуровневые самостоятельные работы. Цели:- помочь учащимся самостоятельно разобраться в изучаемом материале (обучающие);
Содержание самостоятельных работ:
Виды самостоятельных работ:
Для работы используются:
Проверка осуществляется по желанию учителя:
ИПМ 9.1. Контролирующая самостоятельная работа по алгебре в 9 классе. (Приложение). Тема: « Решение неравенств методом интервалов » Обязательная часть
2.(х + 2)(х-8)+ 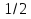 )<0; )<0; 3.х(х + 1,2)(х-6)>0; Дополнительная часть 4. (х + 5)(9-х)(4х + 12) 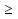 0; 0; 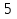 . .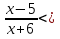 0 0
ИПМ 9.2. Обучающая самостоятельная работа по геометрии в 8 классе (4-х вариантная). Тема урока: «Теорема Пифагора) 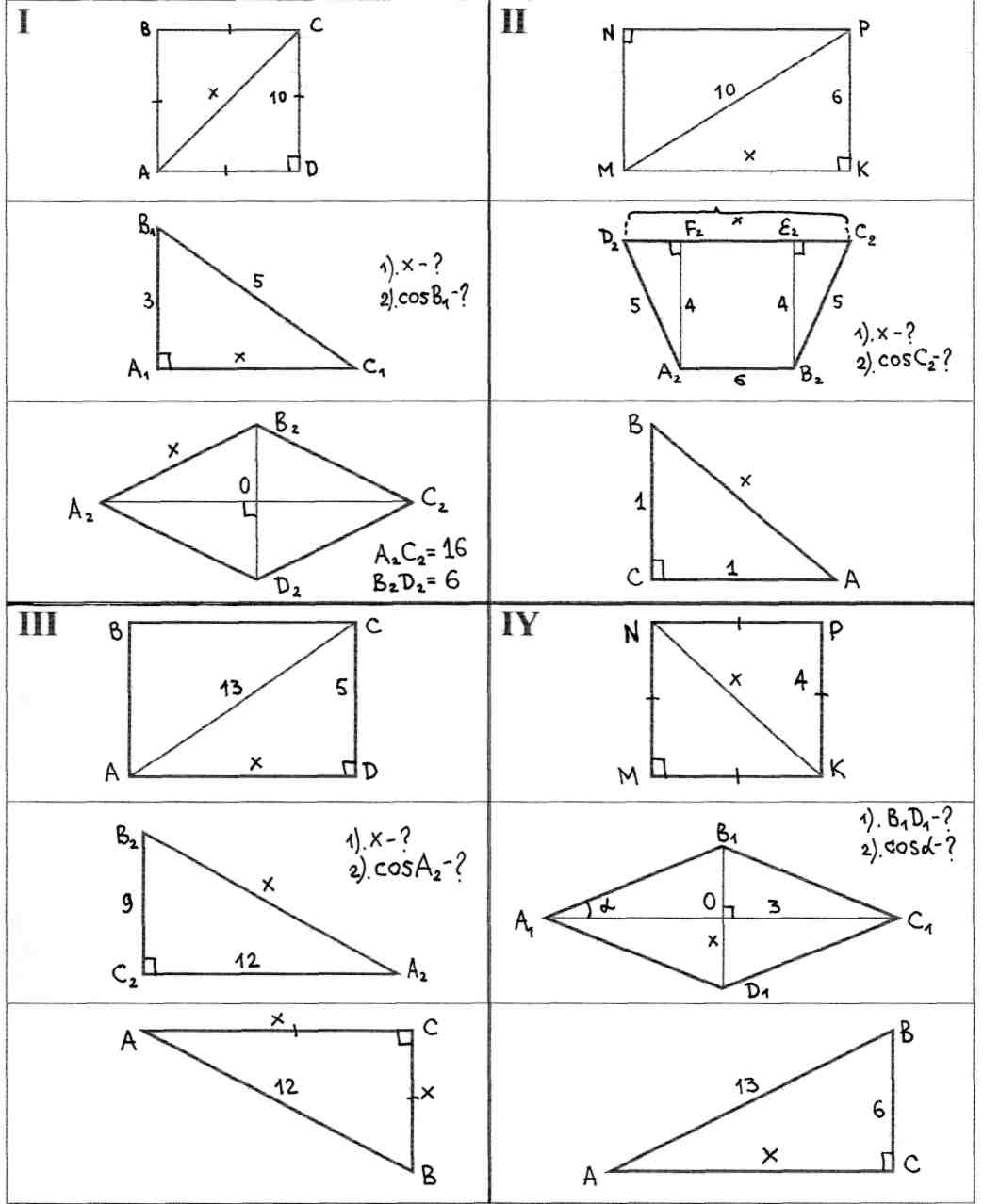 ИПМ 10. Дифференцированные контрольные работы. Цели: - контроль уровня усвоения школьниками учебного материала;
- выявление пробелов в знаниях учащихся с целью их дальнейшей корректировки. Основной принцип; - предъявление ученику минимальных требований. Ученик понимает: это я обязан сделать, а дальше - если могу и хочу. Структура контрольной работы:
Специфика проведения:
Важнейшее условие повышения качества знаний - анализ и дополнительная проработка неусвоеннного материала. ИПМ 10.1 Дифференцированная контрольная работа по математике в 6 классе (Приложение) Тема: "Дроби и проценты" Вариант II Обязательная часть. Вычислите: 1) 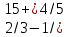 ; ;2) 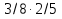 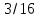
черно-белые. Сколько черно-белых фотографий в альбоме?
15 45 100 ' 100
Дополнительная часть 7. Расположите величины в порядке возрастания: 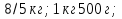 1400г;425г. 1400г;425г. 8. Коля сначала раскрасил 28 флажков, что составило 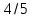 всех имевшихся у него всех имевшихся у негофлажков. Потом он раскрасил треть оставшихся флажков. Сколько флажков еще не раскрашено? Какую часть всех флажков составляют нераскрашеные флажки? Критерий оценок
ИПМ 10.2 Дифференцированная контрольная работа по алгебре и началам анализа в 11 классе. (Приложение) Тема: "Первообразная и интеграл" Обязательная часть. 1. Докажите, что функция F есть первообразная для функции f на промежутке ( - 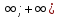 ) )F(х) =х3-2х+1, f(х) =Зх2-2 2. Для функции fх)=4 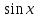 найдите: найдите:а) множество всех первообразных; б) первообразную, график которой проходит через точку А( 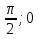 ) )3. Вычислите: а) 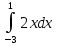 ; ;б) 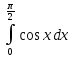 . .4. Вычислите площадь фигуры, ограниченной линиями у= 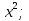 х=1; х=3; х=0 Дополнительная часть. х=1; х=3; х=0 Дополнительная часть.6. Вычислите площадь фигуры, ограниченной графиком функции у=8х-2 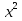 , касательной к этой параболе в ее вершине, и прямой х=0 , касательной к этой параболе в ее вершине, и прямой х=07. Вычислите: а) 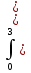 Зх+1) 3dx; б) Зх+1) 3dx; б)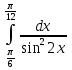 . .Критерий оценок
ИПМ 11. Дифференцированное домашнее задание . Цели: - формирование интереса к математике; - развитие математических способностей, расширение математическо - го кругозора; - развитие навыков работы с дополнительной к справочной литерату - рой; - выявление творческих умений учащихся, Сущность: - детям для домашней работы даются задания, содержащие: а) обязательный программный материал; б) задания более высокого уровня сложности, помечаемые учителем "зведочкой" (*). Автор использует также практику индивидуальных домашних заданий, Сущность: - отдельным учащимся предлагается выполнить дома определен ную работу с целью дальнейшего рассмотрения ее на уроке, Пример: задачи по теме « Применение интеграла » . ИПМ 12. Урок математики в разноуровневом классе. Специфика разноуровневого класса: в одном классе собраны дети с различными (часто диаметрально противоположными) уровнями восприятия учебного материала, Помимо традиционных учебных задач (проверка знаний, формирование новых понятий, установление закономерностей, алгоритмов, закрепление изученного материала) на уроке ставлю перед собой задачи:
Выполнение этих задач достигается с помощью:
(см. ИПМ 12.1( Приложение));
-дифференцированных самостоятельных и контрольных работ (см. ИПМ7-10). ИПМ 12.1. Фрагмент урока алгебры в 9 классе.(Приложение). Содержит элементы программированного обучения. Сущность: - подача материала небольшими информационными блоками;
Тема урока: « Неравенства 2-ой степени » Цели: - сформировать у учащихся понятие «Неравенство второй степени»; -добиться усвоения каждым учеником этого понятия; -формирование логического мышления, умения рассуждать. Неравенства второй степени Неравенство видя ах2 + bх+с > 0, или ах2 +bх+с<0, где а 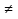 0, 0,называется неравенством второй степени или квадратным неравенством. Примеры квадратных неравенств: Зх2+5х I 7>0, Зх + 7-4х2 <0, 15х2-1>0, х2-4х<0, х2 <0. Вопрос учителя: 1. Является ли неравенство 7х2 - х - 9 > 0 1. Да квадратным? 2. Можно ли неравенство вида 9х2 - 15х+7 > 6х назвать квадратным ? В случае ответа "да" — вопрос "почему". Если ответ отсутствует, то: 2а. Пользуясь одним из свойств неравенств, перенесите 6х в левую часть. 2б. Получите неравенство 9х2-21х+7>0. 2в. Да. Работа по закреплению понятия — 5 мин. 1. Работа с классом. Задание. Выбрать среди неравенств квадратичные: 3х + 5х2 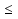 0; 4-х<0; 2 + х2 >0; 4х + 5 0; 4-х<0; 2 + х2 >0; 4х + 5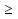 0; 13х~6<3х2; 0; 13х~6<3х2;14х2<0; -7>Зх2+11; Зх2-4х + 5<12г + Зх2+4. Приведите примеры квадратных неравенств. 2. Индивидуальная работа учащихся по карточкам. Содержание карточек. Выбрать среди неравенств квадратичные: 21х + х2>0; 7х-3<21х2; 78х2>1; х<14; 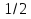 х + 4<0; Зх2 > 0: Зх2 -4х <5х2; х + 4<0; Зх2 > 0: Зх2 -4х <5х2;4 + 5х-13х2 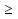 4 + 13х2; 5-2х2 4 + 13х2; 5-2х2 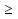 0. 0.Учитель собирает карточки, просматривая сразу правильность выполнения работы. В случае неверных ответов часть их выписывается на доску и предлагается учащимся всего класса их исправить. ИПМ 12.2. Урок математики в 5 классе, (Приложение). Тема: "Признаки делимости". Цели - закрепить у учащихся знание признаков делимости:
Для индивидуализации обучения на уроке используются карточки, дифференцированная самостоятельная работа. Ход урока, Опрос учащихся; (индивидуальная работа по карточкам и фронтальный опрос). Карточки: К-1. Определите, какие из чисел делятся на 4, проверьте свой вывод делением. Укажите число делящееся одновременно па 2 и 3. 164; 230; 1124; 2080; 2118; К-2. Определите, какие из данных чисел делятся на 25, проверьте свой вывод делением. Укажите одно из данных чисел, делящееся одно временно на 9 и 3. 125; 7536; 2700; 2510; 375; Материал для фронтального опроса: (метод поиска правильного ответа). Какие из чисел делятся на ... 1 2 3 912 520 173 па 10; на 3; 234 150 104 на 5; на 9; 120 175 701 на 2; на 5; 762 540 975 на 2: на 10; 153 149 307 на 9; 503 750 432 на 25; на 4; Примечание: в работе учащиеся используют таблички с номерами 1; 2; 3 для обозначения ответа. Во время устной работы учащиеся говорят признаки делимости на 2. 5, 3, 9,25,4, 10 Вывод (учащиеся заканчивают произносимую учителем фразу): 1. Чтобы решить, делится ли данное число на 2, 5, 10, 4, 25 нужно смотреть на... последнюю цифру в записи числа или две последних цифры. 2. Чтобы решить, делится ли данное число на 3 или 9 нужно.,, найти сумму цифр в записи этого числя. Затем вместе с учащимися слушаем ответы рабо тавших у доски школьников, Далее учащимся предлагается выполнить задание; № 1 (письменно) на магнитную десну крепится таблица с числами: 187; 723; 5652; 918; 8025; 7776; 405; 835; 1506; 711. Выписать в стройку числа, которые: а) делятся на 3; б) делятся на 9; в) на 2 и 3 одновременно; г) на 3 и 5 одновременно. Устное задание (крепится таблица на магнитную доску). Не выполняя действий, определите, делится ли на 5 а) 416-300 6)151-37 В)410 + 755 г)215+ 113 д)ЗЗ3 - 28 е) 225 - 85 Во время ответов спрашивать свойства делимости. № 2 (письменно) замените * в записи 4-хзначного числа такой цифрой, чтобы число делилось на 2, 3, 5, 9, 10. Рассмотрите все возможные случаи. 273*. Проверочная самостоятельная работа Обязательная часть (учебник стр. 103) I вариант П вариант № 336 (в, д) № 336 (б, г) № 339 (а) № 339 (б) Дополнительная часть 1. Учебник №341 №342 2. Дидактический материал стр.3 б №13 (1а) №13(16] В конце урока взять тетради на проверку, Домашнее задание: дидактический материал стр.36 № № 8, 11, 12(2,3,4). ИПМ 12.3. Фрагмент урока геометрии в 8 классе.(Приложение). На уроке используются элементы проблемного обучения, индивидуальная работа по карточкам, в конце урока проводится обучающая самостоятельная работа по многовариантным дидактическим материалам, разработанным автором опыта. |