Забельникова Ольга Васильевна. Место работы и должность: мбоу-сош №4 города Тулы, учитель математики. Образование: высшее, тгпи им. Л. Н. Толстого, 1982г., диплом
 Скачать 464.62 Kb. Скачать 464.62 Kb.
|
| Тема урока: «Теорема Пифагора». Цели урока: - пробудить у учащихся интерес к сознательному усвоению теоремы Пифагора. -добиться сознательного усвоения теоремы;
Ход урока.. 1.Организационный момент. Проверка домашнего задания не осуществляется, т.к. на предыдущем уроке проводилась контрольная работа. 2.Устная работа. Цель: активизация опорных знаний учащихся.
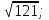 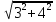 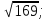 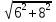 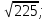 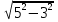 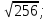 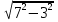 2) Решите уравнения: х2=4; х2=7. 3) Вспомните, как называются элементы прямоугольного треугольника и определение косинуса острого угла прямоугольного треугольника. 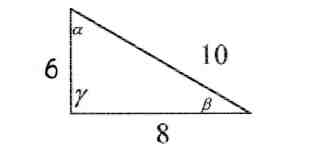 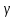 = 90° = 90°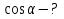 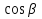 -? -?3. Объяснение нового материала. ПРОБЛЕМА. Необходимо сделать лестницу так, чтобы один её конец находился на расстоянии 4м от стены дома, а другой конец -на стыке стены и крыши. Какова должна быть длина лестницы? (Дети представляют ситуацию, говорят, что из себя будет представлять конструкция, делают совместно с учителем чертёж). 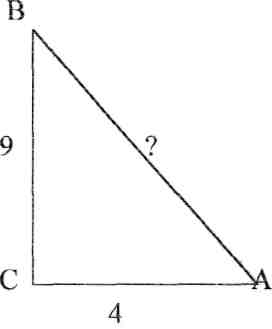 Учитель: решить задачу пока не можем. Помочь в решении нашей проблемы может теорема, названная в честь великого греческого ученого Пифагора. (Далее заслушиваются сообщения 2-3 учеников о Пифагоре) Учитель:В современных учебниках теорема Пифагора формулируется так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Научная формулировки: «Если длины сторон прямоугольного треугольника измеряются в одних и тех же единицах, то квадрат длины гипотенузы равен сумме длин квадратов катетов». Изобразим прямоугольный треугольник АВС с прямым углом С и запишем формулировку в обозначениях: 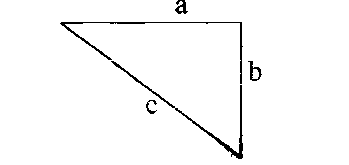 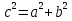 Во времена Пифагора теорема звучала так: «Квадрат, построенный на гипотенузе треугольника, равен сумме квадратов, построенных на его катетах.» Из сообщений ребят мы уже знаем, что эта теорема имеет богатую историю. В настоящее время известно более 100 доказательств теоремы Пифагора. Итак, докажем теорему Пифагора (ещё раз сформулировать теорему при помощи детей). Теорема доказывается совместно с учащимися с помощью наводяших вопросов учителя. ……………………………………………………………………………… 4. Закрепление нового материала. 6 школьников работают по карточкам 2-х видов на местах, остальные учащиеся решают задачи по готовым чертежам Задача 1 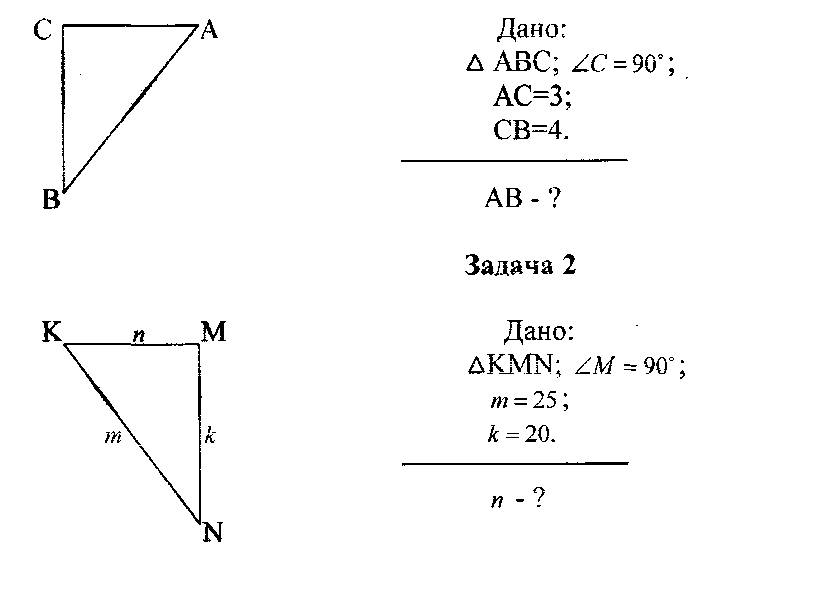 КАРТОЧКА 1 1) В прямоугольном треугольнике АВС Варианты ответа С = 90°; 1.136 с = 10; а = 6, 2. 8 Найти b-? 3. 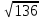 2) В прямоугольном треугольнике МКР Варианты ответа М = 90° 1.5 п = 1; p = 2. 2. 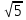 Найти m-? 3. 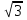 КАРТОЧКА 2, 1) В прямоугольном треугольнике АВС Варианты ответа С = 90°; 1.16 с = 20; а = 12. 2. 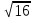 Найти b -? 3 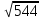 2) В прямоугольном треугольнике РКМ Варианты ответа K=90°; 1.28 n = 8; р = 6. 2, 10 Найти k-? 3. 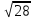 В конце урока (за 15-20 мин. до окончания) проводится многовариантная обучающая самостоятельная работа (см. ИПМ 9.2.(Приложение)). ИПМ 13.Индивидуальная учебная работа с учащимися во внеурочное время. Цели; - пробуждение и развитие интереса учащихся к математике;
Содержание индивидуальной работы:
Виды индивидуальной работы осуществляемые автором опыта:
1. Подготовка к поступлению в профильные классы, Форма работы - групповые консультации с учащимися. Сущность- - учащимся предлагаются подборки заданий по различным темам для решения дома; - через 1-2 недели задания обсуждаются на дополнительных заня тиях, рассматриваются различные варианты решения заданий, 2. Коррекция знаний учащихся. Форма работы - групповые и индивидуальные консультации, Сущность: - коррекция знаний учащихся по определенным разделам учебно го материала при помощи максимальной индивидуализации обучения в однородных, с точки зрения способности к обучае мости, группах. Технология: - учащиеся организуются в группы по 4-5 человек, затем автор опыта проводит с ними работу по схеме: повторное решение запоминание самостоятельная изложение примеров учащимися работа учащихся учителем учителем алгоритма по выполнению учебного выполнения заданий по материала заданий данного алгоритму типа ИПМ 13.1 Тематические карточки-задания для 7 класса (Приложение) КАРТОЧКА 1 1. Разложите на множители: 5х2-45 а 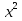 -4 а 18с-2р2с -4 а 18с-2р2сb 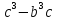 2. Представьте в виде произведения: 5а2+10ав+5в2 -2х2-8х-8 а 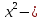 2аху+а 2аху+а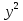 2х3+12х2-3х 2х3+12х2-3х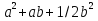 у4-8у+16 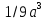 -3 -3-с+ 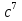 (с+5)с2-(с+5)2с+(с+5) 8а -в +4а +2ав+в 3. Разложите на множители: Зх+х 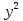 - -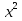 у-Зу у-Зу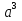 -аb- -аb-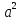 b+ b+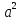 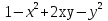 2х2-20ху+50у2-2 a 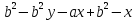 (х2+у)3-4х2у2(х2+у2) 4. Решите уравнение: 10х2+5х=0 25-100х2=0 Зх2-27=0 КАРТОЧКА 2 Задачи на проценты
ИПМ 13.2. Карточки коррекции знаний учащихся.(Приложение). КАРТОЧКА I Тема: «Неравенства 2-ой степени с одной переменной» (9 класс). 1). Для параболы у = 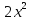 - х -15 - х -15а) определите направление ветвей; б) найдите абсциссы точек пересечения параболы с осью х, решив уравнение 2х2 - х -15 = 0; в) изобразите схематично график: г) найдите по графику значения х, при которых у > 0 и при которых у >0. 2). Решите неравенство Зх2+11х-4< КАРТОЧКА 2 Тема: «Интеграл » (11 класс). 1). Для функции f(х) = х5 а) найдите общий вид первообразных F(x) б) найдите F(2) и F(0) в) вычислите Р(2)-Р(0). 2). 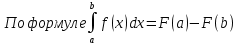 вычислите: вычислите:а) 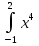 dx; dx; 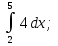 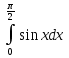 . .3). Вычислите площадь заштрихованной фигуры: 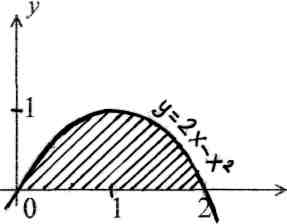 x xИПМ 14.Творческие работы учащихся, Цели: - Формирование интереса к предмету; - развитие умения работать с научно-популярной литературой; -расширение представлений учащихся о практическом значении математики. Автор предлагает учащимся в процессе обучения выполнять творческие задания по различным темам. Это могут быть: доклады и сообщения учащихся на уроках о жизни и творчестве известных математиков; выполнение рисунков, эскизов; изготовление моделей. Примеры: - доклады: «Пифагор»: «Теорема Пифагора»: «Герон»: «Фалес Милетский» и т.д.;
ИПМ 15. Подготовка и проведение внеклассных мероприятий как форма индивидуальной работы с учащимися. Автор опыта считает внеклассные мероприятия самыми демократичными в плане реализации индивидуальности каждого ребенка. цели: - развитие устойчивого интереса к математике;
Сущность: за основу берутся популярные молодежные передачи и формы их проведения, затем "привязываются" к математике. Свою задачу вижу в том, чтобы в подготовке и проведении мероприятия приняли участие все учащиеся. Возможные формы участия школьников в мероприятии:
ИПМ 15.1 Разработка внеклассного мероприятия для 5-6 класса "Знатоки математики " (Приложение) В конкурсе участвует 4 команды по о человек (от каждою класса) или класс разбивается на 4 команды. Учащиеся, не вошедшие в состав команды, участвуют в конкурсе в качестве болельщиков. Подготовительная работа: за 3-4 дня до начала конкурса команды готовят: 1) название; 2) эмблемы; 3) приветствие (2 мин). Оборудование: 4 стола по 6 стульев за каждым столом, экран с названием команд, конверты с квадратами 2-х цветов (красные и зеленые), 1 стол для жюри, гонг. Замечание:Для ведения конкурса целесообразно выделить 2-х или 3-х учащихся, не участвующих в игре, для работы с экраном соревнования. Система оценки: правильный ответ - красный квадратик, в случае неправильного ответа команда болельщиков помогает команде: если ответ болельщиков верен, команда получает зеленый квадрат. Пет ответа - команда не получает квадратик. 2 зеленых квадрата равноценны одному красному. Полномочия жюри:
(В жюри "сильные" учащиеся во главе с учителем). Цель мероприятия:
Ход конкурса: I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ:
II. КОНКУРС "ЗНАТОКОВ МАТЕМАТИКИ".
Представитель каждой команды подходит к ведущему и вытягивает один из предлагаемых ему листов с заданием (подходят и вытаскивают задания все представители одновременно), затем по удару гонга все возвращают- ся в команды и в течении I мин. обсуждают задание, ответ записывают на листок Через минуту по удару гонга возвращаются, встают рядом с веду щим. оглашают свои ответы. Жюри оценивает конкурс (1 красный или зе леный з случае помощи болельщиков квадрат Задания ОРЬДБ - ДРОБЬ УЛГО - УГОЛ ИДЛАН - ДЛИНА РКГУ - КРУГ III. Аналогия: Этот тур проводится по той же схеме, что и II. Задания для команд: 1) Исключите лишнюю фигуру: 0 12 3 (0 - замкнутая ломаная; 1 - ломаная, состоящая из 2-х звеньев, остальные из 4-х). 2) Исключите лишнее слово: СУММА; РАЗНОСТЬ; МНОЖИТЕЛЬ; ЧАСТНОЕ. (множитель - компонент действия). 3) Подумайте, что объединяет слова в верхней строчке и отметьте в нижней слово, которое к ним подходит: ДЛИНА; ПЛОЩАДЬ; МАССА а) секунда; б) цен I нор; в) объем; г) метр 4) Подумав, как связаны два первых слова в верхнем ряду, в нижнем ряду укажите слово, которое связано с третьим: КВАДРАТ - ПРЯМОУГОЛЬНИК; КУБ -? а) шар: б) ромб, в) прямоугольный параллелепипед; г) пирамида 5) Поддайте, что объединяет фигуры верхнего ряда и выберите из нижнего ряда фигуру, которая к ним подходит:  2) Сколько а комнате кошек, если в каждом из 4-х углов сидит по кошке, претив каждой кошки по 3 кошки, на хвосте у каждой кошки по кошке? (4 кошки) 3) В корзине лежит 5 яблок. Как разделить эти яблоки между пятью девочками, чтобы каждая получила по одному яблоку и одно яблоко осталось в корзине? (Отдать корзину с яблоком) 4) В цехе вытачивают детали из заготовок. Из одной заготовки - 1 деталь. Из стружек, образовавшихся при выделке 6 деталей, можно изготовить еше одну заготовку. Сколько деталей можно сделать из 36 заготовок? (43) 5) В полдень из Москвы в Тулу выезжает автобус с пассажирами, часом позже из Тулы выезжает велосипедист и едет по тому же шоссе, но в 5 раз медленнее. Когда автобус и велосипедист встретятся, кто из них будет дальше от Москвы? (Одинаково) 6) Пользуясь только сложением, запишите число 28 при помощи пяти "двоек" (22+2+2+2) Подведение итогов конкурса. Во время подведения итогов ведущий задает вопросы "болельщикам". (Конкурс не оценивается - самый активный "болельщик" получает приз). 1. Два мальчика решали задачу 30 мин. Сколько минут решал задачу каждый мальчик? (30) 2. У кассы за помидорами стоят: 2 синих жирафа, 8 фиолетовых жирафят и 2 зеленых бегемота. Сколько животных стоит в очереди? (0 - таких не бывает) 3. Известный комментатор берется предсказать счет любого футбольного матча до того, как тот начнется. В чем секрет этих безошибочных предсказаний? (0:0) 4. Пастух (шагал) гнал гусей: один впереди 3-х идет; один 3-х подгоняет и 2 посередине идут. Сколько всего гусей? (4 штуки) 5. 5 лет назад разница лет брага и сестры равнялась 3. Чему она будет равна через 5 лет? (3 года ) 6. Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода? (Через 72 часа будет опять ночь и солнца не может быть) 6) Исключите лишнее слово: ДЕВЯТЬ; ДВЕНАДЦАТЬ: ВОСЕМЬ; ПЯТНАДЦАТЬ (восемь - не делится на 3) "Волшебный цветок" Ведущий держит "ромашку", на внутренней стороне каждого "лепестка" написана задача. Представители подходят, отрывают по "лепестку", по удару гонга садятся за столы; вместе с командой решают задачи, через 3 минуты по удару гонга с готовыми ответами (написаны на листок) подходят к ведущему, оглашают ответ. Жюри оценивает итоги конкурса Тексты задач. А) 1) Профессор ложится спать в 8 часов вечера и заводит будильник на 9 часов утра. Сколько часов спит профессор? (1 час) 2) Больному выписаны 3 укола- через полчаса каждый укол. Через какое время будут сделаны все уколы? (через 1 час) 3) Бревно распилили на 12 частей. Сколько было распилов? (11распилов) 4) У мальчика братьев нет, а у его сестры столько же братьев, сколько и сестер. Сколько в этой семье братьев и сестер'? (2 сестры и брат) 5) На лесопильном заводе машина отпиливает от бревна за 1 мин кусок в 1 метр. За сколько минут будет распилено бревно в 10 метров? (9 мин) Б) После подведения итогов этого этапа ведущий берег еще одну "ромашку" с более сложными задачами. Порядок проведения аналогичен. (Гонг через 4 мин). 1) В кругу расположены числа, из которых 2 множителя, а третье - их произведение. Найдите не менее 3-х таких "комплектов".  Примеры: (1  5=5; 2-2=4; 2 5=5; 2-2=4; 2 4=8; 1 4=8; 1 2 =2) 2 =2)- ЗАМЕЧАНИЕ: Если несколько команд будет иметь одинаковое количество баллов, предлагается конкурс: чья команда быстрее решит задачу
(Кладем 2 кольца: если весы в равновесии, то оставшееся кольцо легче; если одно перевесило - ответ ясен) На проведение конкурса требуется 45-55 минут. |