ПРИЛОЖЕНИЯ
1.Задание для подготовки к семинару
по теме: «Применение определенного интеграла к вычислению площадей фигур».
Вычислить площадь фигуры, ограниченной линиями:
1) 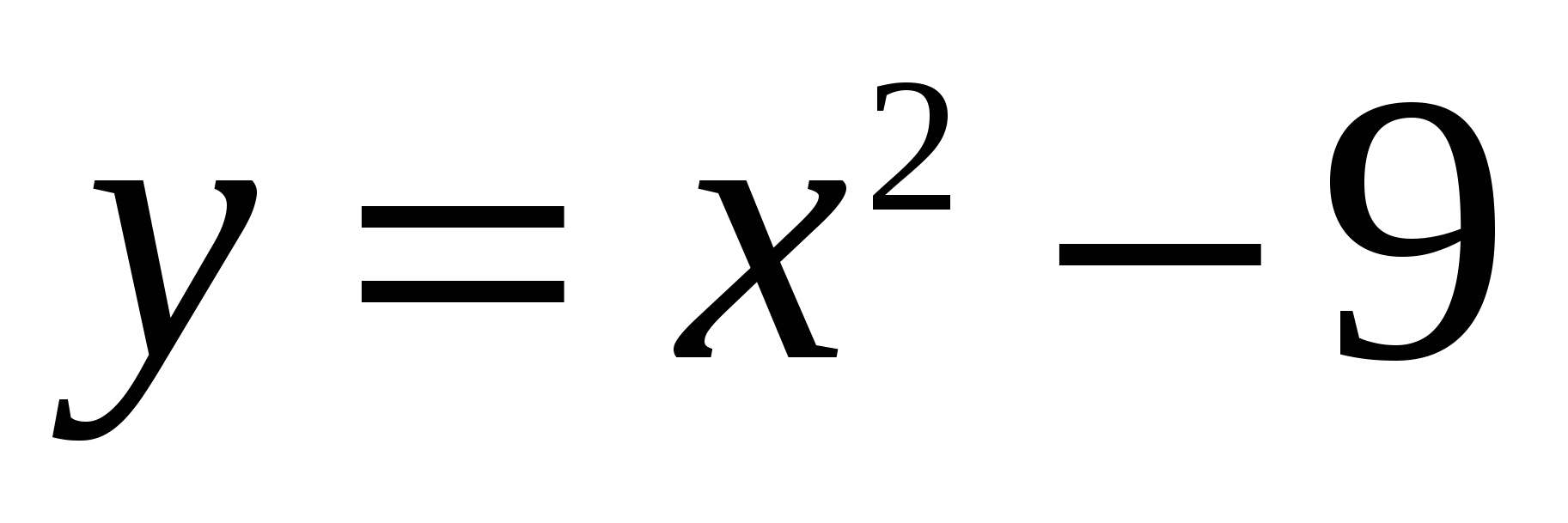 и и  ; ;
2) 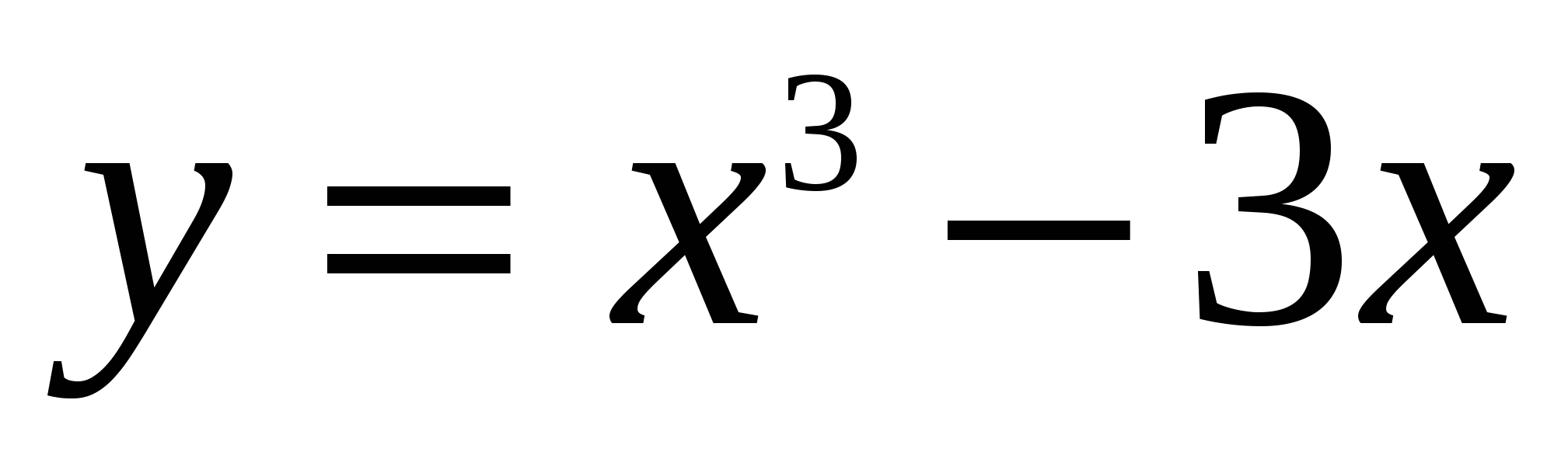 и осью абсцисс; и осью абсцисс;
3)  , ,  , , 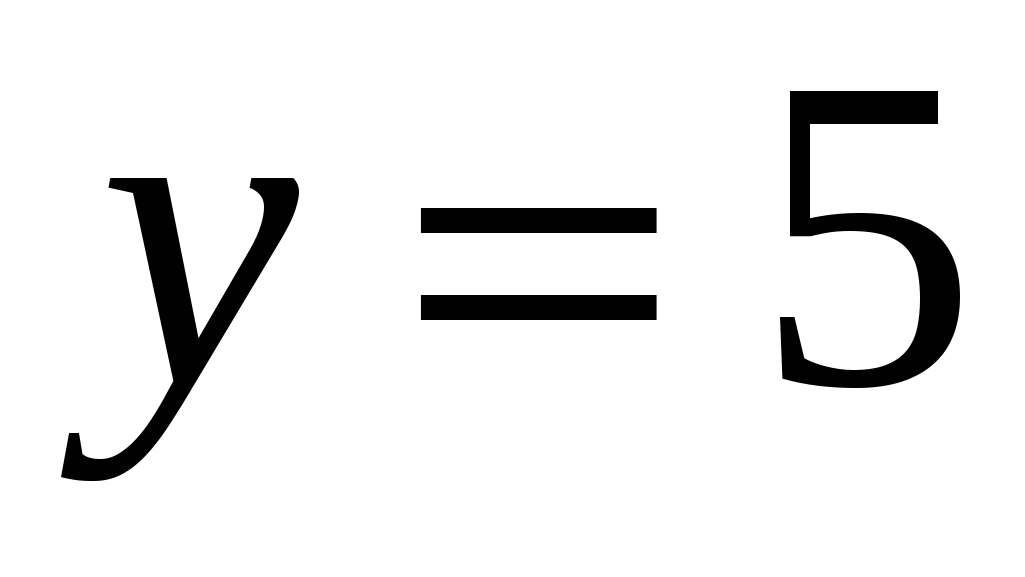 , , 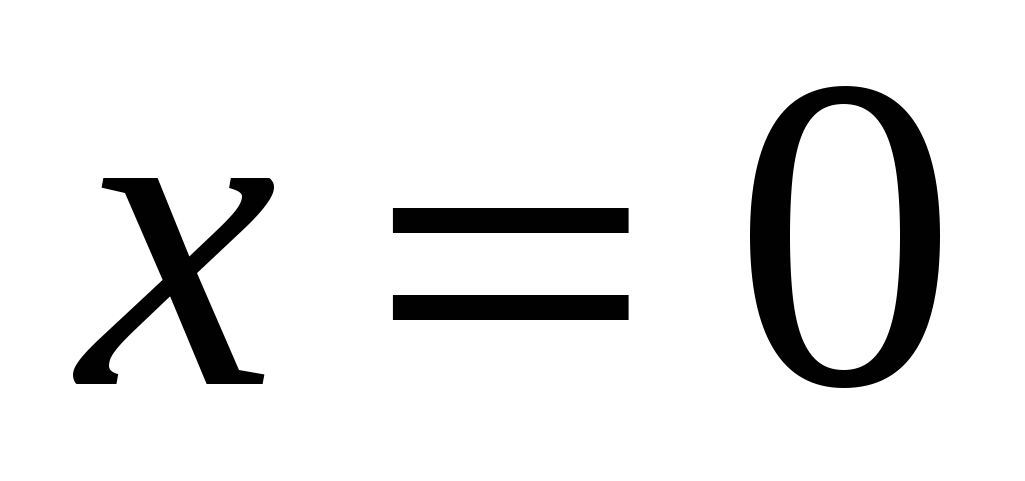 ; ;
4)  и осью абсцисс; и осью абсцисс;
5) 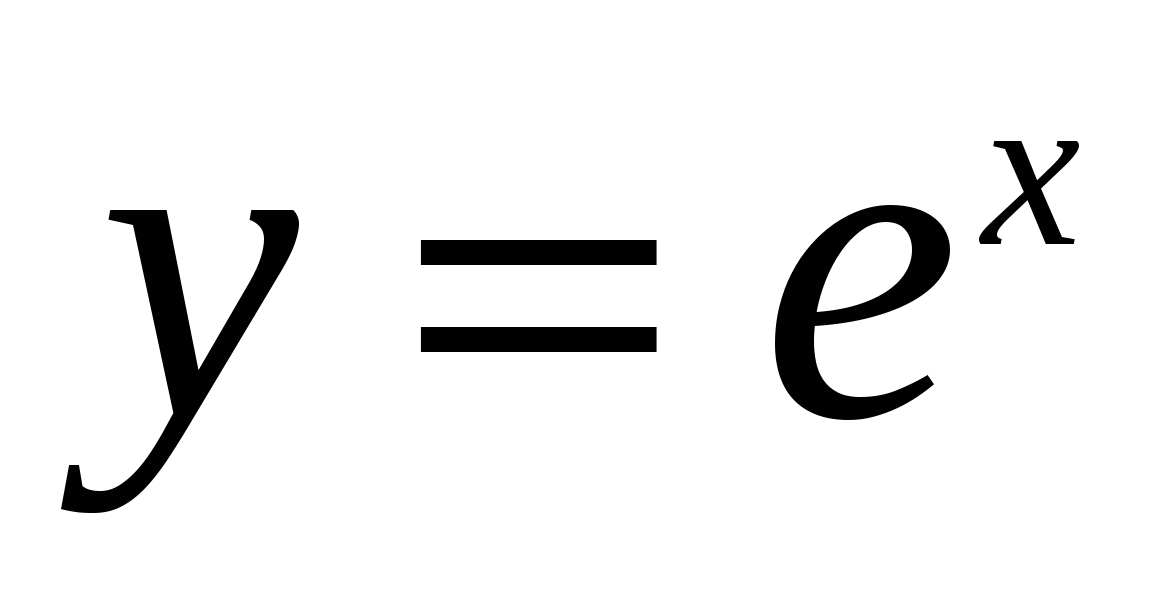 , ,  , , 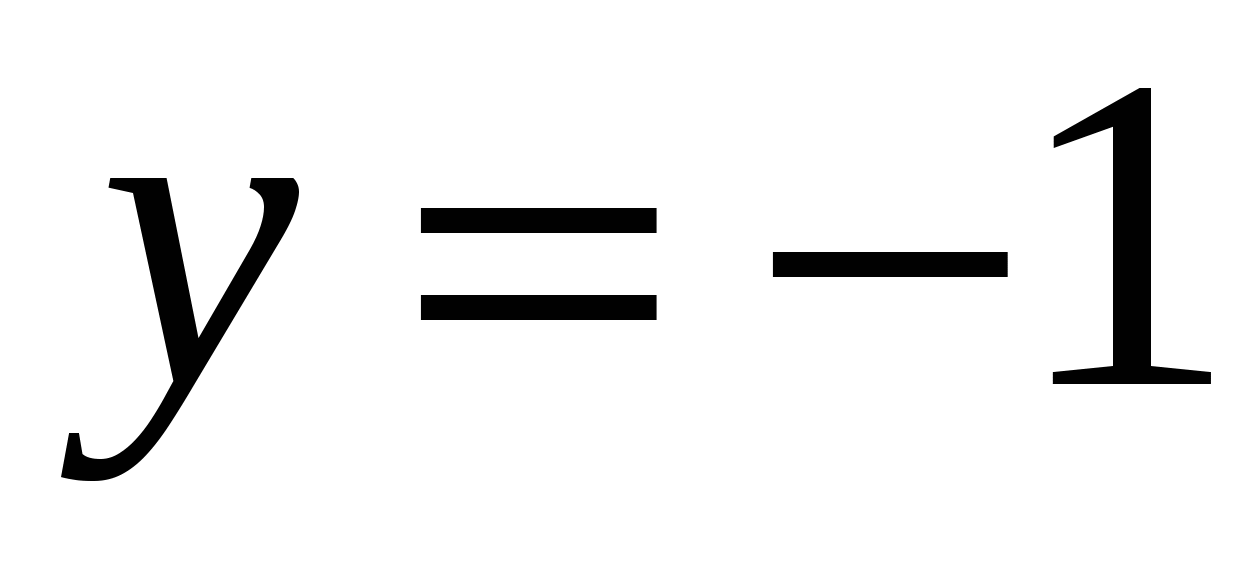 , , 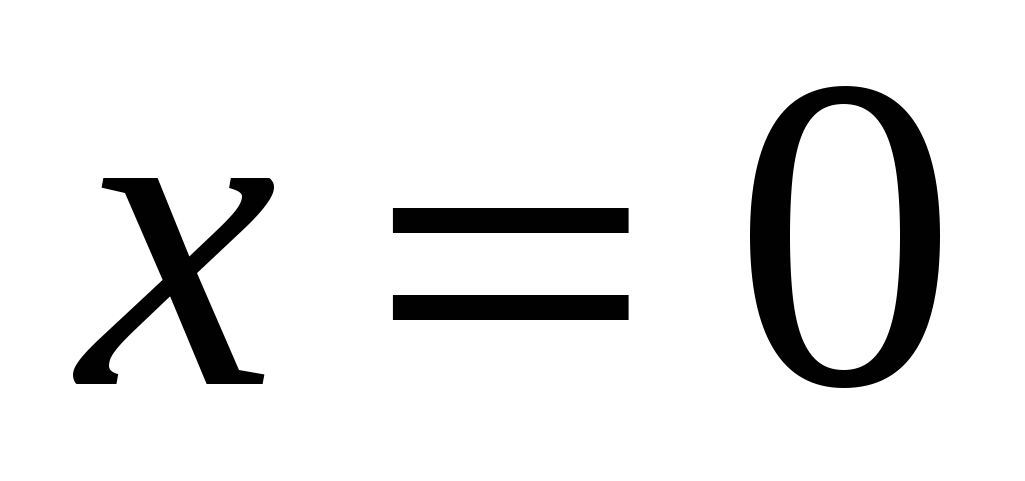 , , 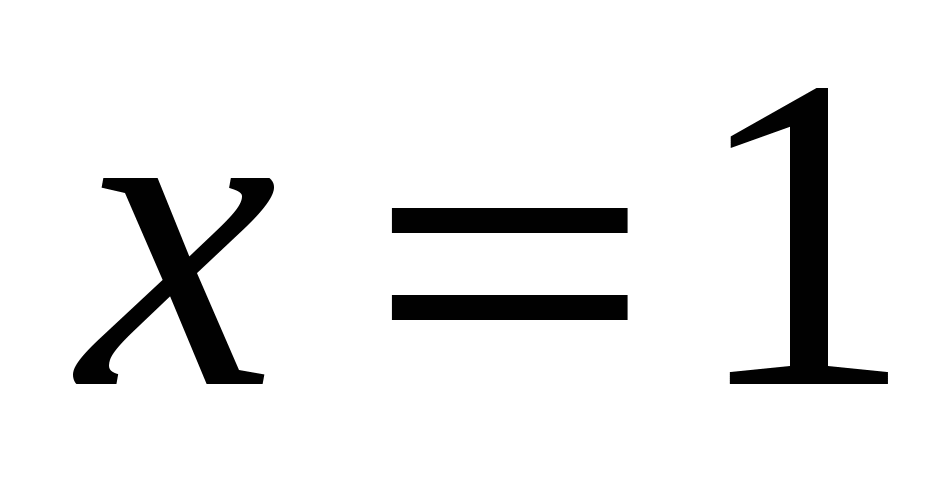 ; ;
6) 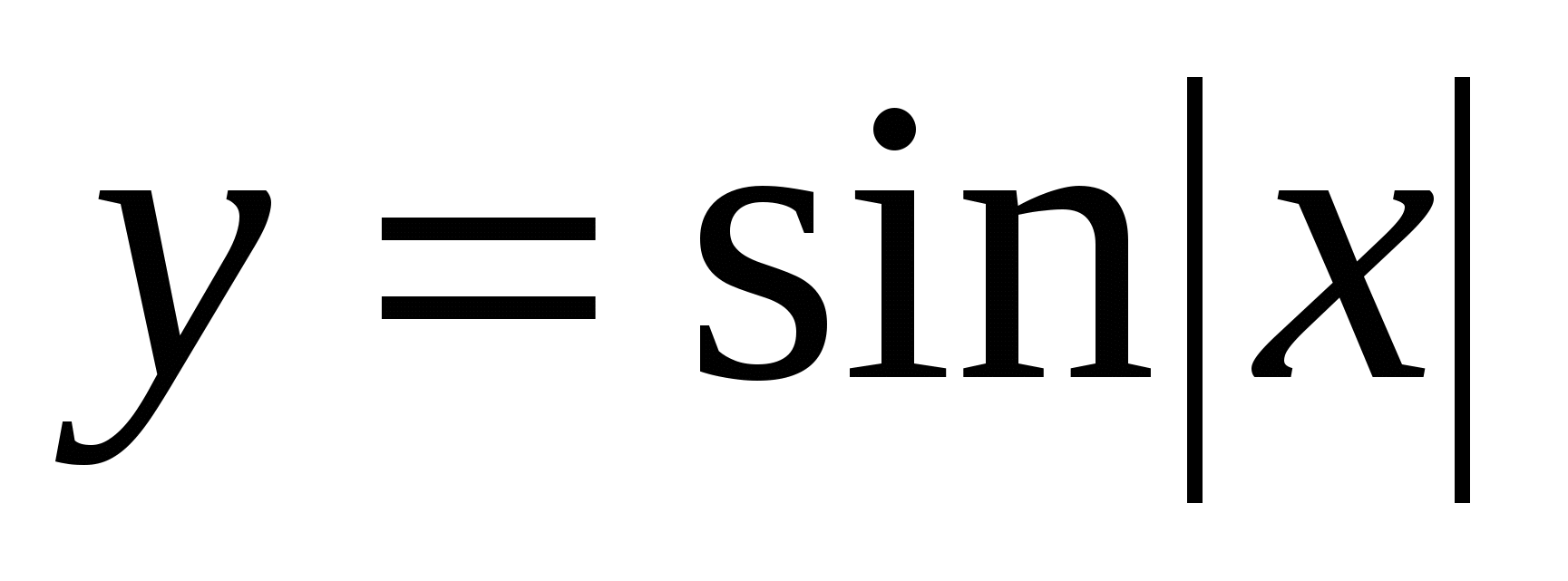 , , 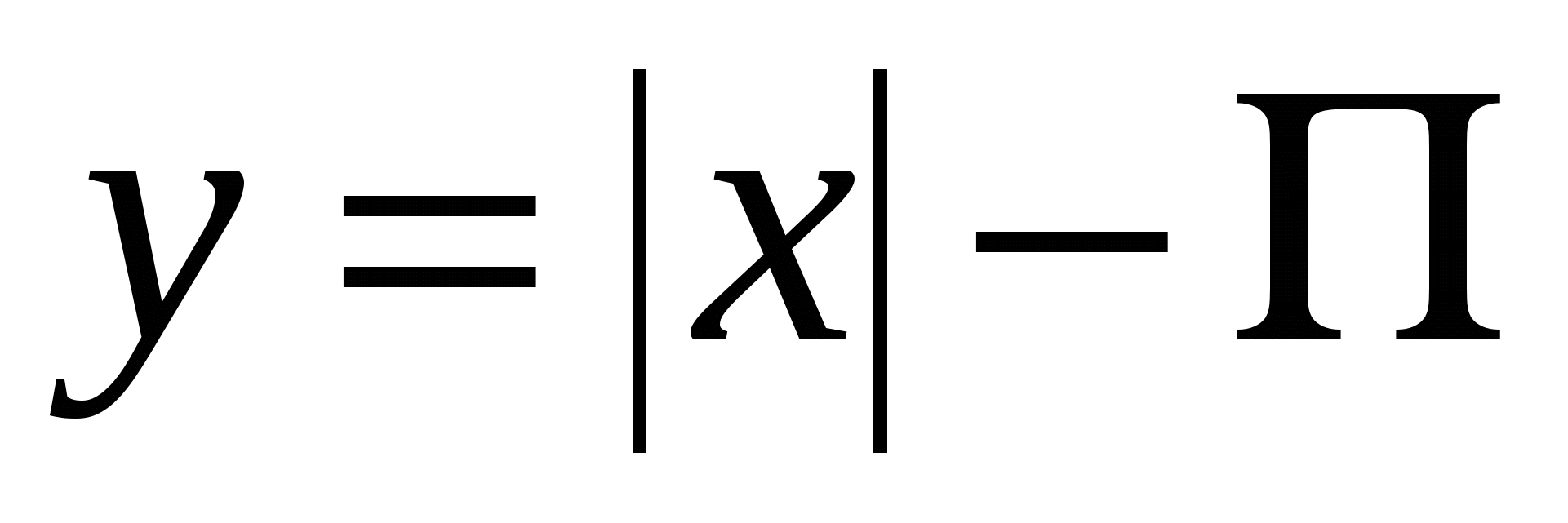 ; ;
7) 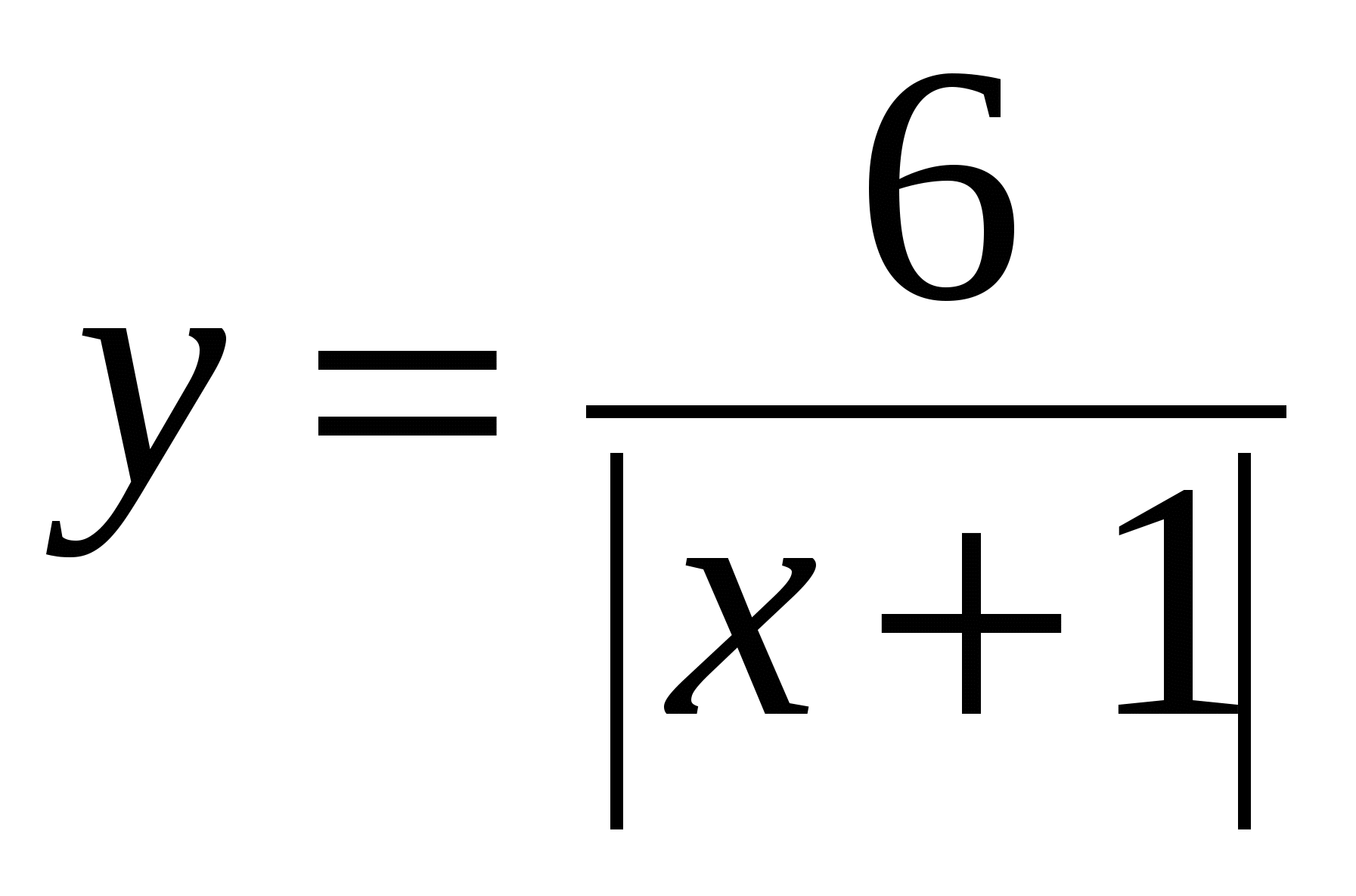 , , 
8)  , , 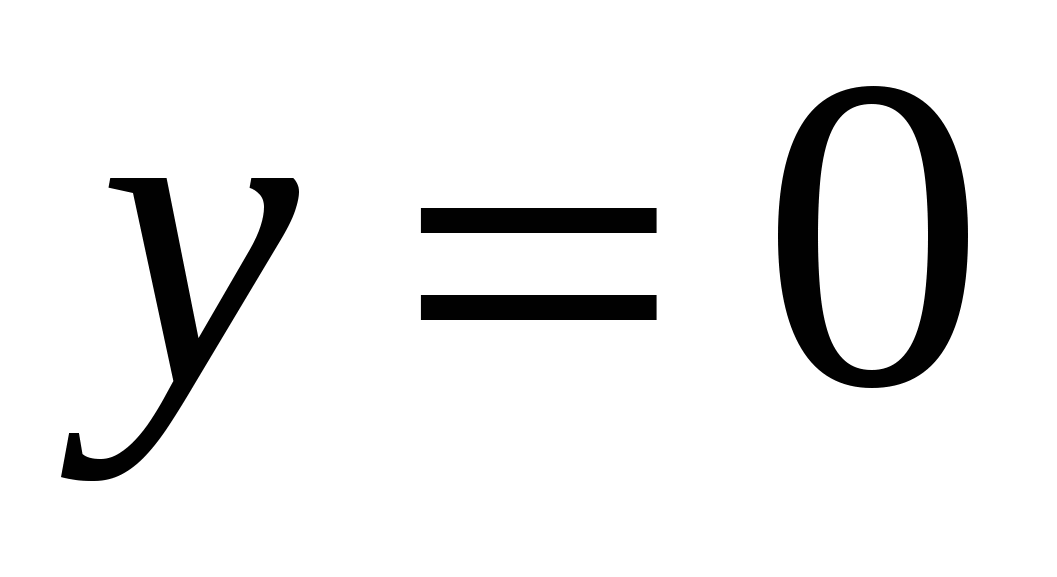 , , 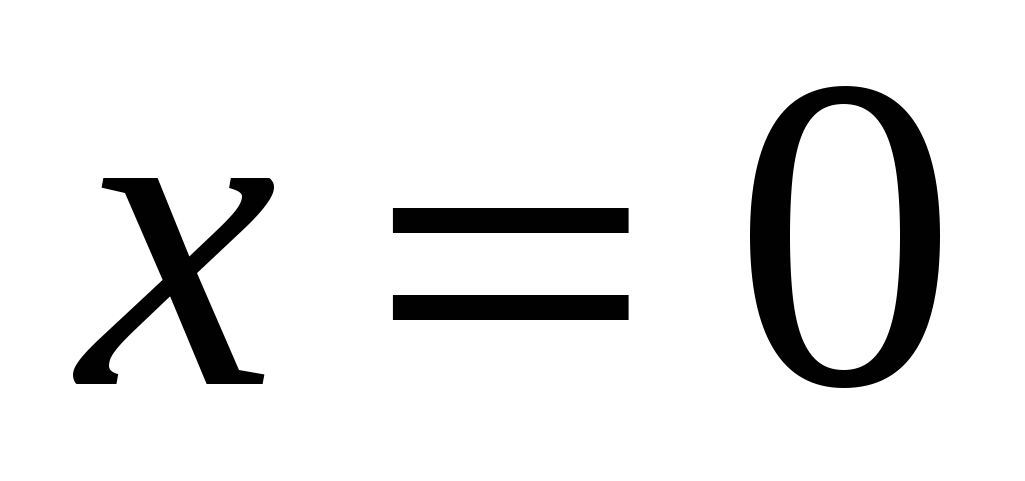 , , 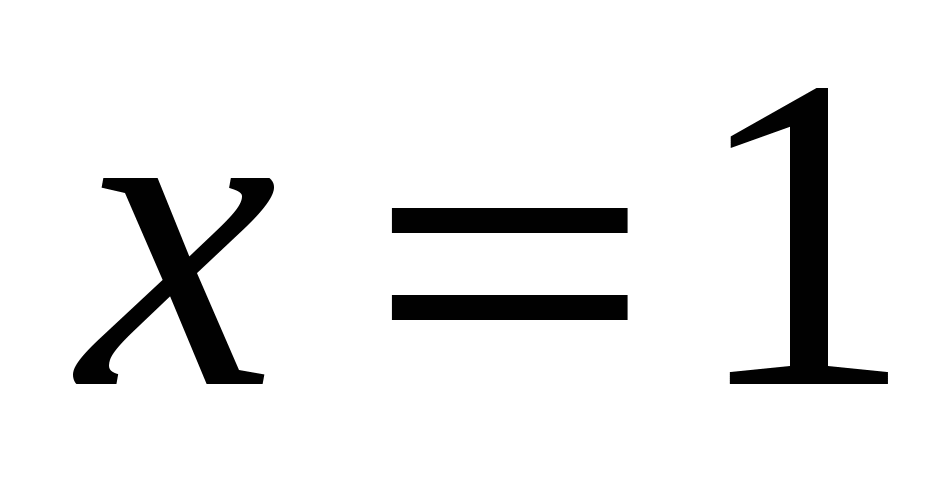 . .
Вычислите площадь фигуры, ограниченной графиком функции  и касательными к графику функции и касательными к графику функции  в точках в точках 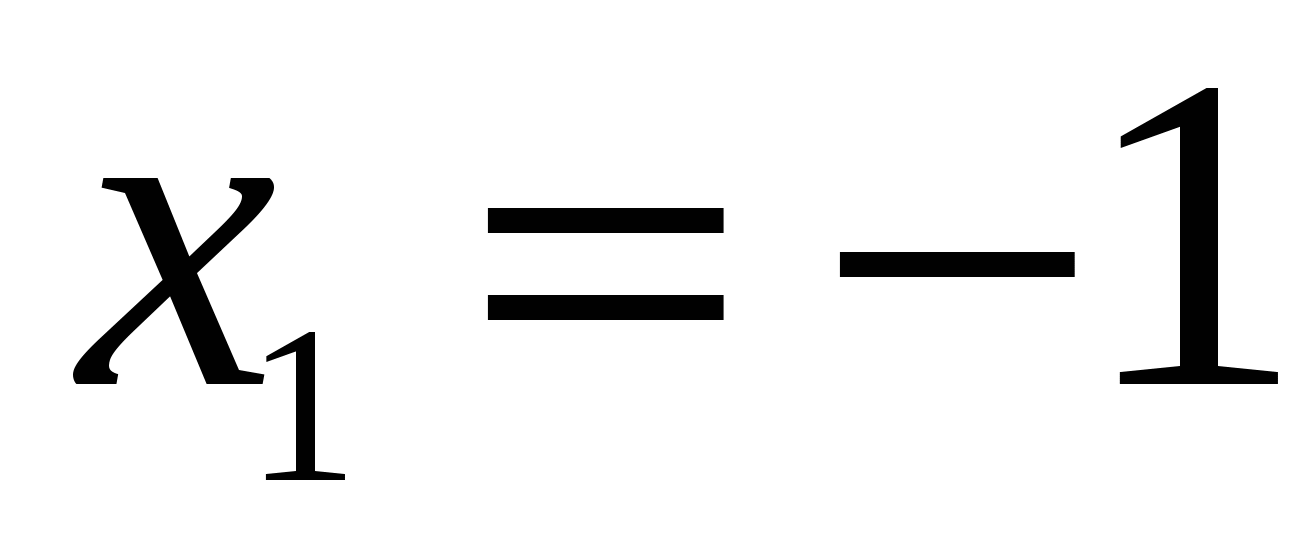 , , 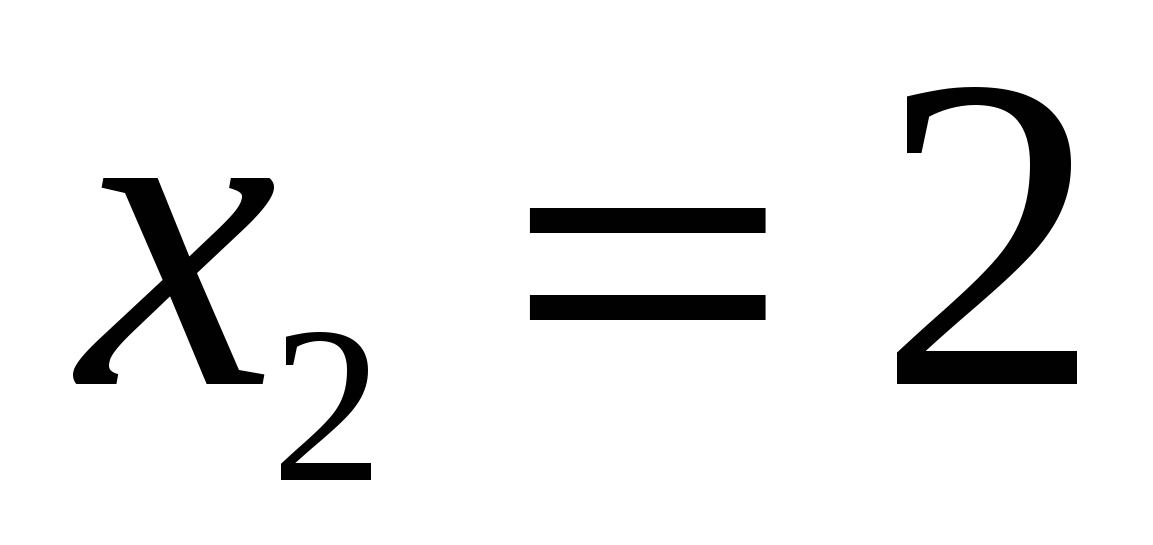 . .
Вычислите площадь фигуры, ограниченной линиями: 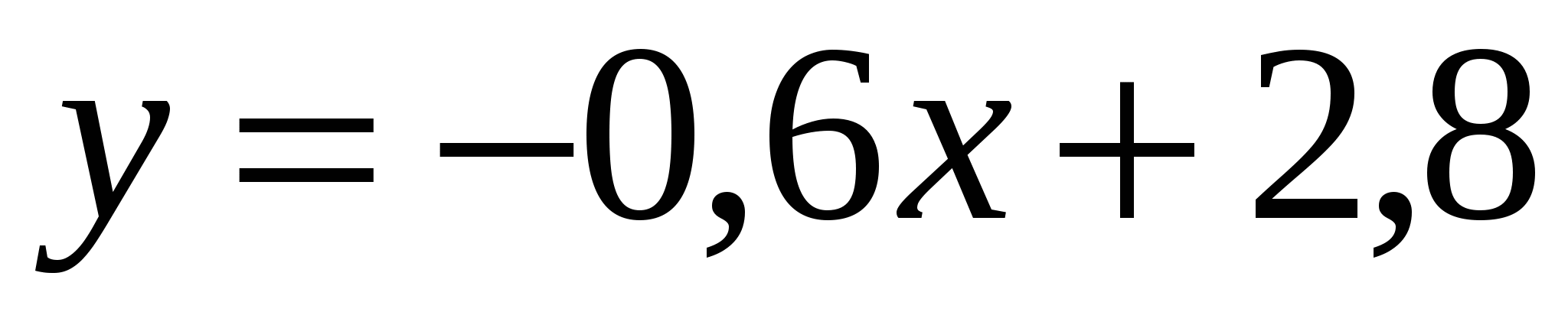 , , 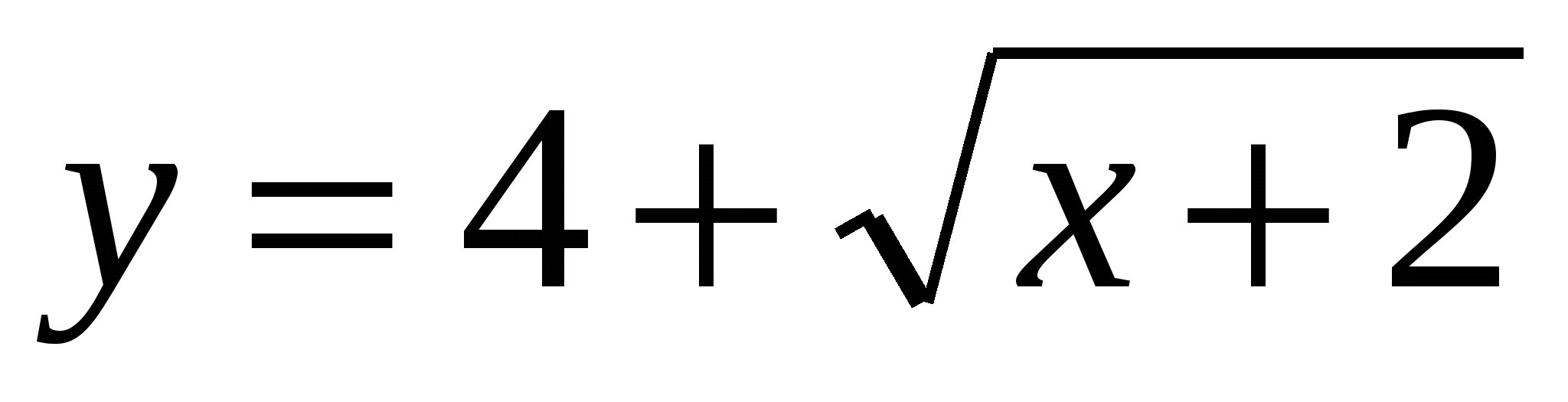 , , 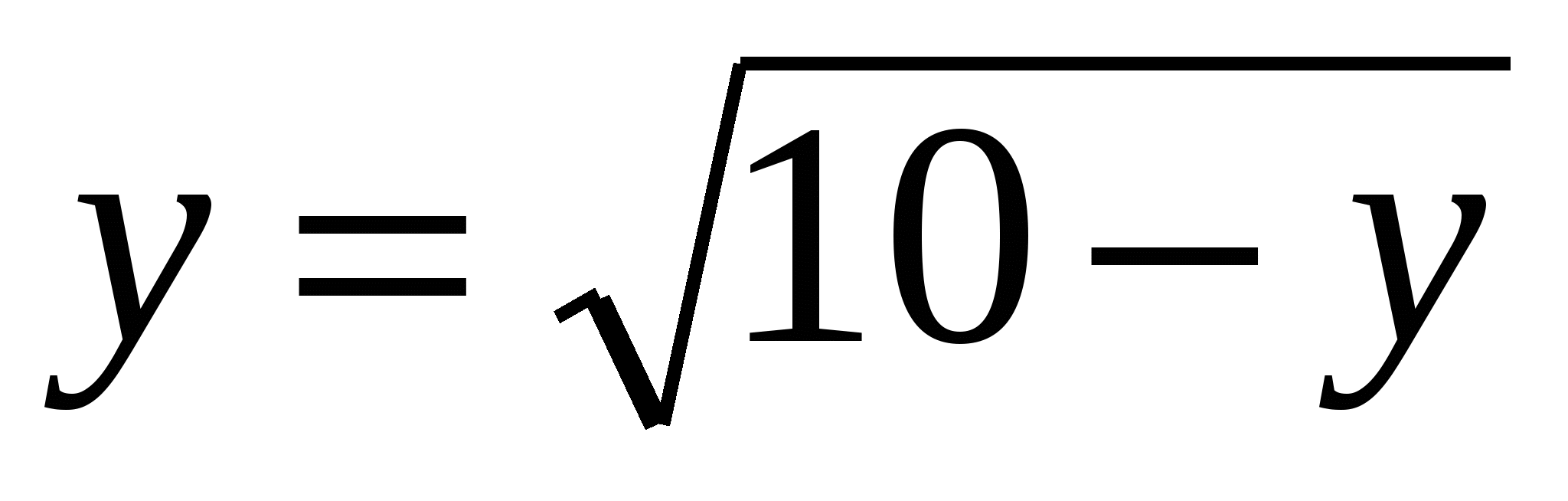 . .
Вычислите площадь фигуры, ограниченной линиями: 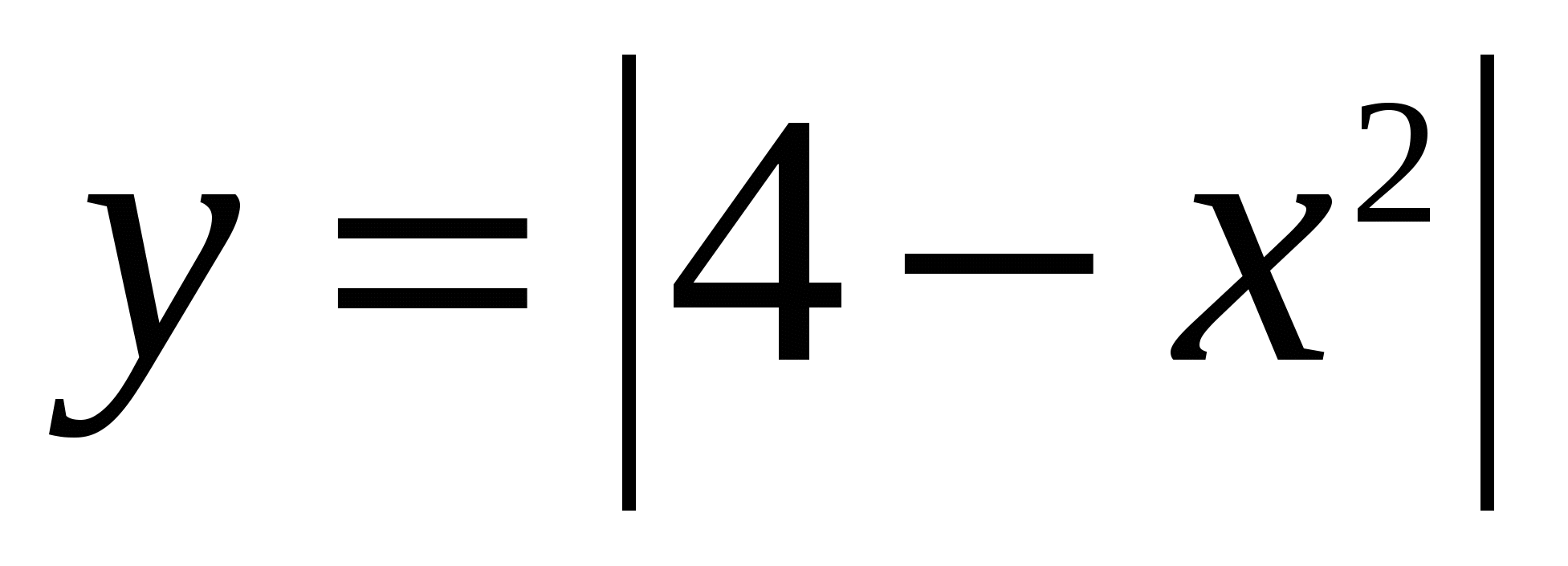 и и 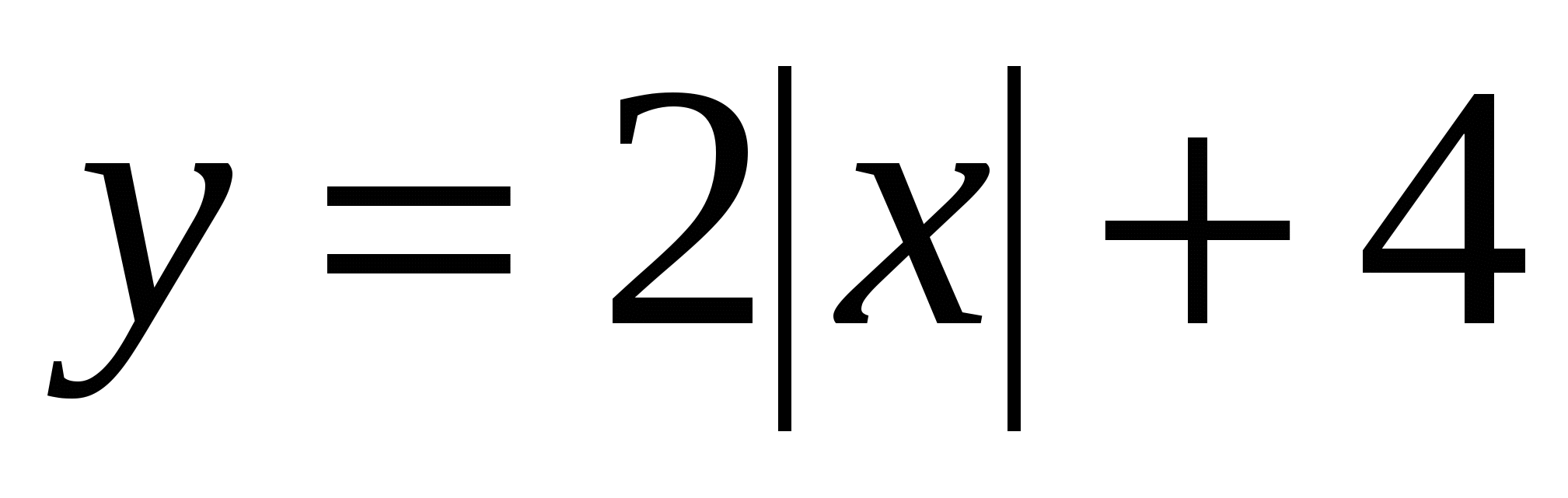 . .
Найдите площадь фигуры, ограниченной линиями: 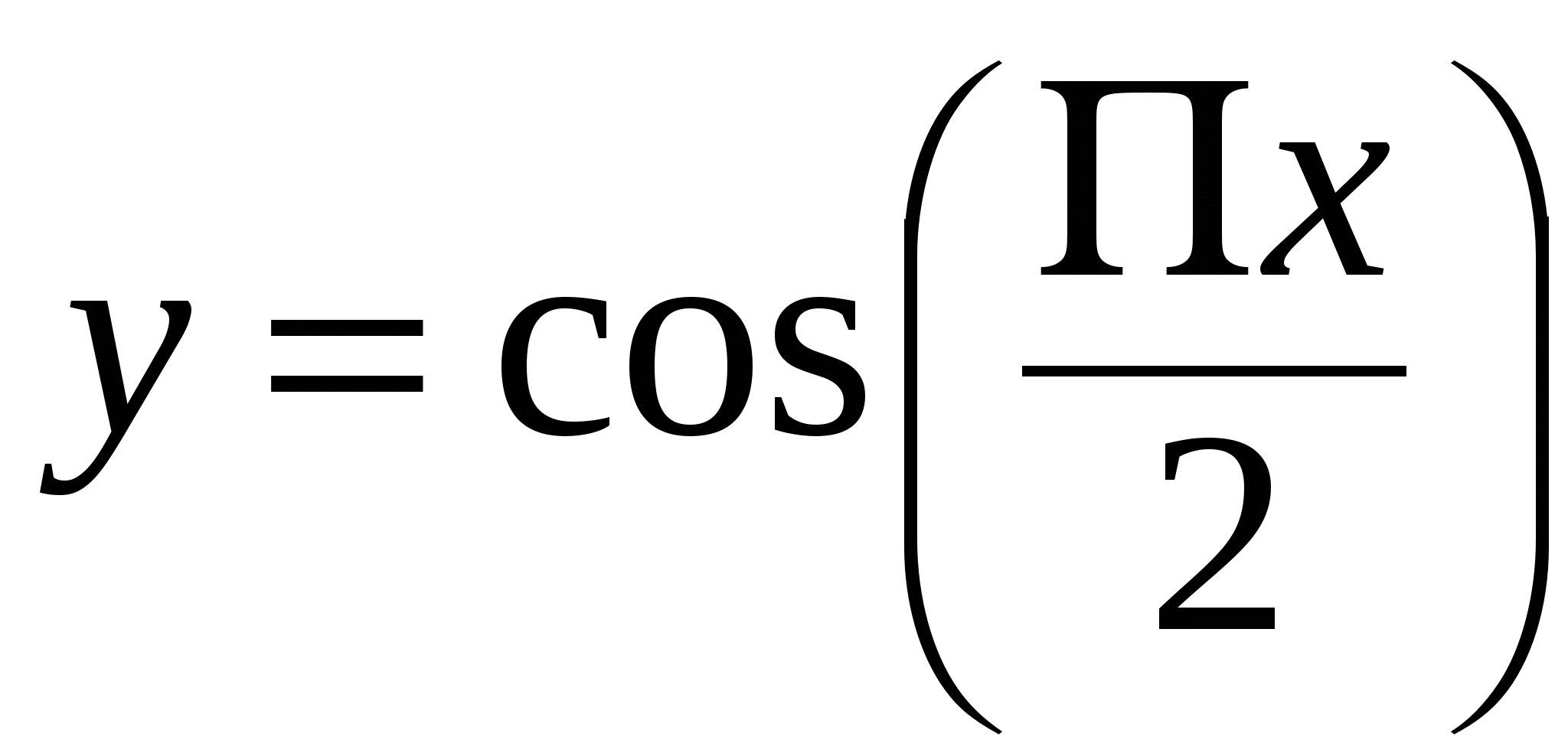 , , 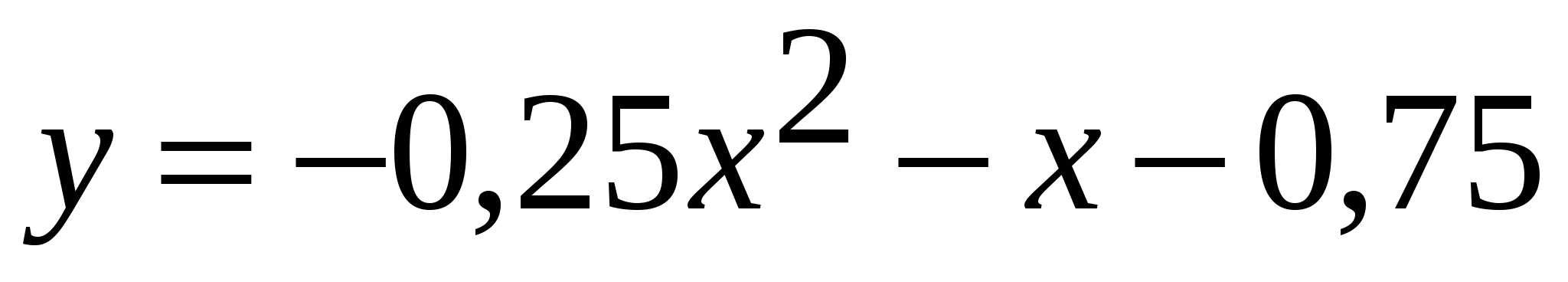 (абсциссы точек – целые числа). (абсциссы точек – целые числа).
2.План-задание
по теме: «Применение определенного интеграла к вычислению площадей фигур».
Краткое теоретическое обоснование применения определенного интеграла к вычислению площадей фигур. Некоторые примеры.
Использование симметрии фигур при вычислении их площадей.
Применение свойств взаимно обратных функций при вычислении площадей фигур.
3. Задание для практической работы.
Постройте линию 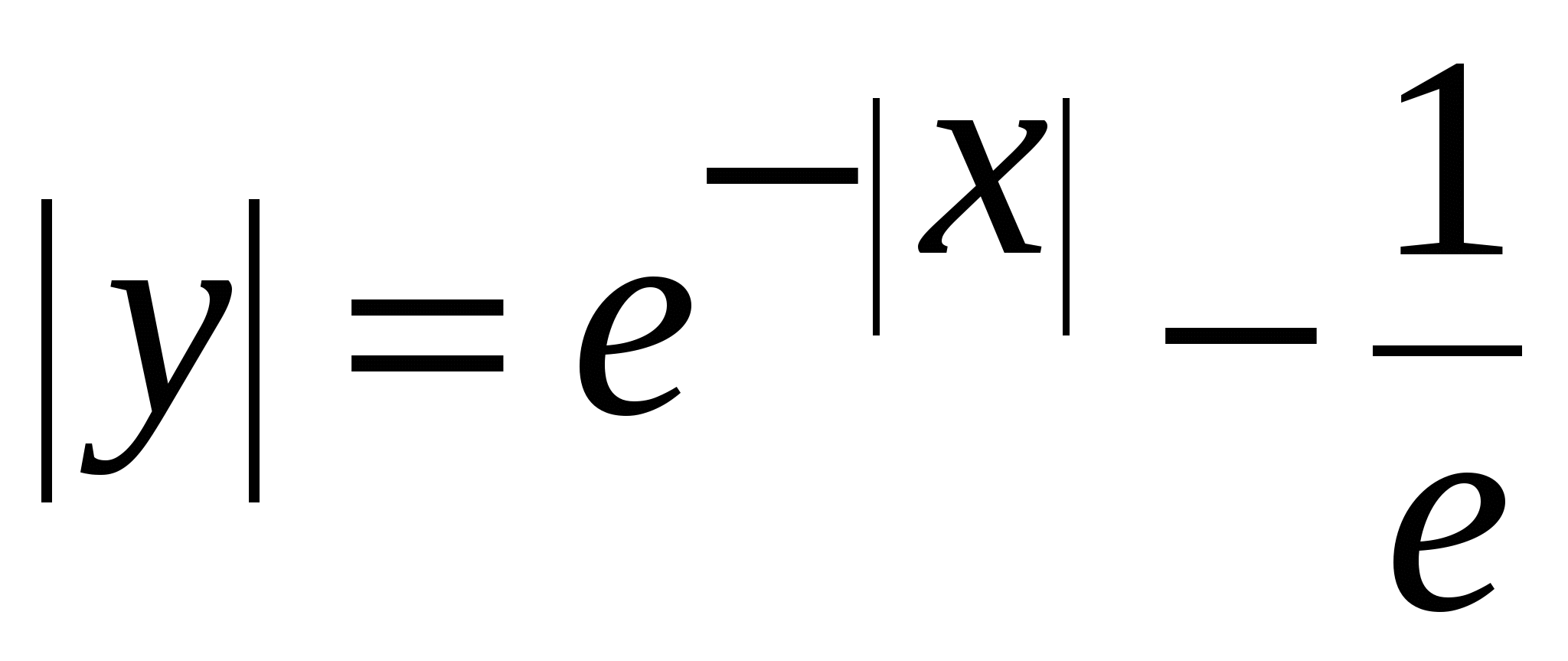 и найдите площадь фигуры, ограниченной такой линией. и найдите площадь фигуры, ограниченной такой линией.
Найдите площадь фигуры, ограниченной линиями 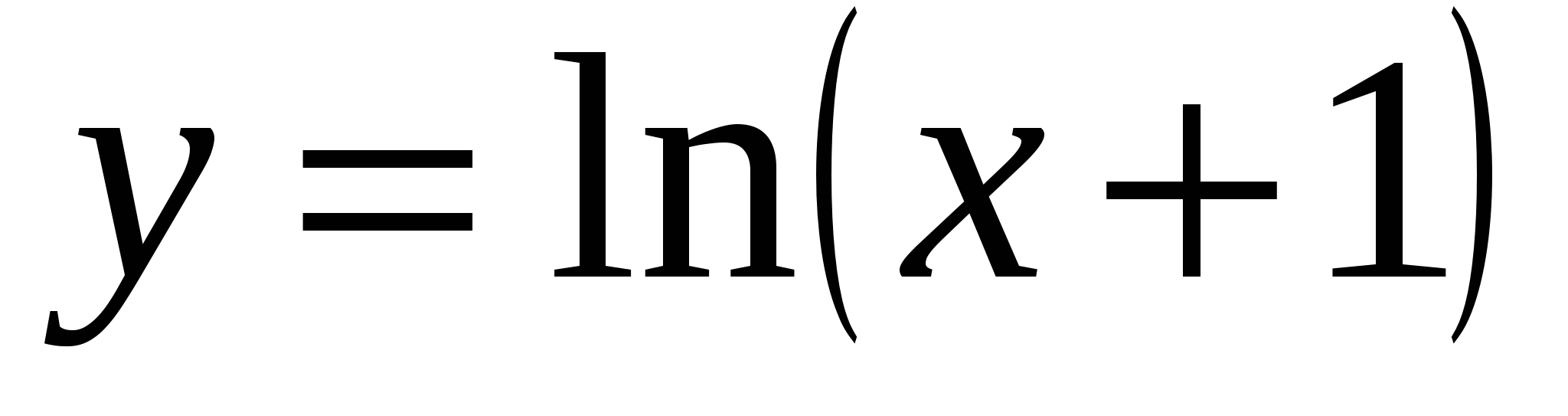 , ,  , ,  . .
При каком значении а площадь фигуры, ограниченной линиями  и и 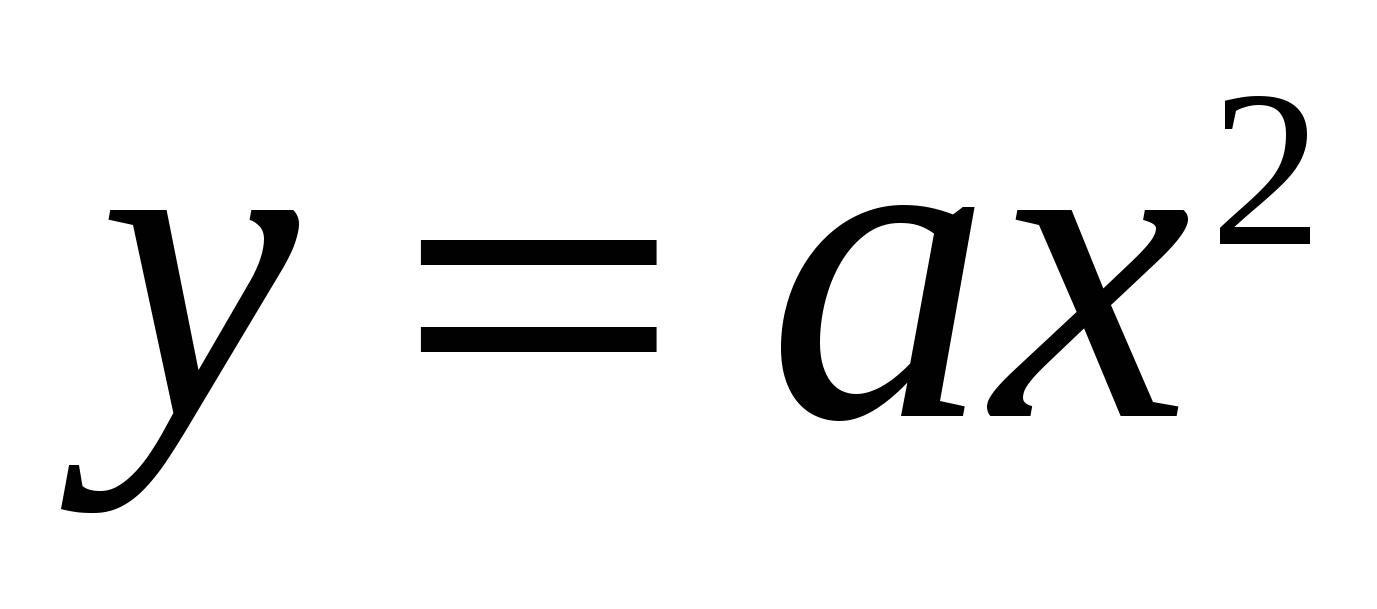 равна равна  ? ?
Найдите площадь фигуры, ограниченной графиком функции  и графиком её первообразной, имеющей с данным графиком общую точку на оси ординат. и графиком её первообразной, имеющей с данным графиком общую точку на оси ординат.
Найдите площадь фигуры, ограниченной графиком функции  и касательными к этому графику, проходящими через т. М (5;0) и касательными к этому графику, проходящими через т. М (5;0)
4.Самостоятельная работа.
Найдите площадь фигуры, ограниченной линиями:
I вариант
1.  , , 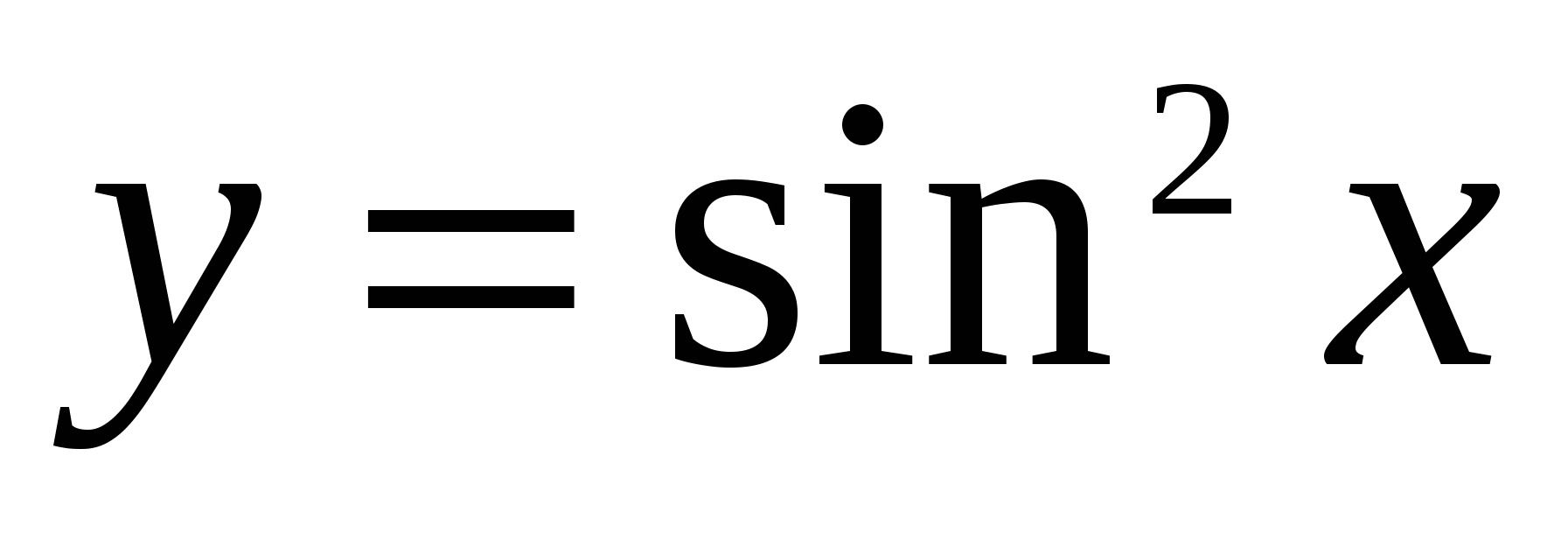 , где , где 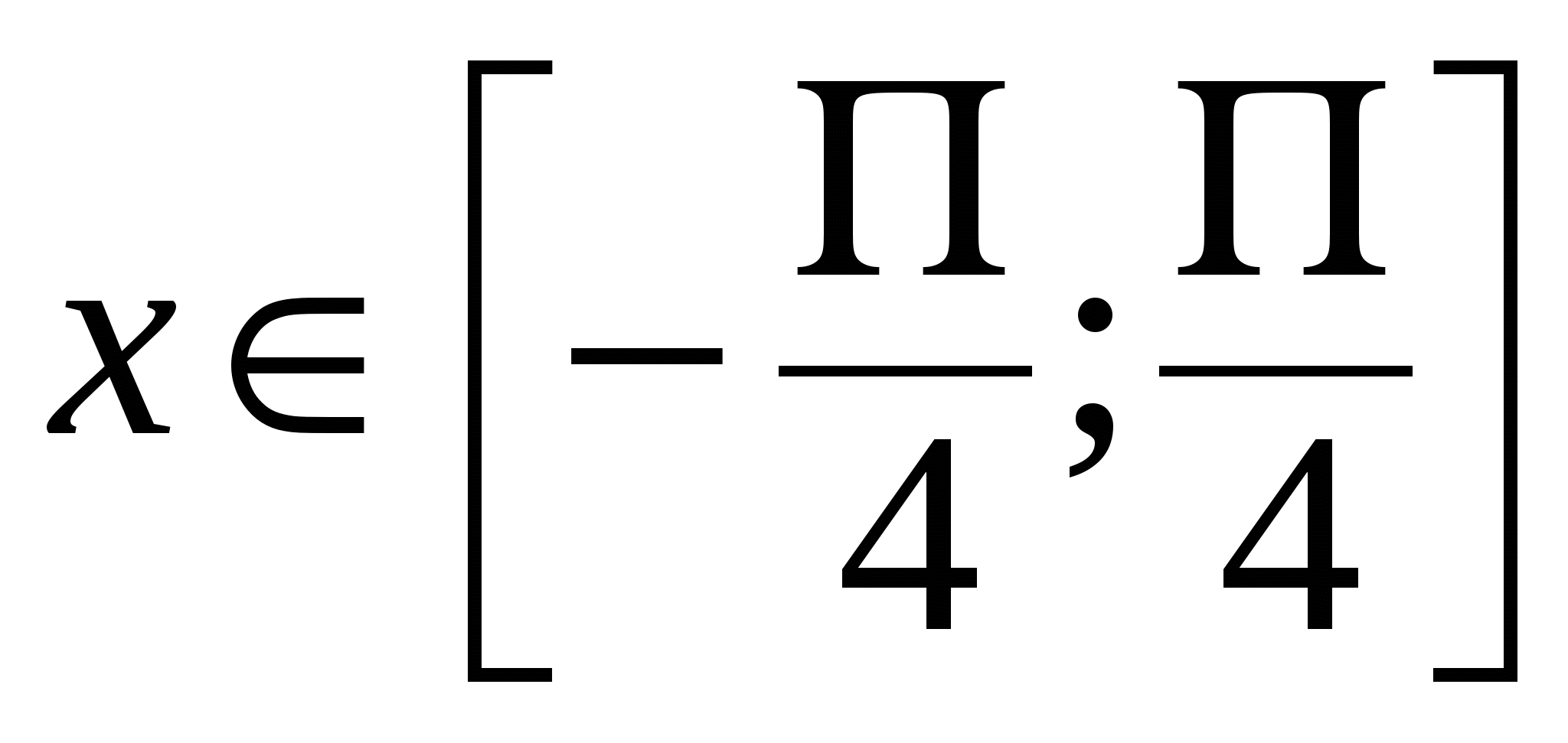 . .
2. 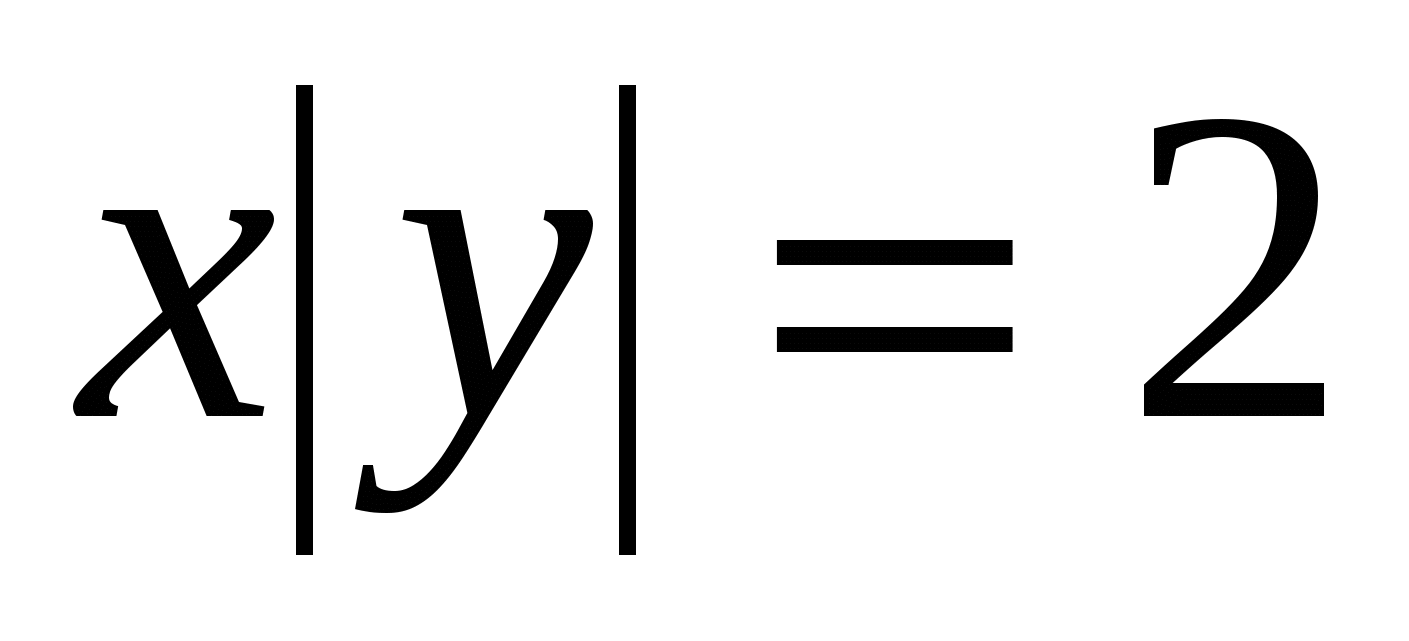 , , 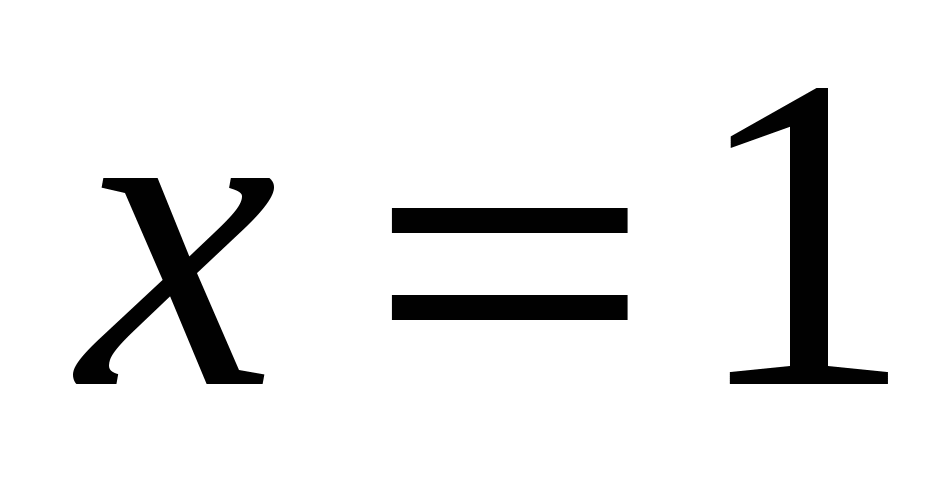 , , 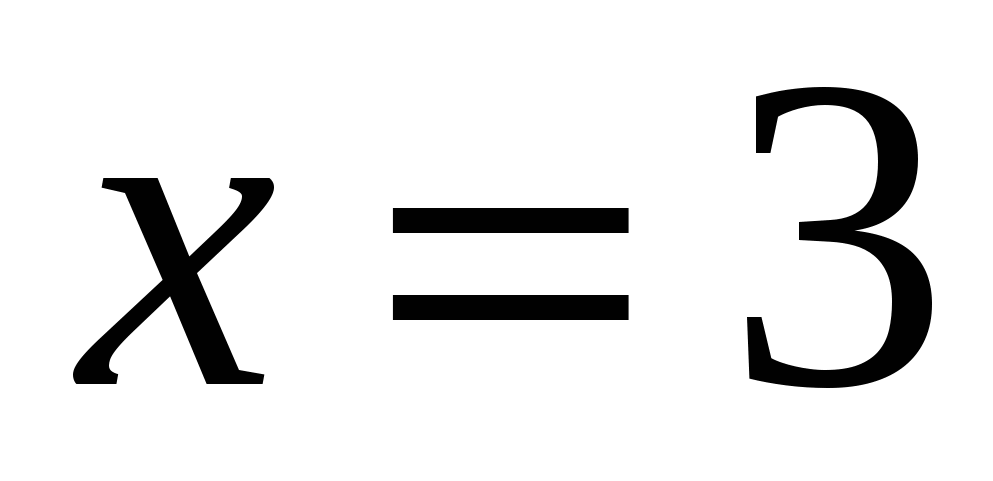 . .
3. 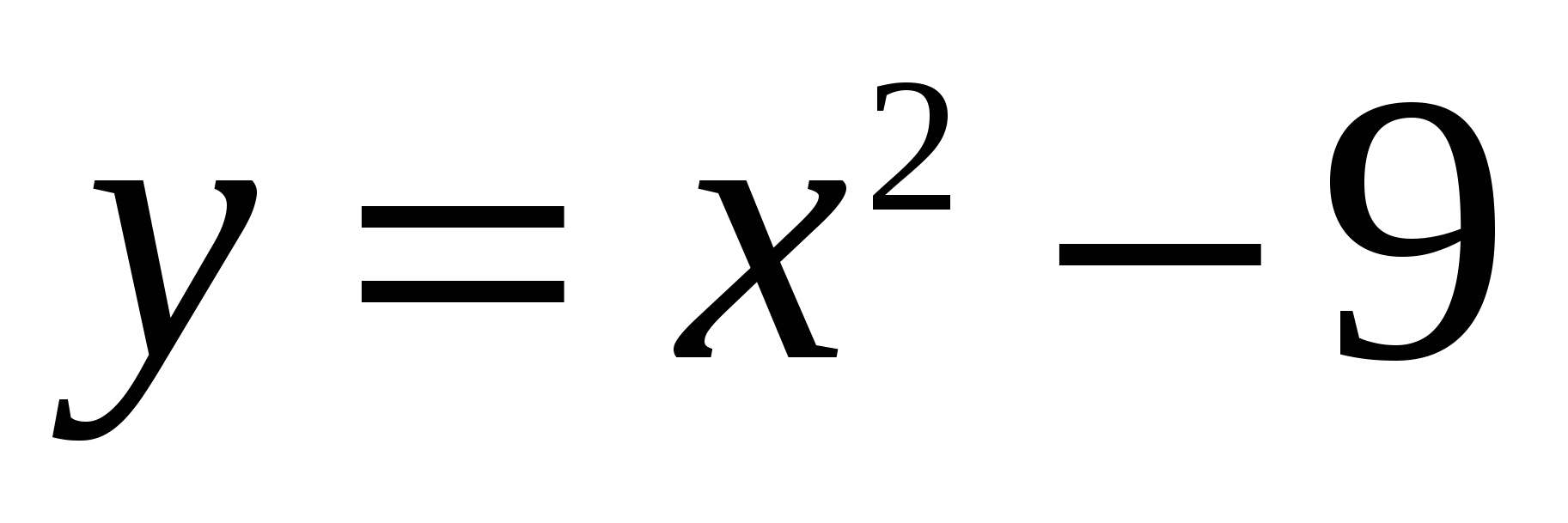 , ,  . .
II вариант
1. 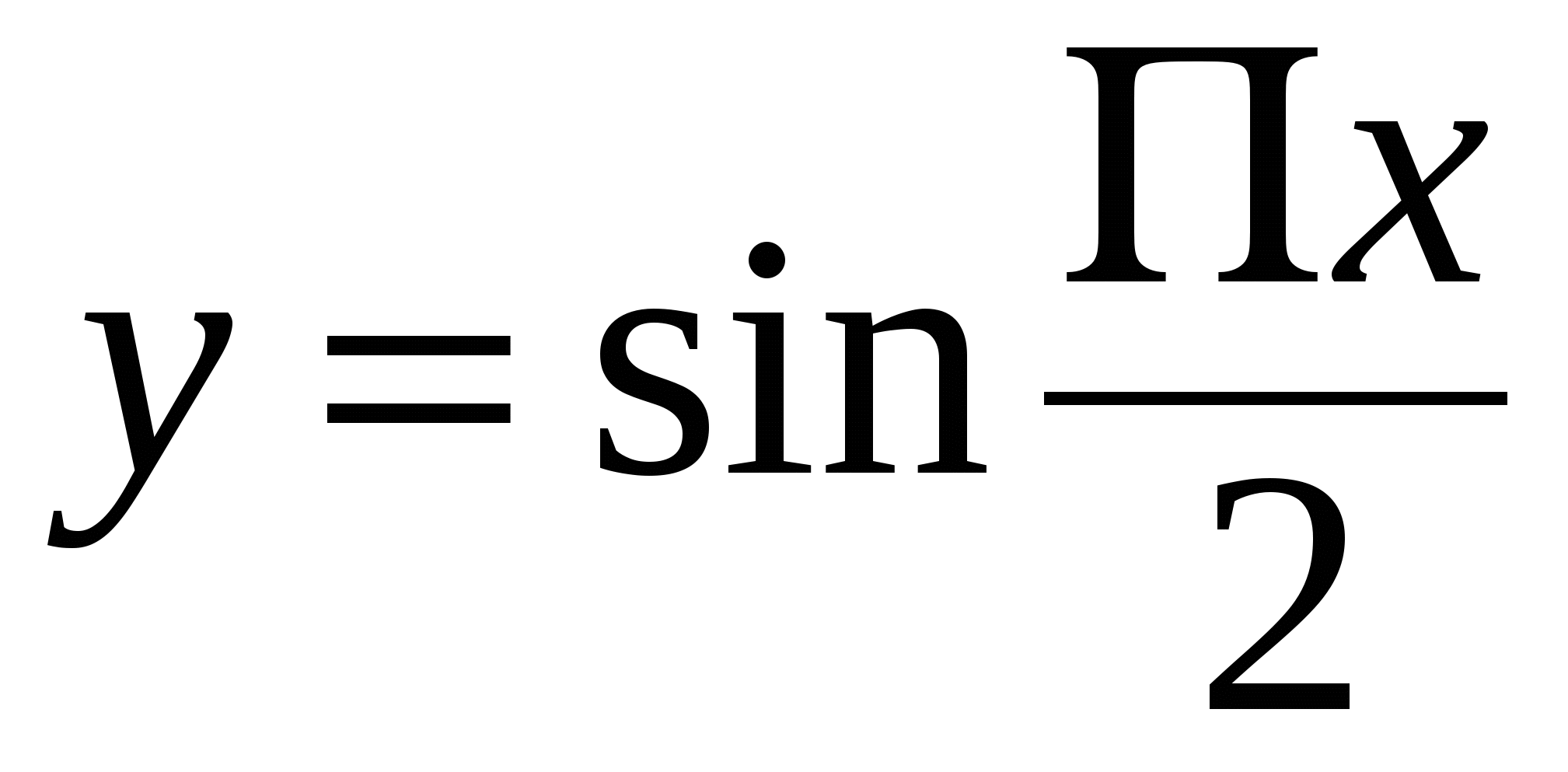 , , 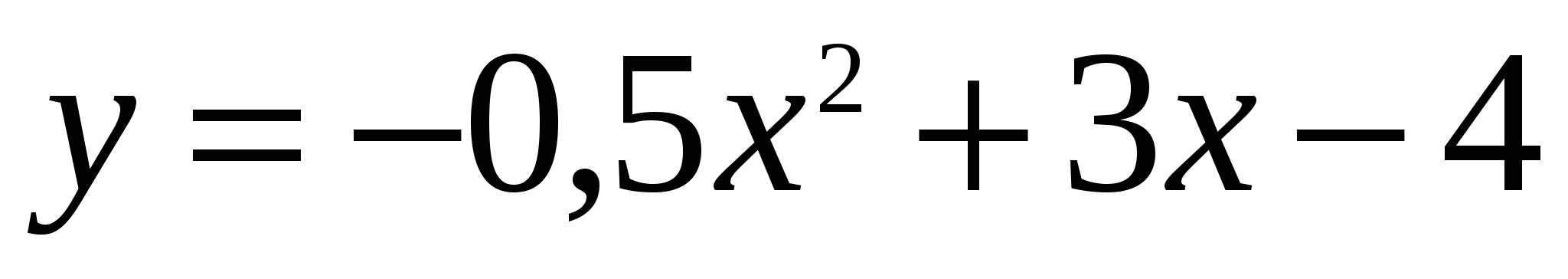 . .
2. 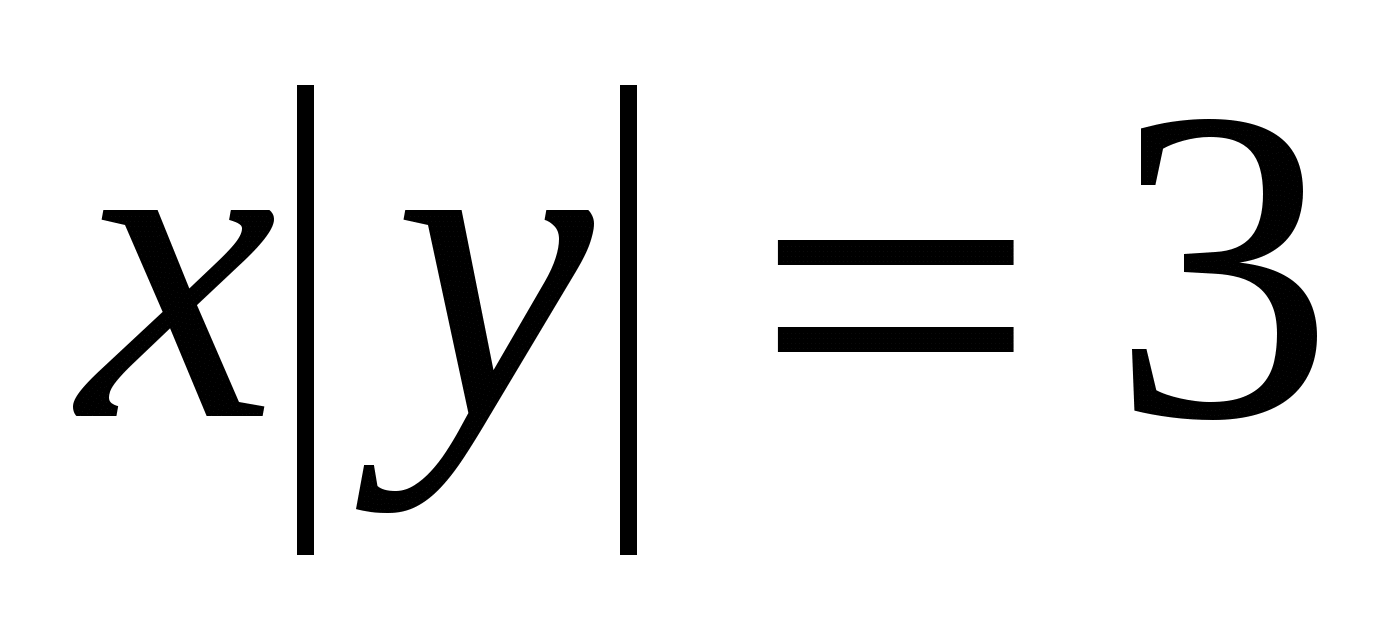 , , 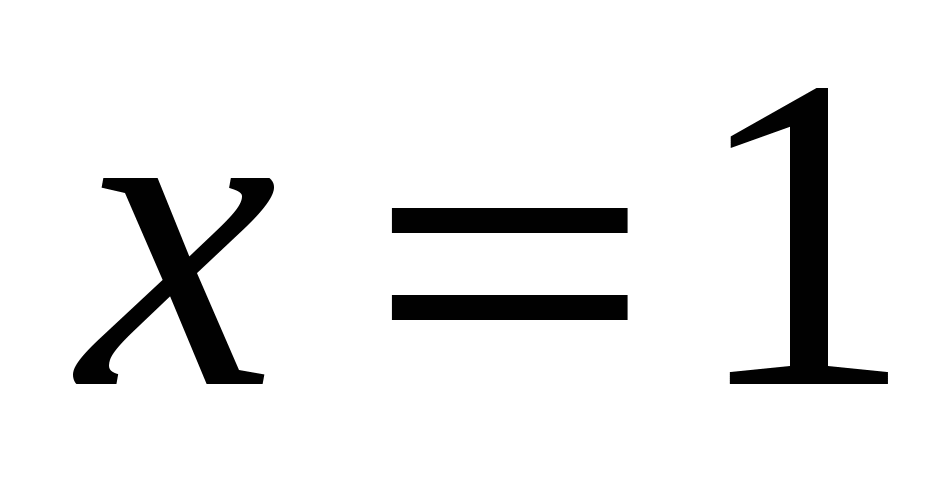 , , 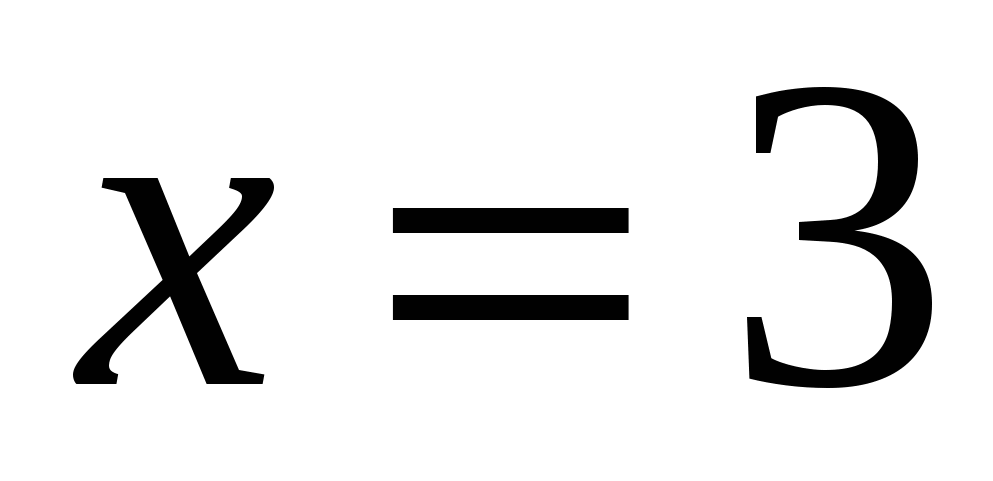 . .
3. 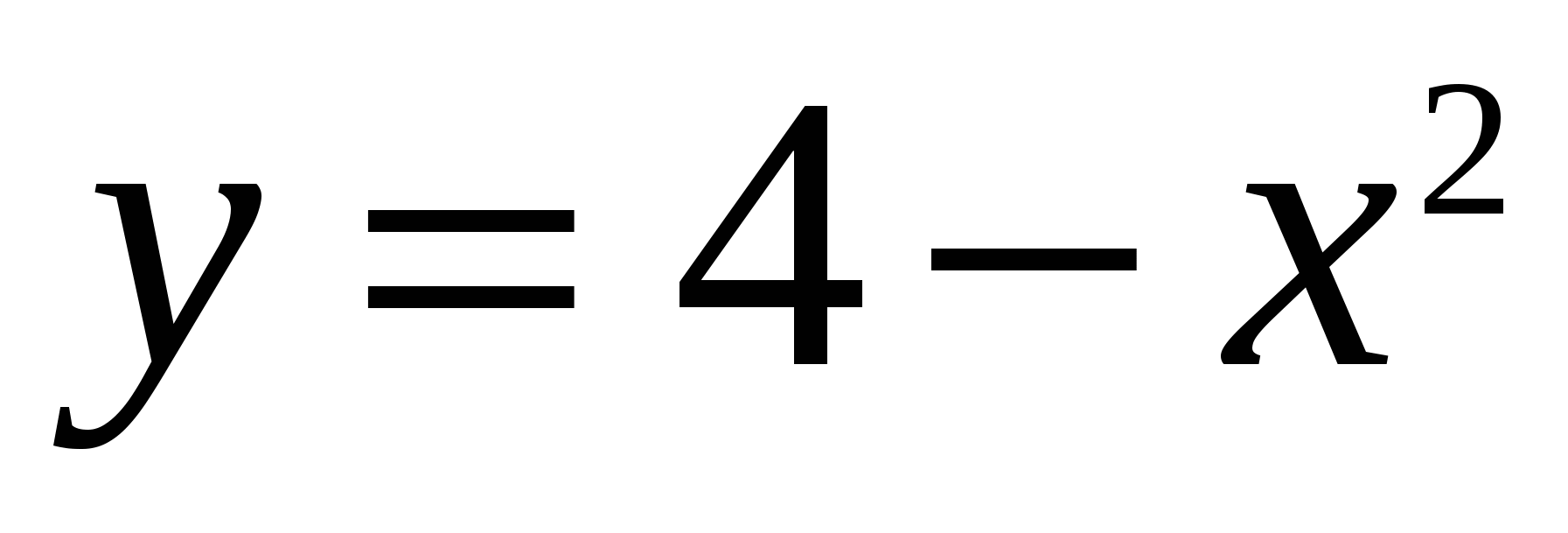 , ,  . . |
 Скачать 21.85 Kb.
Скачать 21.85 Kb.