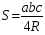Урока: проверка знаний учащихся по теме «Площади фигур»
 Скачать 95.12 Kb.
|
| Смотр знаний по геометрии в 8 классе проводится по теме «Площади фигур». Цель данного типа урока: проверка знаний учащихся по теме «Площади фигур» Задачи:
2. Углубить знания учащихся по теме. 3.Совершенствовать навыки общения. 4. Научить учащихся выступать перед аудиторией. Оборудование:
Подготовка к смотру знаний: О дате проведения и условиях проведения смотра знаний ребятам сообщается за три недели до начала мероприятия. Родителям рассылаются пригласительные билеты. За неделю до смотра в фойе школы вывешивается объявление, где указаны дата и время проведения смотра . Итоги смотра также вывешиваются в фойе. Ребята помогают в оформлении кабинета. За подготовку группы к смотру отвечает главный консультант, который систематически консультирует подготовку своих подшефных по отдельным вопросам, а «ненадежных» по всем. При этом повышается уровень и самих консультантов. Таким образом, он выясняет, как ребята готовятся к этому ответственному мероприятию. Старшеклассники также помогают ребятам готовиться к смотру, проводят консультации для тех, кто в этом нуждается. Таким образом, подготовка к смотру знаний имеет обучающее и большое воспитательное значение. Организация проведения смотра знаний: Смотр знаний проводится на двух итоговых уроках по данной теме. На него приглашаются родители, администрация школы, учителя. Родители имеют право, сидя за одним столом со своим ребенком, оказывать ему помощь в разумных пределах. Смотр знаний состоит из четырех этапов, которые должен пройти каждый ученик. За каждый этап он получает оценку по пятибалльной системе. В выставлении оценок каждому школьнику принимают участие учитель и члены жюри. Оценки выставляются в паспорт, который ученик получает в начале смотра. (Приложение 1) Возле каждого стола, а их четыре, сидит проверяющий – это хорошо подготовленный ученик из старших классов. Первый этап – доказательство теоремы по данной теме. Карточка с номером теоремы выбирается учеником. Второй этап – решение простейших задач. Из пяти задач как минимум надо решить три. В основном это задачи по готовым чертежам. Карточку с номерами задач вытягивает ученик.(работа по чертежам на интерактивной доске) Третий этап – решение более сложных задач, максимум надо решить две задачи, минимум – одну. Но желающие могут отказаться от этого этапа, а решать задачу из рубрики «Приз».Ответ оценивается тоже в 5 баллов. В эту рубрику включены сложные задачи, поэтому за ее правильное решение ученик получает приз и оценку «отлично». Четвертый этап – практическая работа. Задание для учащихся с низкими учебными возможностями : найти площадь фигуры, пользуясь теоремами о площадях известных фигур по готовой модели. Задание для учащихся творческого уровня: решить одну из задач с практическим содержанием. На смотре работает «Служба скорой помощи». В случае затруднения ученик может обратиться в эту службу не более одного раза, но если чаще, то оценка снижается на один балл. Как правило, ребята стараются без нее обойтись. В этот же день подводятся итоги по паспортам учащихся и бланкам жюри. Результаты сообщаются ученикам. Лучшие ученики поощряются. Задания, которые предлагаются учащимся для подготовки к смотру: К первому этапу смотра- теоремы и задачи с доказательством.
Окружности S=pr, где р – полупериметр треугольника.
Примерные задачи для подготовки ко второму этапу смотра. Задача 1. Вычислить высоту треугольника, если известны две его стороны и угол между ними. Например:1)16, 10, 600 2) 5,8, 300 3) 3,4; 8, 450 Задача 2. По двум известным сторонам и высоте, проведено к одной из сторон, найти другую высоту параллелограмма. Постройте вторую высоту параллелограмма и найдите её. 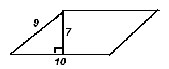 Задачи 3-7. Найдите площадь трапеции: 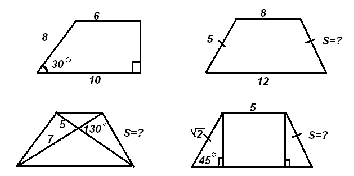 Задачи 8-9. Найдите площадь треугольника:  Задачи 10-11. Найдите площадь ромба: 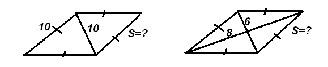 Комментарий: В течение всего периода подготовки к смотру учитель регулярно разъясняет вопросы из списка, которые показались ребятам непонятными. Для этого он выделяет время на уроках, так и после них. Ход смотраВступительное слово учителя: Ребята, у нас сегодня праздник Знаний, на который мы пригласили гостей: родителей, старшеклассников, учителей математики и администрацию школы. Перед вами стоит задача: показать свои знания по теме: «Площади фигур». Каждому из вас предстоит пройти четыре этапа. 1 этап – доказать теорему на выбор. 2 этап – устно решить не менее трех задач на выбор. 3 этап – решить письменно задачу с подробным объяснением на выбор или решение сложной задачи на приз. 4 этап – решить задачу с практическим содержанием ( на 5 баллов) или выполнить практическую работу, используя готовые модели ( на 4,3 балла). Оценивать ваши знания по теме будут члены жюри, в состав которого входит учителя математики и хорошо подготовленные старшеклассники. Доказательство теоремы заслушивают старшеклассники. Устное решение задач проверяет учитель математики №1, письменное решение задач проверяет учитель математики №2. Каждый член жюри имеет перечень вопросов и бланк для выставления оценок учащимся. У каждого из вас на руках имеется лист оценки, в который на каждом этапе смотра будут выставляться баллы. Познакомьтесь со шкалой оценки. ( Приложение 2.) На смотре работает «Служба скорой помощи». В случае затруднения вы можете обратиться в эту службу, но не более одного раза. Так же можно один раз воспользоваться помощью родителей. Желаю всем удачи! Задания для 1 этапа смотра на карточках.
Окружности S=pr, где р – полупериметр треугольника.
Задания для 2 этапа смотра:(чертежи предлагаются на интерактивной доске) 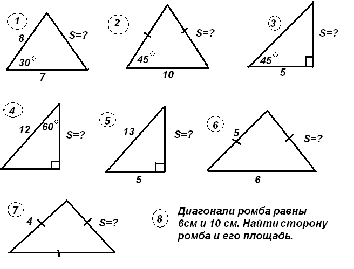 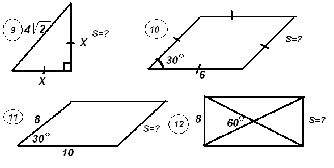 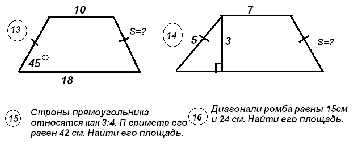 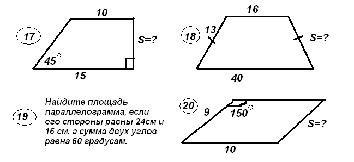 Комментарий: Устно опрашивает только учитель математики. Во время устной работы учащимся не рекомендуется поднимать руки. Учитель сам вызывает каждого очередного отвечающего. Это значительно экономит время урока и заставляет каждого быть внимательным. Учащиеся поднимают руку только тогда, когда требуется дополнить или исправить ответ. За три таких правильных выступления ученик зарабатывает 5 баллов. Если ответ можно дать по чертежу, то нужный рисунок проецируется на доску через кодоскоп. Устная работа с классом идет до тех пор, пока кто-нибудь из работающих по карточке не доложит о готовности к ответу. Учитель переключается на этого ученика. Как только подготовился следующий ученик у доски, к нему подходит один из членов жюри. С третьим учеником беседует другой член жюри и т.д. Тот учащийся, кто закончит ответ по карточке, присоединяется к работе класса. На его место учитель вызывает к доске другого ученика и снова предлагает ему выбрать карточку… Класс в это время выполняет письменные задания. Задания для 3 этапа смотра: Задачи первого уровня сложности. Задача 1. Боковая сторона равнобедренной трапеции 5 см, а ее диагональ делит среднюю линию на отрезки 3 см и 7 см. Чему равна площадь трапеции? Задача 2. В равнобедренную трапецию вписана окружность, касающаяся всех ее сторон. Боковая сторона трапеции равна 4 см, а угол при большем основании 300. Найти площадь трапеции. Задача 3. Найти площадь равнобедренного треугольника с основанием 24 см и боковой стороной 13 см. Задача 4. Площадь параллелограмма со сторонами 5 см и 6 см равна 24 см2. Найти диагональ параллелограмма. Задача5. В равнобедренном треугольнике основание равно а, а противолежащий ему угол равен 600. Найдите площадь треугольника. Задача 6. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями 600. Задача 7. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма , если одна его сторон равна 14 см, а один из углов 600. Задача 8. Вычислите площадь трапеции ABCD с основаниями AD и BC, если AD = 29 см, BC= 4см, AB= 16см. Угол А равен 300. Задача 9. Найдите сторону ромба и площадь ромба, если его диагонали равны 12 см и 16 см. Задача 10. Найдите площадь трапеции ABCD с основаниями AD и BC, если AD = 12 см, BC= 6см, CD= 5см, АС = 13 см. Задача 11. Найдите площадь равнобедренного треугольника, если его основание равно 10 см, а боковая сторона – 13 см. Задача 12. Стороны АВ и ВС треугольника АВС равны 8 см и 4,8 см, а высота, проведенная к стороне АВ, равна 6 см. Найдите высоту треугольника, проведенную к стороне ВС. Задачи второго уровня сложности – на «Приз» Задача 1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 300. Найти площадь параллелограмма. Задача 2. Основание равнобедренной трапеции равны 12 см и 16 см, а ее диагонали взаимно перпендикулярны. Найти площадь трапеции. Задача 3. Вычислить площадь трапеции с меньшим основанием 1 см, боковой стороной 3 см, составляющей с большим основанием угол 300,если другой угол при большем основании равен 450. Задача 4. Площадь параллелограмма со сторонами 5 см и 6 см равна 24см2. Найти две высоты параллелограмма. Задача 5. В прямоугольной трапеции ABCD с основаниями AD и BC боковая сторона АВ перпендикулярна большему основанию АD.Диагональ АС перпендикулярна CD. АD равно 24 см. Угол между АС и АD равен 600. Найдите площадь трапеции. Комментарий: Письменные ответы проверяет только жюри. Каждый ответ оценивается по пятибалльной системе. Задания для 4 этапа смотра Задания для учащихся с низкими учебными возможностями: Вычислить площадь фигуры, выполнив необходимые измерения.    Задачи для учащихся творческого уровня с практическим содержанием: Задача 1. Прямоугольная цветочная клумба занимает площадь 216 м2. Вдоль длинных сторон клумбы нужно проложить дорожки шириной 2 метра, вдоль коротких – шириной 3 метра. Каковы должны быть размеры прямоугольного участка (клумбы вместе с дорожками), чтобы площадь дорожек была наименьшей. Задача 2. Новосел, решив выложить пол в квадратной кухне площадью 7,29 м2 квадратными разноцветными плитками купил такой набор. Одна плитка со стороной 120см. Три плитки со стороной 90 см, девять плиток со стороной 60 см и две плитки со стороной 30 см. Другой новосел, для точно такой же кухни, купил на одну плитку больше со стороной 120 см, на одну плитку меньше со стороной 90 см и на одну плитку меньше со стороной 60 см. Кто из них поступил разумно? Задача 3. Поле имеет форму параллелограмма основание, которого 500 метров, а высота 180 метров. Через поле под прямым углом к основанию проходит шоссейная дорога шириной 12 метров. Найдите посевную площадь поля. Ответы к задачам Задача 1 – площадь дорожек наименьшая, когда ширина клумбы равна 12 метров, а длина 18 метров. Тогда размер прямоугольного участка ( клумбы вместе с дорожками) равен 24 X 16 м Задача 2 – более разумно поступил первый. Задача 3 – Посевная площадь равна разности площади параллелограмма АВСD и площади прямоугольника EFKT ( см. рисунок), т.е. S = SABCD – SEFKT = AD * ET – TK * EF = ET (AD – TK) ≈ 8 га. 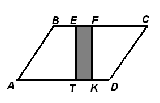 Подведение итогов смотра. Награждение лучших учащихся. Приложение1.
Приложение 2. Шкала оценки
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
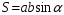
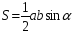
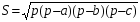, где р – полупериметр треугольника.