|
Задачи на максимум и минимум
Задачи на максимум и минимум
Представьте число52 в виде суммы трех положительных чисел так, чтобы сумма квадратов всех слагаемых была наименьшей, а отношение первого числа ко второму было равно 1:3.
Число 42 представьте в виде суммы трех положительных слагаемых так. Чтобы отношение первого числа ко второму было равно 3:4, а произведение всех трех чисел было наибольшим.
Произведение трех последовательных членов геометрической прогрессии с отрицательным знаменателем равно 343. Найдите наибольшую сумму этих трех членов среди всех прогрессий, обладающих указанными свойствами.
Участок в форме прямоугольника площадью 800 огорожен с трех сторон забором. Найдите наименьшую длину забора.
Периметр параллелограмма с острым углом 30˚ равен 4. Найти максимально возможное значение площади параллелограмма.
В пирамиде SABC ребра SA и BC образуют угол 60˚, SA=4, BC=6√3. Найдите наименьшую площадь сечения пирамиды плоскостью, параллельной SA и BC.
Определите наименьшую суммарную длину всех ребер прямоу�гольного параллелепипеда, полная поверхность которого равна 600 см2, если основание его является квадратом.
Дана прямоугольная система координат xOy. Какую наименьшую площадь может иметь прямоугольный треугольник, на гипотенузе которого лежит точка M (0;1), а катеты лежат на прямых x=-2 и y=0?
Автомобиль находится в степи в точке М, отстоящей от ближайшей точки А автотрассы на 60 км. Водитель должен попасть в точку В автотрассы, отстоящую от точки М на 110 км. Водитель подсчитал, что если он сначала доедет до точки С, которая находится на автотрассе между точками А и В, а затем по автотрассе до точки В, то на весь путь он потратит наименьшее время. Найдите расстояние от А до С, считая, что автомобиль движется по степи прямолинейно со скоростью 30км/ч, по автотрассе со скоростью 50км/ч, а автотрасса – прямая линия.
Имеются три сплава. Первый сплав содержит 10% золота, 40% серебра и 50% меди, второй – 20% серебра и 80% меди, третий – 20% золота, 30% серебра и 50%меди. Из них получили новый сплав, содержащий 5% золота. Какое наибольшее и какое наименьшее процентное содержание серебра может быть в новом сплаве?
Имеются три раствора. Первый содержит 80% спирта и 20% воды, второй – поровну глицерина и воды, третий – по 10% спирта и глицерина и 80% воды. Из них необходимо приготовить новый раствор, содержащий 40% воды. Какое наибольшее и какое наименьшее процентное содержание глицерина может быть в этом новом растворе?
Найдите все значения параметра a, при каждом из которых уравнение
x3-3x2-24x+a=0 имеет единственный корень.
При каком наименьшем значении a уравнение 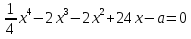 имеет ровно 2 корня? имеет ровно 2 корня?
При каком наименьшем значении а уравнение - х3 - 3х2 + 8 - а = 0 имеет ровно два корня?
Найдите все значения параметра р, при которых уравнение
р·ctg2 х + 2sin x + р = 3 имеет хотя бы один корень.
Найдите все значения параметра р, при которых уравнение
4sin3 х + 3cos 2х +р = 0 не имеет корней.
Найдите все значения параметра p, при которых уравнение
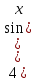 не имеет корней. не имеет корней.
Сравните числа π√10 и (√10)π .
Ответы:
8+24+20
12+16+14
-7
80
0.5
4
45км
pЄ(-∞;-3)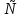 (7;+∞) (7;+∞)
π√10 < (√10)π
|
|
|
 Скачать 29.43 Kb.
Скачать 29.43 Kb.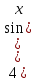 не имеет корней.
не имеет корней.