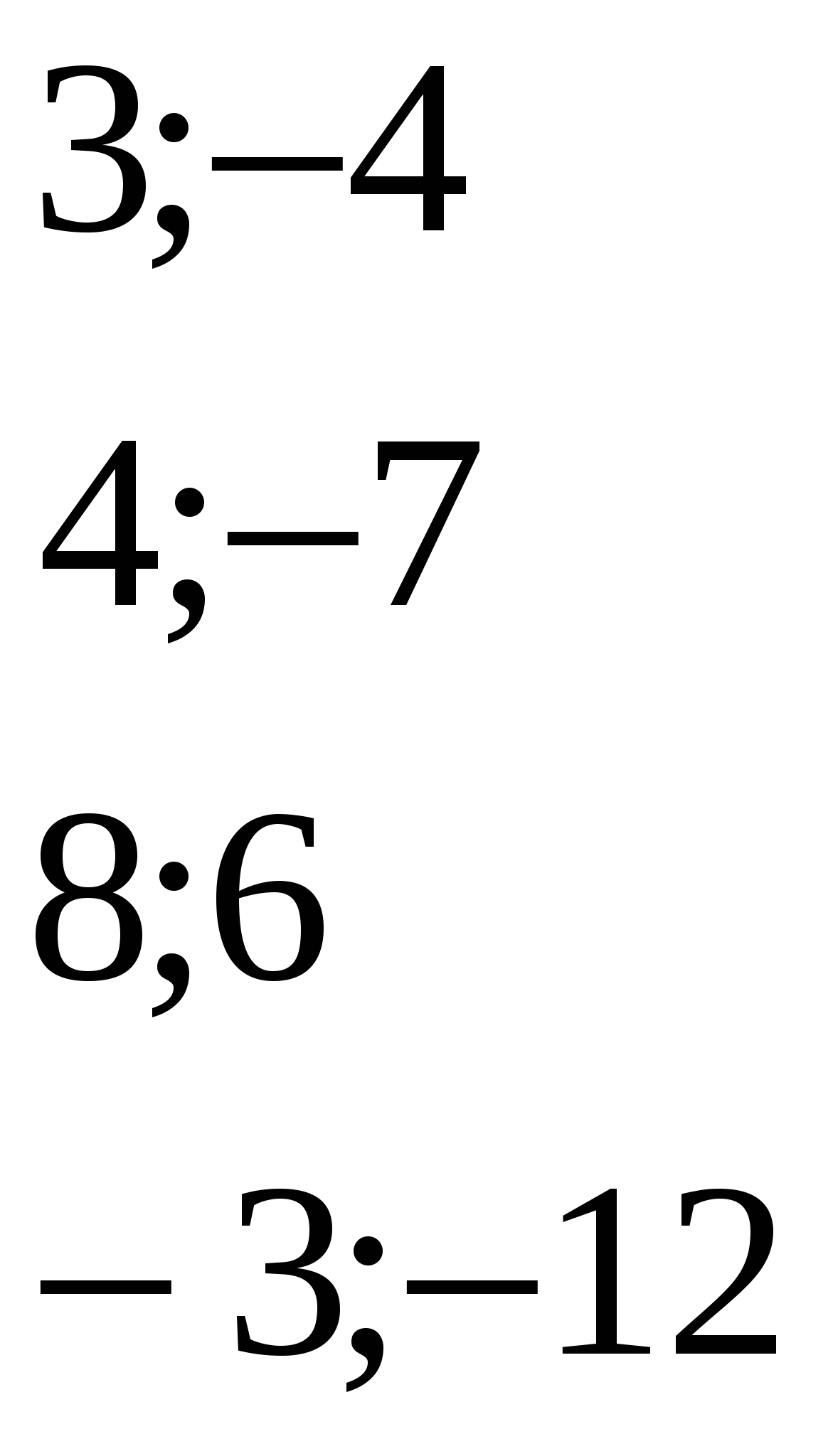Урок совершенствования новых знаний и способов действий. Образовательные цели

Название	Урок совершенствования новых знаний и способов действий. Образовательные цели
Дата	05.04.2016
Размер	49.99 Kb.
Тип	Урок

Приведенные квадратные уравнения.

Теорема Виета.

Тип урока: Урок совершенствования новых знаний и способов действий.
Образовательные цели:

1.«Открыть» зависимость между корнями и коэффициентами приведенного квадратного уравнения.

2.Рассмотреть применение теоремы Виета для приведенных квадратных уравнений в различных ситуациях.

Развивающие цели:

1.Формировать умения анализировать, обобщать и делать выводы.

2.Развивать интерес к математике, показав на примере жизни Виета, что математика может быть увлечением.

Воспитательные цели:

1.Формировать умение работать в соответствии с намеченным планом.

2.Воспитывать целеустремленность.

Оборудование:
Карточки для проведения самостоятельной, частично-поисковой деятельности учащихся, оформленная доска, ПК, проектор,
Структура урока.
1.Актуализация знаний.

1.Сообщение темы и целей урока.

2.Проверка домашнего задания.

3.Повторение основного теоретического материала, необходимого для изучения новой темы.

4.Постановка проблемной задачи.

2.Формрование новых знаний и способов действий.
1.Самостоятельная, частично-поисковая деятельность учащихся с целью выдвижения гипотезы о зависимости между корнями и коэффициентами приведенного квадратного уравнения.

2.Обобщающая беседа, подтверждающая выдвинутую гипотезу.

3.Доказательство теоремы Виета.

4.Историческая справка из жизни Виета.

3.Применение знаний, формирование умений и навыков.
1.Решение проблемной задачи.

2.Решение задач на применение теоремы Виета.

4.Итог урока.

5.Домашнее задание

Ход урока
На предыдущих уроках мы работали над темой «Квадратные уравнения». Изучили решение квадратных уравнений с помощью выделения квадрата двучлена, с помощью формул и рассмотрели, как используются квадратные уравнения при решении задач. Сегодня на уроке нам предстоит выяснить, какая связь существует между корнями и коэффициентами приведенного квадратного уравнения.

Начнем с проверки домашнего задания и повторения основного теоретического материала, необходимого для изучения новой темы.

Дома учащиеся должны были заполнить таблицу. Эта таблица изображена на доске. К доске вызывается один ученик с тетрадью и молча заполняет таблицу.

В это время проводится фронтальный опрос по следующим вопросам:

1.Сформулируйте определение квадратного уравнения.

2.Какое уравнение называется неполным квадратным уравнением?

3.Какое уравнение называют приведенным квадратным уравнением?

4.Что называют дискриминантом квадратного уравнения?

5.Сколько корней может иметь квадратное уравнение и отчего это зависит?

После опроса проверяется таблица, заполненная на доске.

Уравнение.	Корни.	Произведение корней.	Сумма корней.

Далее учащимся предлагается решить устно следующую задачу:
В уравнении конями являются числа 5 и -8. Найдите коэффициенты квадратного уравнения.
Учащиеся могут решить эту задачу, составив систему уравнений, но решить ее устно вызовет у них затруднение. Возникает вопрос: нельзя ли решить эту задачу, используя другой, более рациональный способ решения? Проблемная ситуация возникает при необходимости использования ранее усвоенных знаний в новой ситуации.

Поэтому завершением первого этапа урока является постановка учителем учебной проблемы: найти более рациональный способ решения задачи.

На этапе формирования новых знаний осуществляется самостоятельная, частично-поисковая деятельность учащихся. Эта работа проводится в парах постоянного состава по карточкам следующего содержания:
Дано приведенное квадратное уравнение:

1.Найти корни уравнения.

2.Найти сумму и произведение корней.

3.Сравнить сумму и произведение корней с коэффициентами уравнения.

4.Сформулировать предположение о связи между корнями приведенного квадратного уравнения и его коэффициентами.

5.Проверить свое предположение на других приведенных квадратных уравнениях, указанных в таблице.

6.Сделать вывод.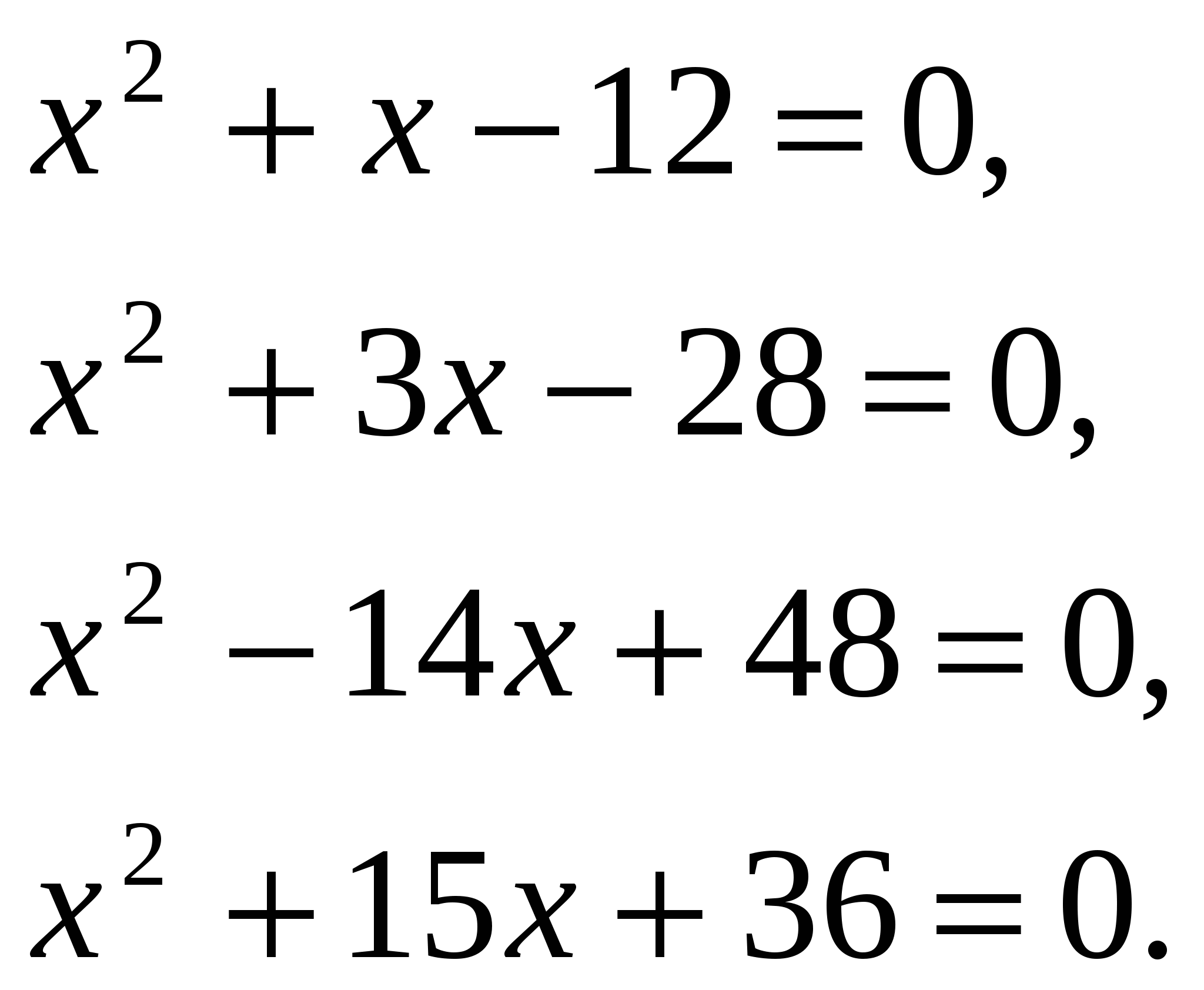

После того, как все задания будут выполнены, учащиеся выдвигают свое предположение и подтверждают его примерами из таблицы.

Учитель корректирует выдвинутую гипотезу и предлагает ученикам самостоятельно провести ее доказательство по аналогии с вопросами карточки. Он записывает на доске краткую запись условия и приглашает для доказательства ученика.

Дано:

Доказать:

Доказательство:

Если >0, то уравнение имеет два корня.

Если =0, то уравнение имеет один корень.

Если считать, что при =0 уравнение имеет два равных корня, то

теорема будет верна и в этом случае.

Если <0, то уравнение корней не имеет.

После доказательства учитель сообщает учащимся о том, что выдвинутая и доказанная гипотеза называется теоремой Виета по имени знаменитого французского математика Франсуа Виет.

Исторический материал. Затем, ребятам предлагается послушать мини-доклад о жизни этого математика, который подготовила ученица класса.

После этого внимание класса обращается к нерешенной в начале урока задаче. Теперь, используя теорему Виета, учащиеся решают эту задачу устно.

На этапе применения новых знаний учащимся предлагаются задания, записанные на доске.

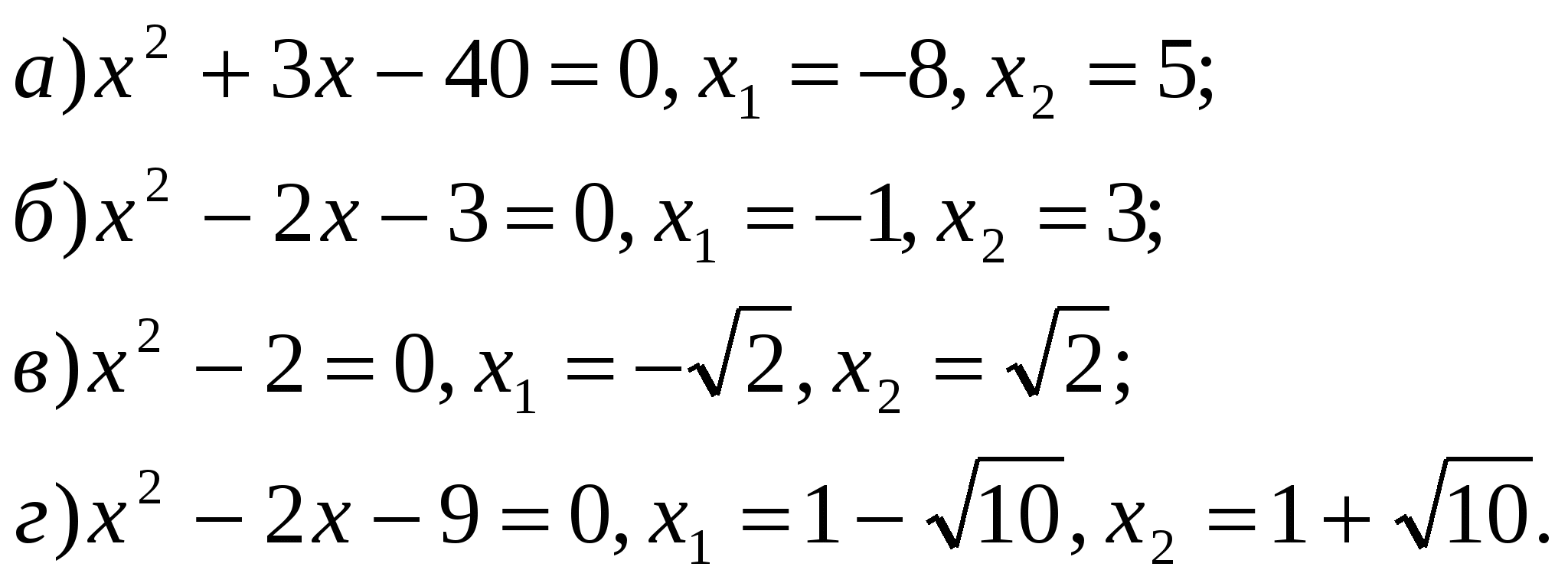Проверьте, правильно ли найдены корни квадратного уравнения:

2.Составьте квадратное уравнение, если его корни равны:

3.Можно ли назвать сумму корней квадратного уравнения

(Да. 2)

На самом деле ответ этот неверен, так как это уравнение корней вообще не имеет, потому что дискриминант отрицательное число.
V. Рефлексия

1.Что нового узнали на уроке?

2.Сформулируйте теорему Виета.

3.На примере, каких квадратных уравнений, сегодня на уроке, мы рассмотрели применение теоремы Виета?

4.Как можно использовать теорему Виета?

(Можно решать квадратные уравнения, можно проверять правильность решения квадратного уравнения.)

VI. Постановка домашнего задания.

П.3.6 -Выучить формулировку теоремы Виета

- на «5» выучить доказательство теоремы Виета.

№516(в,г), №520