«Графический способ решения квадратных уравнений»
 Скачать 115.74 Kb. Скачать 115.74 Kb.
|
| План–конспект урока по алгебре в 8 классе «Графический способ решения квадратных уравнений» 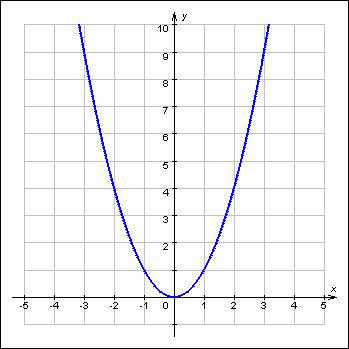 Учитель: Бирюков Павел Васильевич 2011-2012 уч.год Алгебра 8 класс Тема: «Графический способ решения квадратных уравнений» Цели урока: 1. Образовательные: познакомить учащихся с графическим способом решения квадратных уравнений, повторить ранее изученные методы решения квадратных уравнений, виды графиков и свойства функций у = 2. Развивающие: развивать навыки творческой, познавательной, мыслительной деятельности, логическое мышление, вырабатывать умение анализировать и сравнивать. 3. Воспитательные: воспитывать сознательное отношение к учебному труду, развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие. Оборудование: мультимедийный проектор, компьютеры, карточки с дифференцированными заданиями, сигнальные карточки. Тип урока: урок формирования знаний. Вид урока: урок – практикум. Методы урока: словесные, наглядные, практические. Организационные формы общения: индивидуальная, парная, коллективная. Структура урока: 1. Мотивационная беседа с последующей постановкой цели. 2. Актуализация опорных знаний – устная работа, с помощью которой ведётся повторение основных фактов, свойств на основе систематизации знаний. 3. Изучение нового материала – рассматривается ещё один способ решения квадратных уравнений – графический. 4. Закрепление изученного материала. 5. Практическая работа с использованием компьютеров. 6. Обогащение знаний – знакомство с траекториями движения космических аппаратов 7. Подведение итогов урока. 8. Творческое домашнее задание. 9. Рефлексия. Ход урока. I. Мотивационная беседа. Учитель: Как вы думаете, зачем надо изучать математику? Ответ на этот вопрос вы найдёте, если узнаете, что означает в переводе с греческого слово «математика». «Математика» - знание, наука. Именно поэтому, если человек был умен в математике, то это всегда означало высшую ступень учености. А умение правильно видеть и слышать – первый шаг к мудрости. Вот поэтому мне сегодня очень хочется, чтобы вы стали немного мудрее и расширили свои знания по математике. Цель урока - познакомить вас еще с одним способом решения квадратных уравнений – графическим, закрепить этот способ решения практической работой с использованием компьютеров. У вас находятся одинаковые трафареты, состоящие из 10 комбинаций, которые обозначены римскими цифрами. I II III IV V
VI VII VIII
IX X
В каждую клетку нужно вписать букву или знак препинания. Тогда сложится фраза. Но на трафарете нет места для самого первого слова зашифрованной фразы. Это слово мы получим, решив графические уравнения. У нас получится крылатое изречение из романа А. С. Пушкина «Евгений Онегин». Следует вам ответить на соответствующие тестовые задания I –X и вписать в трафарет знак или букву, которой обозначен верный ответ. Тестовые задания. II. Актуализация опорных знаний. 1. Линию, являющуюся графиком функции у = х2, называют… ?) синусоидой; :) гиперболой; …) параболой. I
2. Составьте слово, назвав подряд буквы, соответствующие правильному ответу. Является ли функция у = х2 возрастающей на отрезке [a; в], если: е) а = - 3; в = 3; к) а = 1; в = 4; д) а = - 2; в = - 1; а) а = 0; в = 0,5; к) а = 9; в = 10; б) а = - 9; в = 10; II
3. Назовите буквы, соответствующие точкам, принадлежащим графику функции у = х2 : М(3; 9), Ж(5; 5), С(-100; -100), Н(-2; 4), О1 (-1; 1), Г(0; 0), В(-7; 7), А(2; 8), О2(2; 4). III
4. Графиком функции а) прямая; б) отрезок; в) гипербола; г) ветвь параболы. IV
5. Назовите буквы, которые соответствуют правильному ответу. а) Какие из данных уравнений являются квадратными? в) 5х + 1 = 0. к) х3 – 2х2 + 1 = 0. н) 5 – 8х = 0. э) 2х2 – 9х + 5 = 0. з) 2х ─ т) 3х2 – 5х – 8 = 0. о) х2 + 5х – 6 = 0. V
б) Какие из данных квадратных уравнений являются приведенными? к) 2х2 – 9х + 5 = 0. в) х2 – 4х2 + 3 = 0. о) 3х2 + 5х + 2 = 0. л) 3х2 – 4х – 7 = 0. ф) 3х2 – 2х – 5 = 0. к) х2 + 6х + 8 = 0. з) х2 – 14х + 49 = 0. у) х2 – 10х + 25 = 0. е) х2 + 11х – 12 = 0. VI
III. Изучение нового материала. Решим уравнение: х2 + 2х – 3 = 0. Какое это уравнение? Как это уравнение можно решить? Ответ: С помощью формул, с помощью теоремы Виета. Можно его решить устно? Ответ: Можно, по теореме Виета. Какие же корни? Ответ: -3 и 1. Я сегодня покажу ещё один способ решения – графический. Представим данное уравнение в следующем виде: х2 = ─ 2х + 3. Чтобы решить данное уравнение, нужно найти такое значение х, при котором левая часть уравнения была бы равна правой. Введем две функции f(x), равной левой части уравнения и g(x), равной правой части уравнения. Теперь нужно найти такое значение х, при котором f(x)=g(x), т. е. общую точку, принадлежащую графику функции f(x) и графику функции g(x). Эта точка будет являться точкой пересечения графиков функций f(x)=х2 и g(x)=-2х+3. Абсцисса точки пересечения будет являться решением исходного уравнения. В координатной плоскости построим графики функций f(x) = х2 и g(x) = ─2х + 3. Для этого составим таблицы их значений. f(x) = х2 ─ парабола
[-3; 3] g(x) = ─2х + 3 ─ прямая
 А В  х = -3, х = 1. х = -3, х = 1. А(-3;9) и В(1;1)-точки пересечения. Абсциссы этих точек равны -3 и 1. Значит х = -3 и х = 1 – решение уравнения х2 + 2х – 3 =0 Ответ: так) х = ─ 1 и х = 3 для) х = ─ 3 и х = 1 вот) х = ─ 5 и х = 0 VII
Рассмотрим алгоритм решения. Алгоритм решения: 1. дано уравнение х2 + 2х – 3 = 0. 2. представим уравнение в следующем виде х2 = ─ 2х + 3. 3. в одной системе координат строятся графики функций у1 = х2 и у2 = ─ 2х + 3. 4. абсциссы точек пересечения являются решением данного уравнения IV. Закрепление изученного материала. 1). Решить уравнение х2 – х – 2 = 0. x у1 = х2 у2 = х + 2 Ответ: души) х = - 2 и х = 1 школы) х = 3 и х = 1 сердца) х = 2 и х = - 1. VIII
2). Решить самостоятельно.
а) один ученик решает графически; б) другой ученик решает аналитически с помощью теоремы Виета. Ответ : широкого) х = 5 и х = 1; русского) х = 4 и х = - 2; красного) х = 3 и х = - 1. IX
а) один ученик решает графически; б) другой ученик решает аналитически с помощью квадратных корней Ответ: слилось) х = 1 и х = -1,5; расцвело) х = 3 и х = - 2; приснилось) х = -1 и х = 2. X
Физминутка. Отвели свой взгляд направо, Отвели свой взгляд налево, Оглядели потолок, Посмотрели все вперёд. Раз – согнуться – разогнуться, Два ─ согнуться – потянутся, Три – в ладоши три хлопка, Головою три кивка. Пять и шесть тихо сесть. V. Практическая работа. Раздаются учащимся дифференцированные задания на карточках. С помощью графиков нескольких функций, построенных на заданных промежутках, получаются буквы: М; О; С; К; В; А. и фигуры: КИТ; ЗОНТИК; ОЧКИ. (см. приложение к уроку). Учитель: Какие буквы у вас получились? Ответы учащихся: М О С К В А Учитель: Получилась фраза А.С. Пушкина из романа «Евгений Онегин» «Москва… как много в этом звуке для сердца русского слилось». (Как часто в горестной разлуке, В моей блуждающей судьбе, Москва, я думал о тебе! Москва … как много в этом звуке Для сердца русского слилось! Как много в нём отозвалось.) VI. Обогащение знаний. Высвечивается слайд, на котором находится парабола и гипербола. а) мы сегодня на уроке применяли эти два графика: параболу и гиперболу. Я хочу вам сказать ребята, что окружающий нас мир тесно связан с математикой. Валерий Чкалов говорил: «Полёт–это математика». Оказывается, траектории движения космических аппаратов описываются параболой, гиперболой, эллипсом. При первой космической скорости (7,91 км/с) космический аппарат движется по эллипсу относительно Земли. (на рис. орбита 3) При второй космической скорости (11,2 км/с) аппарат движется по параболе (на рис. орбита4) и движется в пределах Солнечной системы. При третьей космической скорости (16,6 км/с) космические аппараты движутся по гиперболе (на рис. орбита5) и навсегда покидают пределы Солнечной системы. В 70-х годах ХХ века были запущены такие космические аппараты «Пионер-10», «Пионер-11»,которые навсегда покинули Солнечную систему в поисках разумных цивилизаций во Вселенной. Они несут в себе платиновые пластинки, на которых нанесены силуэты мужчины и женщины на фоне космического корабля, Солнечная система и траектория «Пионера», схема атома водорода и положение Солнца по отношению к наиболее ярким галактическим пульсарам. б) графики помогают нам наглядно увидеть изменения различных величин: изменение роста, веса, температуры, скорости и т.д. Вот посмотрите на эти графики, характеризующие ваш класс: 1. График успеваемости (Знание – сила. Кто много читает, тот много знает – пословица. 2. График роста, график веса учащихся 8-го класса. Чтобы достичь нормального веса и роста подростку 15-ти лет нужно заниматься спортом, вести здоровый образ жизни, не увлекаться пагубными привычками: алкоголем, табакокурением, наркотиками. Никогда не забывать пословицу «В здоровом теле здоровый дух» VII. Подведение итогов урока. Вы замечательно поработали на уроке. Проверив ваши работы и учитывая ваши ответы за устную работу, я поставила вам оценки в индивидуальную таблицу. Каждый ученик класса принимал участие в уроке. Во время урока заполняется индивидуальная таблица, в которой виден результат его работы на уроке.
Надеюсь, этот материал вы не забудете. Помните слова французского инженера-физика Лауэ: «Образование есть то, что остается, когда все выученное уже забыто». Думаю, что образование, которое вы получите, будет соответствовать времени, в котором мы живем. А чтобы это случилось на самом деле, предлагаю вам выполнить следующую творческую домашнюю работу. VIII. Домашнее задание. Творческое задание: составить рекламу параболе или гиперболе; сочинить сказку или рассказ на тему «Замечательные кривые». IX. Рефлексия. В конце урока проводится беседа, в которой выясняется: - Что нового узнали на уроке? - Понравился ли урок? (с помощью сигнальных карточек) - Что понравилось на уроке? - Что не понравилось? - Что необходимо изменить, чтобы было еще интереснее? |