Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача


«Правила вычисления производных»



Скачать 78.47 Kb.
Название«Правила вычисления производных»
Дата05.03.2016
Размер78.47 Kb.
ТипДокументы

Тема: «Правила вычисления производных»

Цели урока:

Оборудование:

  • ПК учителя, мультимедийный проектор.

  • Индивидуальные карточки для проведения самостоятельной работы.

  • Презентация, содержащая материал для повторения и закрепления теоретических знаний, для фронтального опроса по теории.


I этап урока – организационный

Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится у них на парте.

II этап урока – повторение теоретического материала по теме «Правила вычисления производных»

Учитель: «А теперь вспомните формулы производных элементарных функций и сформулируйте правила вычисления производных:

- производная постоянной функции;

- производная линейной функции;

- производная степенной функции;

- производные тригонометрических функций;

- производная экспоненты;

- производная натурального логарифма;

- производная сложной функции, зависящей от линейной;

- производная суммы функций;

- производная произведения функций;

-производная частного функций».


C′ = 0 (kx + m)′ = k =



= =

= =

= =



На слайдах № 2, 3 появляются соответствующие формулы по мере ответов учащихся.
Слайд № 2
Слайды 4 -9


III этап урока – работа в тетради по теме урока (карточки на парте)

В классе выполнить №2,5,7,9,10,15,20

Найти производную функции ( 1 – 4; 7; 8 ):









  5. Укажите абсциссу точки графика функции в которой угловой коэффициент касательной равен 2.

  6. Найдите значение производной функции в точке .





  9. Решите неравенство , если

  10. Решите уравнение , если

  11. Найдите тангенс угла наклона касательной, проведенной к графику функции в его точке с абсциссой .

  12. Найдите угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой 2.

  13. Дана функция . Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.

  14. Тело движется по прямой так, что расстояние S (в метрах) от него до данной точки М этой прямой изменяется по закону (t – время движения в секундах) Найти скорость и ускорение в момент .

Найдите значение производной в заданной точке ( 15 – 17 ).

  1. ;

  2. ;

  3. ;

  4. Найдите угловой коэффициент касательной к графику функции , проведенной к точке с абсциссой 1.

  5. Найдите тангенс угла наклона касательной, проведенной к графику функции в его точке с абсциссой .

  6. Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .

  7. Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .

  8. Укажите число целых решений неравенства , если .


Ответы:


1.
2.
3.
4.
5.
6.
















2,5




7.
8.
9.
10.
11.
12.


7






0

8

2



13.
14.
15.
16.
17.
18.






21м/с; 24м/с2

1

-6

1

8



19.
20.
21.
22.


-6

7,5

4,5

9


IV этап урока – самостоятельная работа

Вариант 1

  1. Вычислите значение производной функции в точке .




  1. Найдите производную функции .



  1. Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .





















  2. На графике функции взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси ОХ под углом, тангенс которого равен 5. Найдите абсциссу точки А.



5. На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке .

Вариант 2

  1. Найдите значение производной функции в точке с абсциссой .

  2. Найдите производную функции .




  1. Найдите угловой коэффициент касательной, проведенной к графику функции в его точке с абсциссой .




  1. Определите абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс.

1)
– 8
2)
1
3)
0
4)
4



5. На рисунке изображен график функции и касательная к нему в точке с абсциссой . Найдите значение производной в точке .



Ответы:

Номер задания
1
2
3
4
5

Вариант 1
2
1
3
4
1,5

Вариант 2
4
3
1
2
−1


V этап урока – историческая справка по теме урока (презентация № 2)

Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла.

В 1679 году Пьер Ферма находил экстремумы функции, касательные, наибольшие и наименьшие значения функций. Но в своих записях он использовал сложнейшую символику Виета, и поэтому эти исследования не привели к созданию теории интегральных и дифференциальных исчислений.

В 1736 году Исаак Ньютон получил теорию интегральных и дифференциальных исчислений методом флюксий (производных). Но вся теория была осмыслена с точки зрения физики. Математики хотели строгих логических обоснований.

Современник Ньютона Лейбниц предложил новый подход к математическому анализу. Он ввёл обозначения дифференциала, интеграла, функции, такие понятия как ордината, абсцисса, координата. Но в его теории было много “тёмных мест”.

И вот в 18 веке величайший математик Леонард Эйлер создал теорию дифференциальных и интегральных исчислений, и в таком виде она изучается и по сей день.

VI этап урока - подведение итогов, комментарии по домашнему заданию.

В качестве домашнего задания учащиеся получают карточки, работу с которыми начали на уроке. Дома № 1,3,4,6,12,16
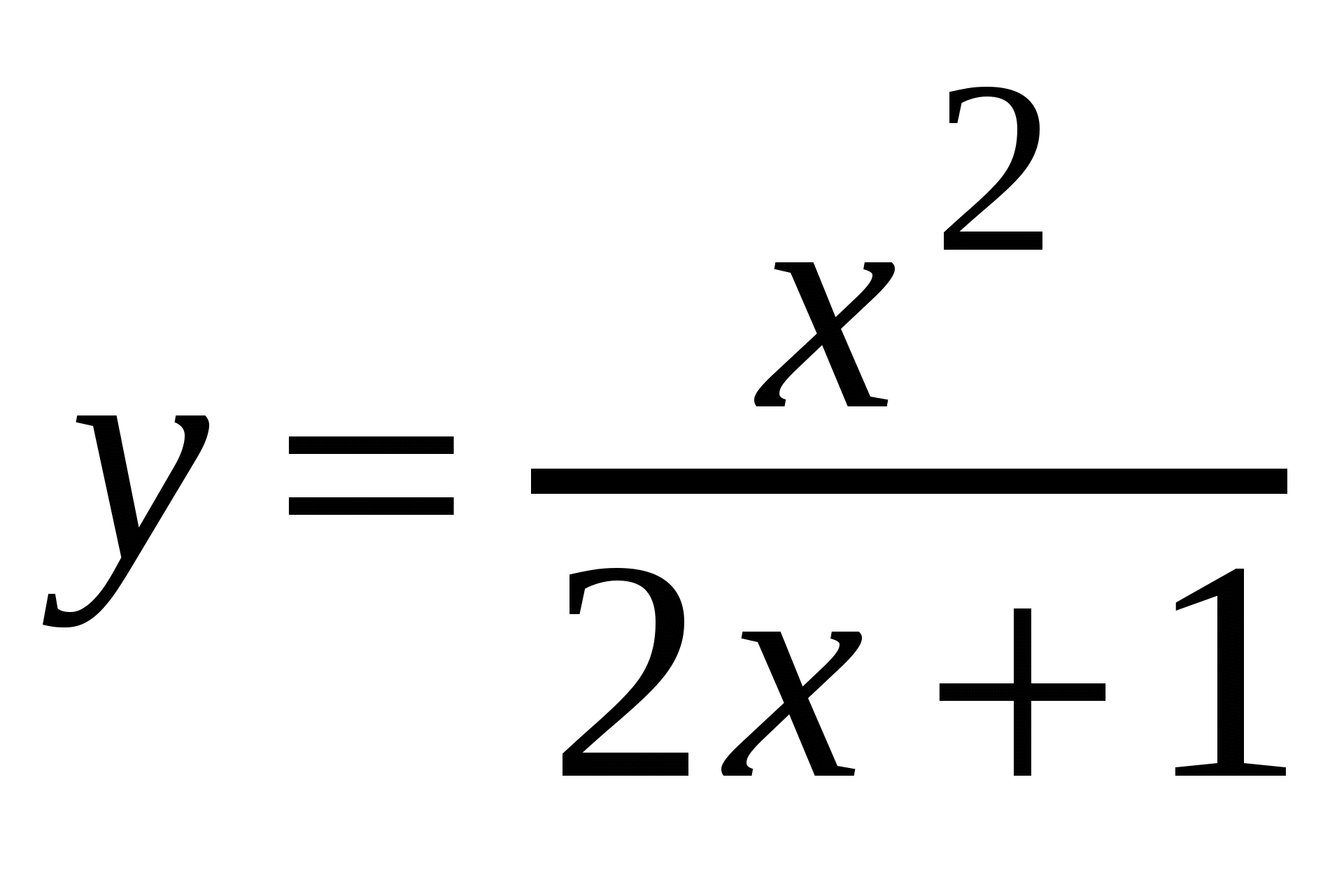