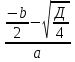|
Способы решения квадратных уравнений
Урок математики в 8 классе
Тема: Способы решения квадратных уравнений.
Тип урока: урок изучения новых знаний.
Цель урока:
Образовательная: формирование умений применять полученные ранее знания, сопоставлять, анализировать, делать выводы, отработка умения решать уравнения.
Развивающая: создание условия для самостоятельного получения новых знаний, для развития наблюдательности, памяти, логического мышления.
Воспитательная: создание условий для формирования интереса к познавательному процессу, для воспитания культуры общения в парной и групповой работе.
Ожидаемый результат: каждый ученик должен ознакомиться с пятью способами решения квадратных уравнений и уметь решать их, выбрав тот способ, который для него более приемлем.
План урока.
Этап
|
Дидактические задачи
|
Деятельность
учителя
|
Деятельность учащихся
|
Ведущий метод
|
ФОПД
|
I
2 мин
|
Организовать работу школьников на уроке
|
Побуждает школьников к организации своего рабочего места
|
Самоорганизация
|
Словесный
|
Фронтальная
|
II
4 мин
|
Подготовка учащихся к восприятию изучаемого материала
|
Создание мотивации деятельности, обоснование выбора темы
|
Слушают
|
Словесный
|
Индивидуальная
|
III
7 мин
|
Установить степень усвоения ранее полученных знаний
|
Организует работу учащихся по применению знаний в стандартной ситуации
|
Работают с таблицей, отвечают на вопросы, пишут графический диктант
|
Репродуктивный
|
Индивидуальная, фронтальная
|
IV
2 мин
|
Обеспечить включение учеников в деятельность по получению новых знания
|
Проводит инструктаж по выполнению работы
|
Слушают
|
Словесный
|
Фронтальная
|
V
10 мин
|
Получение новых знаний
|
Наблюдает и оказывает помощь
|
Самостоятельная работа в группах по инструкции
|
Частично-поисковый, поисковый
|
Групповая
|
VI
15 мин
|
Усвоение новых знаний
|
Наблюдает, корректирует деятельность учащихся
|
1 человек из группы объясняет у доски, остальные работают в тетрадях
|
Объяснительный, познавательный
|
Индивидуальный
|
VII
4 мин
|
Анализ и оценка успешного достижения цели и перспектива следующей работы. Мобилизация учащихся на рефлексию
|
Даёт анализ и оценку успешности достижения цели
|
Взаимооценка результатов работы в группах
|
Создание ситуации успеха
|
Фронтальная
|
VIII
1мин
|
Обеспечение понимания цели и содержания выполнения домашнего задания
|
Даёт инструктаж по выполнению домашнего задания
|
Воспринимает на слух
|
Словесный
|
Фронтальная
|
I. Историческая справка. Доклад об истории возникновения квадратных уравнений.
II. Повторение. Работа с таблицей.
№
|
а
|
b
|
c
|
1
|
-2
|
5
|
0
|
2
|
1
|
0
|
16
|
3
|
2
|
6
|
-8
|
4
|
3
|
-5
|
6
|
5
|
-1
|
4
|
0
|
Ответить на вопросы: назвать полные, неполные, приведённые уравнения.
III. Проверить правильность утверждений и составить цифровую картину:
1 – верно
0 – неверно
Квадратным называется уравнение вида: a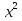 +bx+c=0, где a, b, c – числа, а ≠0, х – переменная. +bx+c=0, где a, b, c – числа, а ≠0, х – переменная.
Уравнение называется неполным, если один из его коэффициентов равен нулю.
Уравнение называется приведённым, если а=1.
Если Д < 0, уравнение имеет два корня.
Если Д = 0, уравнение имеет один корень.
IV. Работа в группах
Группа №1.
Решение уравнений с чётным коэффициентом b/
3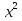 +2x-5=0 +2x-5=0
3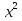 +8x-3=0 +8x-3=0
-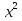 +2x+8=0 +2x+8=0
5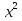 -8x-4=0 -8x-4=0
Инструкция.
Выпишите коэффициенты a, b, c.
Найдите по формуле 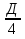 = ( = (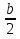 )2 - ac )2 - ac
Найдите по формуле x1 = 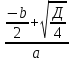 x2 = x2 = 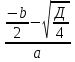
Группа №2.
Решение уравнений методом разложения на множители.
Инструкция.
Внимательно прочитайте решение уравнения x2+10x-24 = 0
Представим слагаемое 10x как разность 12x и 2x: 10x = 12x-2x
Получим х2 +12x -2x -24 = 0. Из каждой пары слагаемых вынесем общий множитель:
X2 + 12x -2x -24 = 0
x (x+12) - 2(x+12) = 0
(x+12) (x-2) = 0 Произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю.
x+ 12 = 0 или x-2 = 0.
x = -12 или x = 2.
Заполните пустые клетки в решении уравнения
5x2-7x+2 = 0
5x2-5x-[ ]+2 = 0
5x([ ]-1)-2(x-[ ]) = 0
([ ]-[ ]) (5x-2) =
[ ] - [ ] =0 5x-2 = 0
Дорешайте полученные уравнения.
Решите по образцу:
x2+6x-7 = 0
3x2+5x-2 = 0
x2-6x+5 = 0
Группа №3.
Решение уравнений выделением полного квадрата двучлена.
Инструкция.
Внимательно прочитайте пример решения уравнения x2+10x-24 = 0
Формула полного квадрата двучлена (a+b)2 = a2+2ab+b2
x2+10x-24 = x2+2*5x-24
Значит, в формуле a = x, b = 5. То есть на последнем месте должно быть 52 = 25
x2+10x-24 = x2+2*5x+25-25-24
Чтобы значение двучлена не изменилось, 25 прибавили и тут же вычли. Получаем x2+10x-24 = x2+2*5x+25-25-24 = x2+10x+25-49 = (x+5)2-49 = 0
(x-5)2-49 = 0
(x-5)2=49
(x-5)2 = 72
x-5 = 7 x-5 = -7 Решаем эти уравнения.
Заполните пустые клетки в решении уравнения.
x2+6x-7 = 0
x2+6x-7 = x2+2*[ ]*x-7 = x2+2*[ ]x +32-32-7 = x2+6x+9-9-7 = (x+3)2-16
(x+3)2-16 = 0
(x+3)2 = 16
(x+3) = [ ] (x+3) = [ ]
Дорешайте полученные уравнения.
Решите по образцу:
x2-6x+5 = 0
x2-2x-8 = 0
Группа №4.
Решение уравнений с использованием свойств коэффициентов квадратного уравнения.
Инструкция:
Решите уравнения:
x2+6x-7 = 0
x2-6x+5 = 0
5 x2-7x+2 = 0
3 x2-5x+2 = 0
2 x2+3x-5 = 0
Очень внимательно проанализируйте ответы.
Очень внимательно проанализируйте коэффициенты a, b, c.
Найдите связи, которые объединяют все уравнения.
Сделайте вывод и сформулируйте метод решения уравнений с таким свойством коэффициентов.
Группа №5.
Графическое решение уравнений.
Инструкция.
Решите графически уравнения:
x2-3x-4 = 0
x2-2x+1 = 0
x2-2x+5 = 0
Сделайте вывод о всех возможных случаях взаимного расположения параболы и прямой.
Сделайте вывод о возможном количестве корней уравнения.
После самостоятельной работы, представитель от группы представляет свой метод решения у доски, остальные ученики работают в своих тетрадях.
По окончании работы, руководитель группы оценивает деятельность своего коллектива. В соответствии с этим учитель оценивает работу всей группы отметкой в журнал.
V. Запись домашнего задания.
VI. Рефлексия. Каждый ученик кладёт на стол кружок со значком:
? – не понял
. – в целом, понял
! – понял всё. |
|
|
 Скачать 78.22 Kb.
Скачать 78.22 Kb.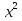 +bx+c=0, где a, b, c – числа, а ≠0, х – переменная.
+bx+c=0, где a, b, c – числа, а ≠0, х – переменная.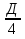 = (
= (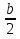 )2 - ac
)2 - ac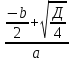 x2 =
x2 =