| Заборкин Купить забор из серого профнастила Заборкин. zaborkin.ru |
Урок по теме: «Таблица производных»
 Скачать 77.49 Kb. Скачать 77.49 Kb.
|
| Министерство образования России Муниципальное бюджетное образовательное учреждение Средняя общеобразовательная школа №19 Урок обобщающего повторения по теме: «Таблица производных» 11 класс Разработала учитель математики Склярова Г.В. г.Армавир 2015 Обобщающий урок по теме: «Таблица производных» ЦЕЛЬ: - обобщить и систематизировать материал по теме: повторить понятия производная, дифференцирование, сложная функция, алгоритм нахождения производной, правила дифференцирования; - развивать логическое мышление, монологическую речь в ходе объяснений, обоснований выполняемых действий, навыки самостоятельной и исследовательской работы. ПЛАН УРОКА: 1.Определение цели урока. 2.Что такое производная? Историческая справка. 3.Проверка домашнего задания (вычисление производных элементарных функций с помощью определения производной, правил дифференцирования, методов математической индукции – исследовательская работа). 4.Устный математический диктант. 5. Производная сложной функции (фронтальная работа). 6.Письменная работа (тест – задания ЕГЭ) 7.Подведение итогов работы – составление опорного конспекта. 8.Домашнее задание. На уроке используется мультимедийная установка, презентация «Производная» ХОД УРОКА: 1.Прочитайте тему урока. Какому слову вы бы отвели главное место? А как вы думаете чем мы будем заниматься на уроке? Кто попробует сформулировать тему и цель урока: - попробуем составить таблицу производных элементарных функций, - закрепить навыки в технике вычисления производной. 2. Составим план нашей работы. Давайте вспомним, какие мы с вами понятия изучали, рассматривая тему «Производная» (опорный конспект): - определение; - алгоритм нахождения производной; - правила дифференцирования; - таблица производных. Итак, мы начинаем нашу работу, в ходе которой вы должны заполнить опорную схему. 3. Что же такое производная? О происхождении терминов и обозначений производной и предела. Свое исследование по этому вопросу представляет ……(сведения из истории). Производная – одно из фундаментальных понятий математики. Оно возникло в 17 веке в связи с необходимостью решения ряда задач из физики, механики и математики. Независимо друг от друга И.Ньютон и Г.Лейбниц разработали аппарат, которым пользуемся ив настоящее время. И.Ньютон в основном опирался на физическое представление производной, а Г.Лейбниц использовал понятие бесконечно малой. Исчисление, созданное Ньютоном и Лейбницом, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии. В частности, с помощью методов дифференциального исчисления, ученые предсказали возвращение каметы Галлея, что было большим триумфом науки 18 века. Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале 19 века французский математик О.Коши дал строгое построение дифференциального исчисления на основе понятия предела. Применяемая сейчас система обозначений для производной восходит к Лейбницу и Лангранжу. В настоящее время понятие производной находит бльшое применение в различных областях науки и техники. Часто можно слышать, что математики и физики – это лирики. Софья Ковалевская говорила: «Математик должен быть поэтом в душе» Приведу слова из учительского фольклора «Алгоритм нахождения производной» (заполняем графу опорного конспекта). В данной функции от Х, нареченной игреком Вы фиксируете Х, отмечая индексом Придаете ему тот час приращение Те у функции самой, вызвав изменение. Приращений тех теперь, взявши отношение Пробуждаете к нулю у Х стремление Предел такого отношения вычисляете Он производною в науке называется. Проверим выполнение домашнего задания. Вычислить производные с помощью определения.
Решение:
(Заполняем соответствующую графу конспекта: (с)1=0, (кх+в)1=к. 4.Следующий этап нашей работы. Что такое дифференцирование? Вспомним правила дифференцирования. Основные формулы и следствия их них (ответы учеников с места). Устный математический диктант. Какие правила дифференцирования можно применить?
5.Продолжаем заполнять таблицу производных элементарных функций. Со своими исследованиями знакомит нас …. Вычислить производную степенной функции у=х3: А) с помошью определения производной; Б) с помощью правил дифференцирования; В) метод математической индукции. Метод математической индукции (Б. Паскаль, Я.Бернулли) Индукция – это переход от частного утверждения к общему. Алгоритм:
Заполняем опорную схему: производная степенной функции. Вычилить производну тригонометрической функции: у=sinх ( с помощью определения производной). 6. Следующий этап нашей работы. Поговорим о производной сложной функции. Сложная функция – это функция вида у=f(u(х)). У1=f1(u(х))=f1(u(х))u1(х) 7. Последний этап нашей работы. Проверим технику вашего дифференцирования. Письменная работа.
8.Подведение итогов работы (озвучивание опорной схемы учениками у доски). 9.Домашнее задание: составить и решить карточку «Прверь себя»- задание: найти производные функций по определению, с помощью таблицы производных и правил дифференцирования. Опорный конспект Определение производной:______________________________________________________________________________________________________________________________________________________________________________ Алгоритм нахождения производной ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Правила дифференцирования Основные формулы Следствия ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Таблица производных Элементарные функции Сложная функция __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ | ||||||||||||||||||||||||||||||||||||||||||||||||||
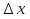 , f(х0+
, f(х0+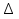 у=f(х0+
у=f(х0+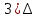 у=f(х0+
у=f(х0+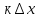 - кх0-в=
- кх0-в=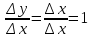
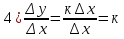
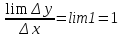
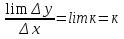
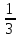 х3+
х3+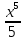 (АДЕ)
(АДЕ)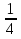 х4+
х4+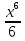 (АДЕ)
(АДЕ)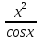 (В)
(В)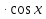 (Б)
(Б)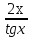 (ВД)
(ВД)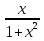 (АГДВ)
(АГДВ)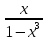 (АДВ)
(АДВ)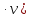 1=u1v+uv1
1=u1v+uv1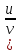 )1=
)1=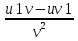
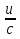 )1=
)1=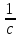 u1
u1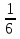 х4+
х4+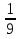 х3+
х3+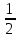 х2-х+7, х0=1
х2-х+7, х0=1